Đề thi học kì 1 Toán 7 - Đề số 7 - Chân trời sáng tạoTải vềPhần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm. Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
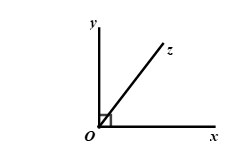
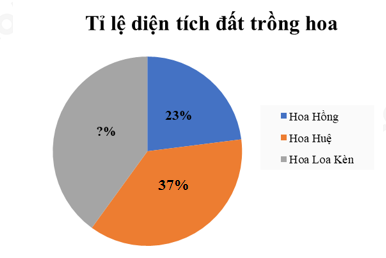
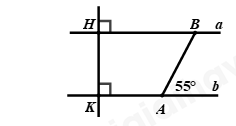
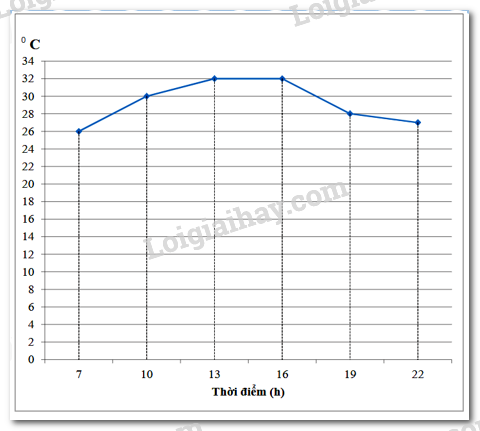
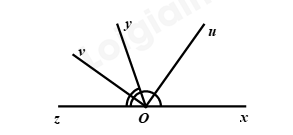
Đề bài Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm. Câu 1: Các số hữu tỉ \(\dfrac{{ - 5}}{{11}}\,\,;\,\,\dfrac{{ - 5}}{9}\,\,;\,\,\dfrac{7}{5}\,\,;\,\,\dfrac{3}{5}\,\,;\,\,\dfrac{{18}}{{13}}\) được sắp xếp theo thứ tự tăng dần là: A. \(\dfrac{{ - 5}}{{11}}\,\,;\,\,\dfrac{{ - 5}}{9}\,\,;\,\,\dfrac{{18}}{{13}}\,\,;\,\,\dfrac{7}{5}\,\,;\,\,\dfrac{3}{5}.\) B. \(\dfrac{{ - 5}}{9}\,\,;\,\,\dfrac{{ - 5}}{{11}}\,\,;\,\,\dfrac{3}{5}\,\,;\,\,\dfrac{{18}}{{13}}\,\,;\dfrac{7}{5}.\) C. \(\dfrac{{ - 5}}{{11}}\,\,;\,\,\dfrac{{ - 5}}{9}\,\,;\,\,\dfrac{3}{5}\,\,;\,\,\dfrac{{18}}{{13}}\,\,;\,\,\dfrac{7}{5}.\) D. \(\dfrac{{ - 5}}{9}\,\,;\,\,\dfrac{{ - 5}}{{11}}\,\,;\,\,\dfrac{3}{5}\,\,;\,\,\dfrac{7}{5}\,\,;\,\,\dfrac{{18}}{{13}}.\) Câu 2: Kết quả của phép tính: \(\dfrac{{{3^{10}}}}{{{5^{10}}}}{.5^{10}}\) là: A. \({3^5}\) B. \({3^{20}}\) C. \({3^{10}}\) D. \({5.3^{10}}\) Câu 3: Kết quả của phép tính: \(\sqrt {0,04} + \sqrt {0,25} + 2,31\) là: A. \(2,53\) B. \(2,96\) C. \(2,6\) D. \(3,01\) Câu 4: Cho \(x,y\) là hai số thực tùy ý. Khẳng định nào sau đây đúng? A. \(\left| {x - y} \right| = x - y\) B. \(\left| {x - y} \right| = \left| x \right| - \left| y \right|\) C. \(\left| {x + y} \right| = \left| x \right| + \left| y \right|\) D. \(\left| {x + y} \right| = \left| x \right| - \left| y \right|\) nếu \(x > 0 > y\) và \(\left| x \right| \ge \left| y \right|\) Câu 5: Quan sát hình vẽ bên dưới: Tính số đo góc \(xOz\), biết \(\dfrac{1}{5}\angle xOz = \dfrac{1}{4}\angle yOz\). A. \(\angle xOz = {40^0}\) B. \(\angle xOz = {50^0}\) C. \(\angle xOz = {30^0}\) D. \(\angle xOz = {60^0}\) Câu 6: Một cái hòm hình chữ nhật có chiều dài \(36\,cm,\) chiều rộng \(15\,cm,\) chiều cao \(16\,cm.\) Số hình lập phương cạnh \(3\,cm\) nhiều nhất chứa trong hòm đó là: A. \(180\) B. \(300\) C. \(320\) D. \(192\) Câu 7: Biểu đồ hình quạt dưới đây thể hiện diện tích đất trộng: hoa Huệ, hoa Hồng và hoa Loa kèn trong vườn hoa nhà cô Loan. Diện tích đất trồng hoa Loa kèn và hoa Hồng chiếm bao nhiêu phần trăm diện tích đất trồng hoa? A. \(23\% \) B. \(60\% \) C. \(40\% \) D. \(63\% \) Câu 8: Quan sát hình vẽ bên dưới, tính số đo góc \(\angle ABH\) biết \(a//b\). A. \(\angle ABH = {125^0}\) B. \(\angle ABH = {65^0}\) C. \(\angle ABH = {55^0}\) D. \(\angle ABH = {95^0}\) Câu 9: Điền cụm từ còn thiếu vào …: “Định lí …” A. là một khẳng định được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … thì …. B. là một câu nói được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … thì …. C. là một khẳng định được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … vậy…. D. là một câu nói được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … vậy …. Câu 10: Biểu đồ đoạn thẳng trên cho biết nhiệt độ ở Hà Nội trong ngày 07/05/2021 tại một số thời điểm. Hãy cho biết thời điểm nào nhiệt độ thấp nhất, cao nhất?
A. Thời điểm nhiệt độ thấp nhất là 26 độ C; thời điểm nhiệt độ cao nhất là 32 độ C. B. Thời điểm nhiệt độ thấp nhất là 22 độ C; thời điểm nhiệt độ cao nhất là 32 độ C C. Thời điểm nhiệt độ thấp nhất là 22 giờ; thời điểm nhiệt độ cao nhất là 13 giờ đến 16 giờ. D. Thời điểm nhiệt độ thấp nhất là 7 giờ; thời điểm nhiệt độ cao nhất là 13 giờ đến 16 giờ.
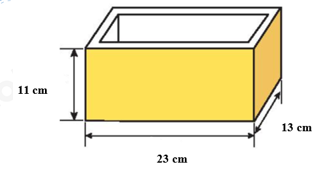
Phần II. Tự luận (7 điểm): Bài 1: (2,0 điểm) Thực hiện phép tính: a) \(3,5.\dfrac{2}{{21}} - \dfrac{5}{9}:\dfrac{{25}}{3} + \dfrac{1}{{15}}\) b) \(16.{\left( {\dfrac{3}{{20}} - \dfrac{2}{5}} \right)^2} + \dfrac{3}{5}\) c) \(\dfrac{{ - 11}}{3}:\left( {1,5.\sqrt {\dfrac{{16}}{9}} - \dfrac{{10}}{3}} \right)\) d) \(\left( {\sqrt {\dfrac{{81}}{{16}}} + \dfrac{{ - 3}}{4}} \right):{\left( { - \dfrac{3}{4}} \right)^2} - \left| {\dfrac{{ - 27}}{4}:{3^2}} \right|\) Bài 2: ( 2 điểm) Tìm \(x\), biết: a) \(\dfrac{1}{3}:x = 2\dfrac{2}{3}:\left( { - 0,3} \right)\) b) \({3^{2x}} - {2.3^5} = {3^5}\) c) \(2x - \sqrt {1,69} = \sqrt {1,21} \) d) \(\left| {x + \dfrac{1}{3}} \right|.\left( {{x^2} + 1} \right) = 0\) Bài 3: (1 điểm) Cho góc vuông \(uOv\) và tia \(Oy\) đi qua một điểm trong của góc đó. Vẽ tia \(Ox\) sao cho \(Ou\) là tia phân giác của góc \(xOy\). Vẽ tia \(Oz\) sao cho \(Ov\) là tia phân giác của góc \(yOz\). Chứng minh rằng hai góc \(xOy\) và \(yOz\) là hai góc kề bù. Bài 4: (1,5 điểm) Một khuôn đúc bê tông có kích thước như hình vẽ. Bề dày các mặt bên của khuôn là \(1,2\,cm.\) Bề dày mặt đáy của khuôn là \(1,9\,cm.\) Thể tích của khối bê tông được khuôn này đúc ra là bao nhiêu xăngtimét khối? Bài 5 (0,5 điểm): Tìm giá trị lớn nhất của biểu thức: \(A = - \sqrt {{x^2} + 81} + 2030.\) Lời giải Phần I: Trắc nghiệm
Câu 1 Phương pháp: Quy đồng các phân số cùng mẫu dương để so sánh. Cách giải: *Ta có: \(11 < 9\), do đó, \(\dfrac{5}{{11}} < \dfrac{5}{9}\) suy ra \(\dfrac{{ - 5}}{{11}} > \dfrac{{ - 5}}{9}\) *Ta có: \(\dfrac{7}{5} = \dfrac{{91}}{{65}}\,\,;\,\,\dfrac{3}{5} = \dfrac{{39}}{{65}}\,\,;\,\,\dfrac{{18}}{{13}} = \dfrac{{90}}{{65}}\) Vì \(39 < 90 < 91\) nên \(\dfrac{{39}}{{65}} < \dfrac{{90}}{{65}} < \dfrac{{91}}{{65}}\) hay \(\dfrac{3}{5} < \dfrac{{18}}{{13}} < \dfrac{7}{5}\) Thứ tự tăng dần của các số hữu tỉ là: \(\dfrac{{ - 5}}{{11}}\,\,;\,\,\dfrac{{ - 5}}{9}\,\,;\,\,\dfrac{3}{5}\,\,;\,\,\dfrac{{18}}{{13}}\,\,;\,\,\dfrac{7}{5}.\) Chọn C. Câu 2 Phương pháp: Vận dụng công thức tính lũy thừa của một thường bằng thương các lũy thừa: \({\left( {\dfrac{x}{y}} \right)^n} = \dfrac{{{x^n}}}{{{y^n}}}\,\left( {y \ne 0} \right)\) Cách giải: \({\left( {\dfrac{3}{5}} \right)^{10}}:{5^{10}}\)\( = \dfrac{{{3^{10}}}}{{{5^{10}}}}{.5^{10}} = {3^{10}}\) Chọn C. Câu 3 Phương pháp: Thực hiện tính căn bậc hai. Cách giải: \(\begin{array}{l}\,\,\,\,\sqrt {0,04} + \sqrt {0,25} + 2,31\\ = 0,2 + 0,5 + 2,31\\ = 0,7 + 2,31\\ = 3,01\end{array}\) Chọn D. Câu 4 Phương pháp: Vận dụng kiến thức về dấu giá trị tuyệt đối của một số. Cách giải: + Đáp án A sai, khi \(x < y\) + Đáp án B sai, lấy ví dụ khi \(x = 0;y \ne 0\) + Đáp án C sai, lấy ví dụ khi \(x = - y \ne 0\) + Đáp án D đúng, theo quy tắc cộng hai số trái dấu. Chọn D. Câu 5 Phương pháp: Từ giả thiết của bài toán: \(\dfrac{1}{5}\angle xOz = \dfrac{1}{4}\angle yOz\), tìm được \(\angle yOz\) theo \(\angle xOz\) Vì hai góc \(xOz\) và \(yOz\) là hai góc kề nhau nên \(\angle xOy = \angle xOz + \angle yOz\) Từ đó tính được \(\angle xOz\) Cách giải: Ta có: \(\dfrac{1}{5}\angle xOz = \dfrac{1}{4}\angle yOz\) suy ra \(\angle yOz = \dfrac{4}{5}\angle xOz\) Vì hai góc \(xOz\) và \(yOz\) là hai góc kề nhau nên \(\angle xOy = \angle xOz + \angle yOz = {90^0}\) \(\begin{array}{l} \Rightarrow \angle xOz + \dfrac{4}{5}\angle xOz = {90^0}\\ \Rightarrow \left( {1 + \dfrac{4}{5}} \right).\angle xOz = {90^0}\\ \Rightarrow \dfrac{9}{5}.\angle xOz = {90^0}\\ \Rightarrow \angle xOz = {90^0}:\dfrac{9}{5} = {90^0}.\dfrac{5}{9}\\ \Rightarrow \angle xOz = {50^0}\end{array}\) Vậy \(\angle xOz = {50^0}\) Chọn B. Câu 6 Phương pháp: Bước 1: Tính xem chiều dài chia được bao nhiêu đoạn \(3cm\) Bước 2: Tính xem chiều rộng chia được bao nhiêu đoạn \(3cm\) Bước 3: Tính xem chiều cao chia được bao nhiêu đoạn \(3cm\) Bước 4: Tính số hình lập phương cạnh \(3cm\) mà hòm chứa được Cách giải: Ta thấy: \(36:3 = 12; & 15:3 = 5: & 16:3 = 5\dfrac{1}{3}\) Số khối lập phương cạnh \(3cm\) mà hòm có thể chứa được là: \(12.5.5 = 300\,\)(khối) Chọn B. Câu 7 Phương pháp: Đọc và mô tả biểu đồ hình quạt. Thực hiện phép cộng để tính. Cách giải: Từ biểu đồ hình quạt, ta thấy diện tích đất trồng hoa Hồng chiếm 23%; diện tích đất trồng hoa Huệ chiếm 37%. Diện tích đất trồng hoa Loa kèn chiếm số phần trăm là: \(100\% - 23\% - 37\% = 40\% \) Diện tích đất trong hoa Loa kèn và hoa Hồng chiếm số phần trăm diện tích đất trồng hoa là: \(40\% + 23\% = 63\% \) (diện tích đất trồng hoa) Chọn D. Câu 8 Phương pháp: Vận dụng tính chất của hai đường thẳng song song: Hai đường thẳng song song thì hai góc ở vị trí so le trong bằng nhau. Cách giải: Ta có: \(a//b\) (giả thiết) nên \(\angle BAb = \angle ABH = {55^0}\) (hai góc so le trong) Vậy \(\angle ABH = {55^0}\) Chọn C. Câu 9 Phương pháp: Định lí là một khẳng định được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … thì …. Cách giải: Định lí là một khẳng định được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … thì …. Chọn A. Câu 10 Phương pháp: Phân tích dữ liệu biểu đồ đoạn thẳng. Cách giải: Từ biểu đồ đoạn thẳng, ta thấy: Thời điểm nhiệt độ thấp nhất là 7 giờ; thời điểm nhiệt độ cao nhất là 13 giờ đến 16 giờ. Chọn A.
Phần II. Tự luận: Bài 1 Phương pháp: a) Thực hiện phép cộng, trừ, nhân, chia với các số hữu tỉ. b) Tính lũy thừa của một số hữu tỉ: \({\left( {\dfrac{a}{b}} \right)^n} = \dfrac{{{a^n}}}{{{b^n}}}\,\,\left( {b \ne 0;n \in \mathbb{Z}} \right)\) Thực hiện phép cộng, trừ, nhân với các số hữu tỉ. c) Tính căn bậc hai số học. Thực hiện phép trừ, chia với các số hữu tỉ. d) Tính căn bậc hai số học, tính lũy thừa của một số hữu tỉ: \({\left( {\dfrac{a}{b}} \right)^n} = \dfrac{{{a^n}}}{{{b^n}}}\,\,\left( {b \ne 0;n \in \mathbb{Z}} \right)\), tính giá trị tuyệt đối của một số. Cách giải: a) \(3,5.\dfrac{2}{{21}} - \dfrac{5}{9}:\dfrac{{25}}{3} + \dfrac{1}{{15}}\) \(\begin{array}{l} = \dfrac{7}{2}.\dfrac{2}{{21}} - \dfrac{5}{9}.\dfrac{3}{{25}} + \dfrac{1}{{15}}\\ = \dfrac{1}{3} - \dfrac{1}{{15}} + \dfrac{1}{{15}}\\ = \dfrac{1}{3} + \left( { - \dfrac{1}{{15}} + \dfrac{1}{{15}}} \right)\\ = \dfrac{1}{3} + 0 = \dfrac{1}{3}\end{array}\) b) \(16.{\left( {\dfrac{3}{{20}} - \dfrac{2}{5}} \right)^2} + \dfrac{3}{5}\) \(\begin{array}{l} = 16.{\left( {\dfrac{3}{{20}} - \dfrac{8}{{20}}} \right)^2} + \dfrac{3}{5}\\ = 16.{\left( {\dfrac{{ - 5}}{{20}}} \right)^2} + \dfrac{3}{5}\\ = 16.{\left( {\dfrac{{ - 1}}{4}} \right)^2} + \dfrac{3}{5}\\ = 16.\dfrac{{{{\left( { - 1} \right)}^2}}}{{{4^2}}} + \dfrac{3}{5}\\ = 16.\dfrac{1}{{16}} + \dfrac{3}{5}\\ = 1 + \dfrac{3}{5} = \dfrac{5}{5} + \dfrac{3}{5}\\ = \dfrac{8}{5}\end{array}\) c) \(\dfrac{{ - 11}}{3}:\left( {1,5.\sqrt {\dfrac{{16}}{9}} - \dfrac{{10}}{3}} \right)\) \(\begin{array}{l} = \dfrac{{ - 11}}{3}:\left( {\dfrac{3}{2}.\dfrac{4}{3} - \dfrac{{10}}{3}} \right)\\ = \dfrac{{ - 11}}{3}:\left( {\dfrac{6}{3} - \dfrac{{10}}{3}} \right)\\ = \dfrac{{ - 11}}{3}:\dfrac{{ - 4}}{3}\\ = \dfrac{{ - 11}}{3}.\dfrac{3}{{ - 4}}\\ = \dfrac{{11}}{4}\end{array}\) d) \(\left( {\sqrt {\dfrac{{81}}{{16}}} + \dfrac{{ - 3}}{4}} \right):{\left( { - \dfrac{3}{4}} \right)^2} - \left| {\dfrac{{ - 27}}{4}:{3^2}} \right|\) \(\begin{array}{l} = \left( {\dfrac{9}{4} + \dfrac{{ - 3}}{4}} \right):\dfrac{{{{\left( { - 3} \right)}^2}}}{{{4^2}}} - \left| {\dfrac{{ - 27}}{4}.\dfrac{1}{{{3^2}}}} \right|\\ = \dfrac{6}{4}:\dfrac{9}{{16}} - \left| {\dfrac{{ - 27}}{4}.\dfrac{1}{9}} \right|\\ = \dfrac{6}{4}.\dfrac{{16}}{9} - \left| {\dfrac{{ - 3}}{4}} \right|\\ = \dfrac{8}{3} - \left[ { - \left( { - \dfrac{3}{4}} \right)} \right]\\ = \dfrac{8}{3} - \dfrac{3}{4} = \dfrac{{32}}{{12}} - \dfrac{9}{{12}}\\ = \dfrac{{23}}{{12}}\end{array}\) Bài 2 Phương pháp: a) Thực hiện phép nhân, chia các số hữu tỉ tìm \(x\). b) Giải \({a^{f\left( x \right)}} = {a^{g\left( x \right)}} \Rightarrow f\left( x \right) = g\left( x \right)\) c) Tính căn bậc hai số học, vận dụng quy tắc chuyển vế tìm \(x\). d) Giải \(A\left( x \right).B\left( x \right) = 0\) Trường hợp 1: Giải \(A\left( x \right) = 0\) Trường hợp 2: Giải \(B\left( x \right) = 0\) \(\left| {A\left( x \right)} \right| = 0\) suy ra \(A\left( x \right) = 0\) Cách giải: a) \(\dfrac{1}{3}:x = 2\dfrac{2}{3}:\left( { - 0,3} \right)\) \(\begin{array}{l}\dfrac{1}{3}:x = \dfrac{8}{3}:\dfrac{{ - 3}}{{10}}\\\dfrac{1}{3}:x = \dfrac{8}{3}.\dfrac{{10}}{{ - 3}}\\\dfrac{1}{3}:x = \dfrac{{80}}{{ - 9}}\\x = \dfrac{1}{3}:\dfrac{{80}}{{ - 9}} = \dfrac{1}{3}.\dfrac{{ - 9}}{{80}}\\x = \dfrac{{ - 3}}{{80}}\end{array}\) Vậy \(x = \dfrac{{ - 3}}{{80}}\) b) \({3^{2x}} - {2.3^5} = {3^5}\) \(\begin{array}{l}{3^{2x}} = {3^5} + {2.3^5}\\{3^{2x}} = \left( {1 + 2} \right){.3^5}\\{3^{2x}} = {3.3^5} = {3^1}{.3^5}\\{3^{2x}} = {3^{1 + 5}}\\{3^{2x}} = {3^6}\\ \Rightarrow 2x = 6\\\,\,\,\,\,\,\,\,\,\,x = 6:2\\\,\,\,\,\,\,\,\,\,\,x = 3\end{array}\) Vậy \(x = 3\) c) \(2x - \sqrt {1,69} = \sqrt {1,21} \) \(\begin{array}{l}2x - 1,3 = 1,1\\2x = 1,1 + 1,3\\2x = 2,4\\x = 2,4:2\\x = 1,2\end{array}\) Vậy \(x = 1,2\) d) \(\left| {x + \dfrac{1}{3}} \right|.\left( {{x^2} + 1} \right) = 0\) Trường hợp 1: \(\begin{array}{l}\left| {x + \dfrac{1}{3}} \right| = 0\\x + \dfrac{1}{3} = 0\\x = \dfrac{{ - 1}}{3}\end{array}\) Trường hợp 2: \({x^2} + 1 = 0\) Vì \({x^2} \ge 0\) với mọi \(x\) nên \({x^2} + 1 \ge 1 > 0\) với mọi \(x\) Do đó, không có \(x\) thỏa mãn \({x^2} + 1 = 0\) Vậy \(x = - \dfrac{1}{3}\) Bài 3 Phương pháp: Vận dụng tính chất tia phân giác của một góc Dấu hiệu nhận biết hai góc kề bù Cách giải: Vì \(Ou\) là tia phân giác của \(\angle xOy\) nên \(\angle xOy = 2\angle uOy\) (tính chất tia phân giác của một góc) \(Ov\) là tia phân giác của \(\angle yOz\) nên \(\angle yOz = 2\angle yOv\) (tính chất tia phân giác của một góc) Ta có: \(\angle xOy + \angle yOz = 2\angle uOy + 2\angle yOv\) \(\begin{array}{l} = 2.\left( {\angle uOy + \angle yOv} \right)\\ = 2.\angle uOv\\ = {2.90^0} = {180^0}\end{array}\) Do đó, hai góc \(xOy\) và \(yOz\) là hai góc kề bù. Bài 4 Phương pháp: Áp dụng công thức tính thể tích của hình hộp chữ nhật \(V = a.b.c\) (trong đó \(a,\,b\) là các cạnh của đáy, \(c\) là chiều cao hình hộp chữ nhật) Bước 1: Tính chiều dài, chiều rộng và chiều cao của khuôn Bước 2: Tính thể tích khối bê tông đúc được Cách giải:
Phần bên trong khuôn có: + Chiều dài bằng: \(23 - 2.1,2 = 20,6\left( {cm} \right)\) + Chiều rộng là: \(13 - 2.1,2 = 10,6\left( {cm} \right)\) + Chiều cao là: \(11 - 1,9 = 9,1\left( {cm} \right)\) Thể tích của khuôn đúc là: \({V_1} = 20,6.10,6.9,1 = 1987,076\left( {c{m^3}} \right)\) Bài 5 Phương pháp: Vận dụng kiến thức lũy thừa của một số và căn bậc hai số học của một số. Cách giải: Ta có: \({x^2} \ge 0\) với mọi số thực \(x\) nên \({x^2} + 81 \ge 81\) với mọi số thực \(x\). Suy ra \(\sqrt {{x^2} + 81} \ge \sqrt {81} = 9\) với mọi số thực \(x\). Do đó, \( - \sqrt {{x^2} + 81} \le - 9\) với mọi số thực \(x\). Suy ra \(A = - \sqrt {{x^2} + 81} + 2030 \le - 9 + 2030\) hay \(A \le 2021\) với mọi số thực \(x\). Vậy giá trị lớn nhất của \(A\) là \(2021\). Dấu “=” xảy ra khi và chỉ khi \( \Leftrightarrow {x^2} = 0 \Leftrightarrow x = 0\).
|




















Danh sách bình luận