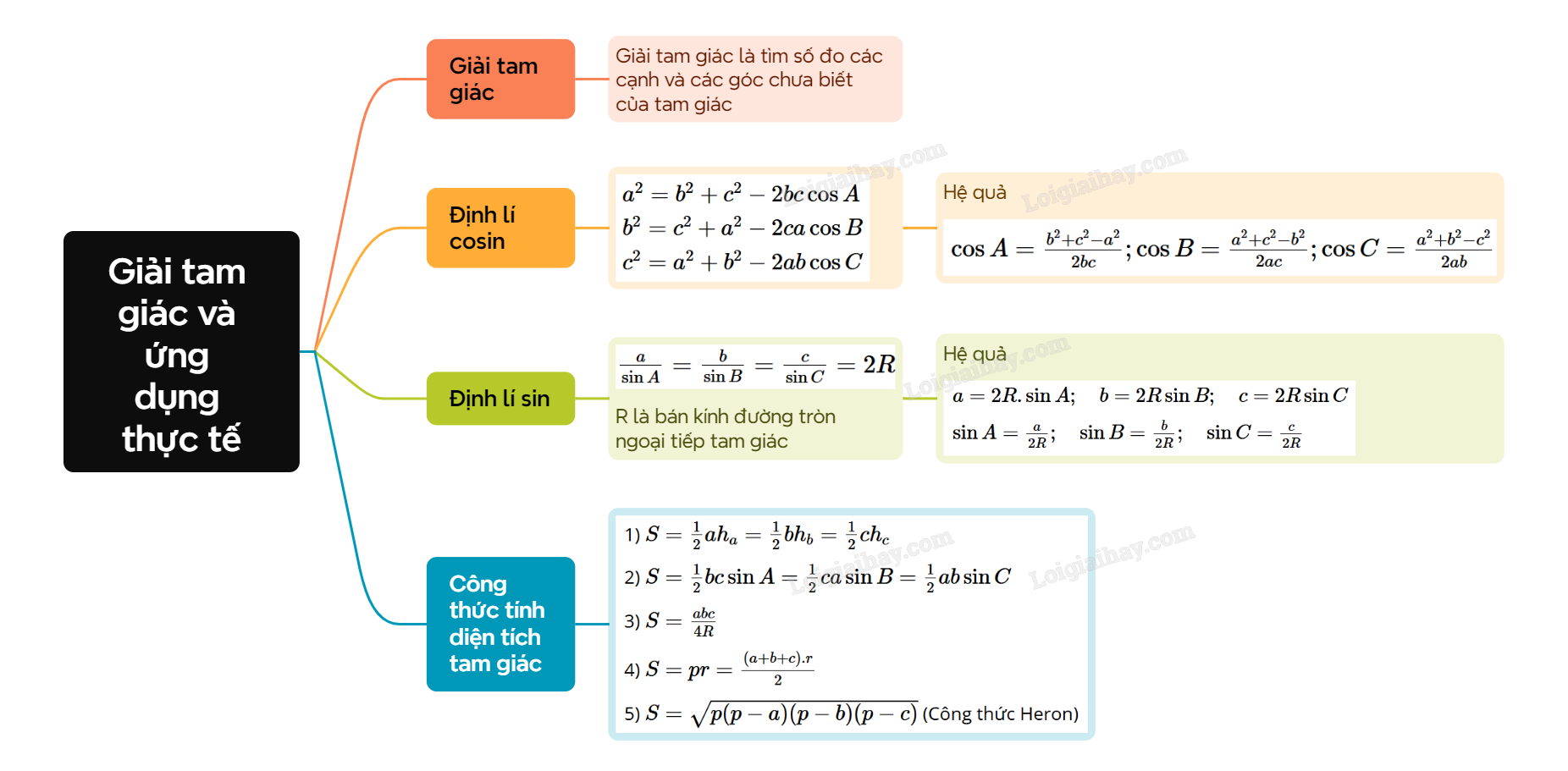
Lý thuyết Giải tam giác và ứng dụng thực tếGiải tam giác là tìm số đo các cạnh và các góc chưa biết của tam giác. Quảng cáo
Giải tam giác là tìm số đo các cạnh và các góc chưa biết của tam giác. 1. Định lí cosin Trong tam giác ABC: \({a^2} = {b^2} + {c^2} - 2bc\cos A\); \({b^2} = {c^2} + {a^2} - 2ca\cos B\); \({c^2} = {a^2} + {b^2} - 2ab\cos C\). Hệ quả: \(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\); \(\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\); \(\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}\). 2. Định lí sin Trong tam giác ABC: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\). (R là bán kính đường tròn ngoại tiếp tam giác ABC) Hệ quả \(a = 2R.\sin A\); \(b = 2R\sin B\); \( c = 2R\sin C\). \(\sin A = \frac{a}{{2R}}\); \(\sin B = \frac{b}{{2R}}\); \(\sin C = \frac{c}{{2R}}\). 3. Các công thức tính diện tích tam giác 1) \(S = \frac{1}{2}a{h_a} = \frac{1}{2}b{h_b} = \frac{1}{2}c{h_c}\). 2) \(S = \frac{1}{2}bc\sin A = \frac{1}{2}ca\sin B = \frac{1}{2}ab\sin C\). 3) \(S = \frac{{abc}}{{4R}}\). 4) \(S = pr = \frac{{(a + b + c).r}}{2}\). 5) \(S = \sqrt {p(p - a)(p - b)(p - c)} \) (Công thức Heron).
|




















Danh sách bình luận