Giải mục 3 trang 84, 85 SGK Toán 10 tập 1 - Chân trời sáng tạo

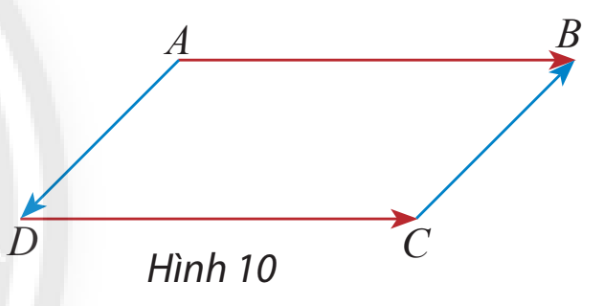
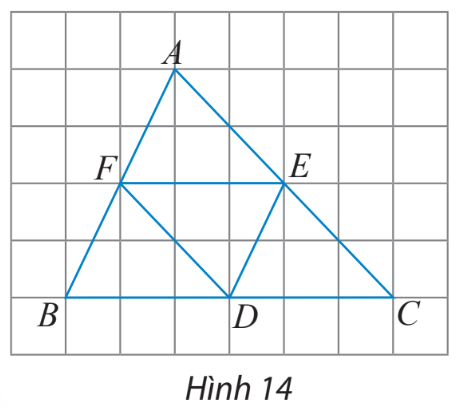
HĐ Khám phá 3

Cho hình bình hành ABCD (hình 30), hãy so sánh độ dài và hướng của hai vectơ :

a) $\overrightarrow {AB}$ và $\overrightarrow {DC}$

b) $\overrightarrow {AD}$ và $\overrightarrow {CB}$

Lời giải chi tiết:

a) Ta có: $AB = CD \Rightarrow \left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {CD} } \right|$

$AB//CD$ và $\overrightarrow {AB}$, $\overrightarrow {DC}$ có hướng từ trái sang phải

Suy ra $\overrightarrow {AB}$ và $\overrightarrow {DC}$ cùng hướng

b) Ta có: $AD = CB \Rightarrow \left| {\overrightarrow {AD} } \right| = \left| {\overrightarrow {CB} } \right|$

$AD//CB$ và $\overrightarrow {AD}$có hướng từ trên xuống dưới, $\overrightarrow {CB}$ có hướng từ dưới lên trên. Suy ra $\overrightarrow {AD}$ và $\overrightarrow {CB}$ngược hướng

Thực hành 5

Cho D, E, F lần lượt là trung điểm của cạnh BC, CA, AB của tam giác ABC (hình 14).

a) Tìm các vectơ bằng vectơ $\overrightarrow {EF}$.

b) Tìm các vectơ đối vectơ $\overrightarrow {EC}$

Phương pháp giải:

a)      

Bước 1: Từ H14, xác định các đoạn thẳng có độ dài bằng độ dài vectơ $\overrightarrow {EF}$

Bước 2: Trong đó liệt kê các vectơ cùng hướng với vectơ $\overrightarrow {EF}$

b)

Bước 1: Từ H14, xác định các đoạn thẳng có độ dài bằng độ dài vectơ $\overrightarrow {EC}$

Bước 2: Trong đó liệt kê các vectơ ngược hướng với vectơ $\overrightarrow {EC}$

Lời giải chi tiết:

Từ giả thiết ta có:

$AF = FB = ED$; $AE = EC = FD$; $BD = DC = EF$

Từ đó dựa vào hình ta có:

a) Các vectơ bằng vectơ $\overrightarrow {EF}$là $\overrightarrow {DB}$ và $\overrightarrow {CD}$

b) Các vectơ đối vectơ $\overrightarrow {EC}$ là $\overrightarrow {EA}$ và $\overrightarrow {DF}$