Giải mục 2 trang 96 SGK Toán 10 tập 1 - Chân trời sáng tạo

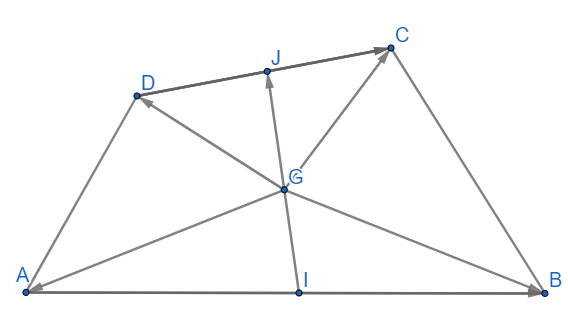
HĐ Khám phá 2

Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương khác \(\overrightarrow 0 \) và cho \(\overrightarrow c  = \frac{{\left| {\overrightarrow a } \right|}}{{\left| {\overrightarrow b } \right|}}.\overrightarrow b \). So sánh độ dài và hướng của hai vectơ \(\overrightarrow a \) và \(\overrightarrow c \)

Lời giải chi tiết:

\(\)vectơ \(\overrightarrow c  = \frac{{\left| {\overrightarrow a } \right|}}{{\left| {\overrightarrow b } \right|}}.\overrightarrow b \) có độ dài gấp \(\frac{{\left| {\overrightarrow a } \right|}}{{\left| {\overrightarrow b } \right|}}\) lần vectơ \(\overrightarrow b \) và cùng hướng với vectơ \(\overrightarrow b \)

+) Nếu hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng thì hai vectơ \(\overrightarrow a \) và \(\overrightarrow c \)cùng hướng và ngược lại

+) \(\left| {\overrightarrow c } \right| = \left| {\frac{{\left| {\overrightarrow a } \right|}}{{\left| {\overrightarrow b } \right|}}.\overrightarrow b } \right| = \frac{{\left| {\overrightarrow a } \right|}}{{\left| {\overrightarrow b } \right|}}.\left| {\overrightarrow b } \right| = \left| {\overrightarrow a } \right|\). Suy ra hai vectơ \(\overrightarrow a \) và \(\overrightarrow c \)có cùng độ dài

Thực hành 3

Cho tứ giác ABCD có I và J lần lượt là trung điểm của AB và CD. Cho điểm G thỏa mãn \(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD}  = \overrightarrow 0 \). Chứng minh ba điểm I, G, J  thẳng hàng

Phương pháp giải:

Sử dụng tính chất trung điểm và quy tắc ba điểm

\(\overrightarrow {GA}  + \overrightarrow {GB}  = 2\overrightarrow {GI} \) với I là trung điểm AB

\(\overrightarrow {GI}  + \overrightarrow {GJ}  = \overrightarrow 0 \Leftrightarrow\)  G là trung điểm IJ.

Lời giải chi tiết:

Ta có:

\(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD}  = \overrightarrow 0  \Leftrightarrow \left( {\overrightarrow {GI}  + \overrightarrow {IA} } \right) + \left( {\overrightarrow {GI}  + \overrightarrow {IB} } \right) + \left( {\overrightarrow {GJ}  + \overrightarrow {JC} } \right) + \left( {\overrightarrow {GJ}  + \overrightarrow {JD} } \right) = \overrightarrow 0 \)

\( \Leftrightarrow 2\overrightarrow {GI}  + \left( {\overrightarrow {IA}  + \overrightarrow {IB} } \right) + 2\overrightarrow {GJ}  + \left( {\overrightarrow {JC}  + \overrightarrow {JD} } \right) = \overrightarrow 0 \)

\( \Leftrightarrow 2\overrightarrow {GI}  + 2\overrightarrow {GJ}  = \overrightarrow 0  \Leftrightarrow 2\left( {\overrightarrow {GI}  + \overrightarrow {GJ} } \right) = \overrightarrow 0 \)

\( \Leftrightarrow \overrightarrow {GI}  + \overrightarrow {GJ}  = \overrightarrow 0  \Rightarrow \)G là trung điểm của đoạn thẳng IJ

Vậy I, G, J thẳng hàng