Giải mục 1 trang 33, 34 SGK Toán 10 tập 1 - Chân trời sáng tạo

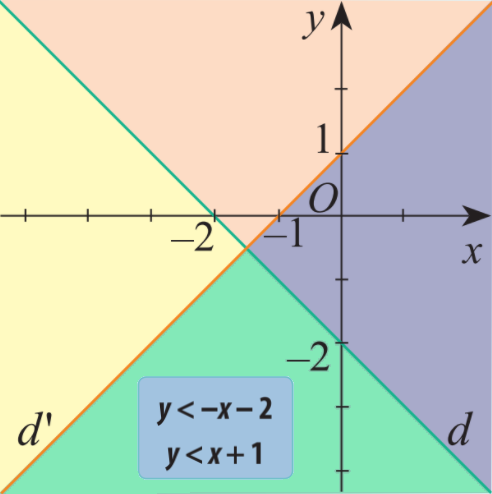
HĐ Khởi động

Lời giải chi tiết:

Vì \(0 >  - 0 - 2\) nên điểm O(0;0) không thuộc miền nghiệm của bất phương trình \(y <  - x - 2\)

Miền nghiệm của BPT \(y <  - x - 2\) là miền được tô màu vàng và xanh.

Vì \(0 < 0 + 1\) nên điểm O(0;0) thuộc miền nghiệm của bất phương trình \(y < x + 1\)

Miền nghiệm của BPT \(y < x + 1\) là miền được tô màu xanh và tím.

Vậy miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}y <  - x - 2\\y < x + 1\end{array} \right.\) là miền màu xanh (không kể các bờ d, d’)

Nói cách khác nhãn đã cho là nhãn của miền màu xanh.

HĐ Khám phá 1

Một người nông dân dự định quy hoạch x sào đất trồng cà tím và y sào đất trồng cà chua.

Biết rằng người đó chỉ có tối đa 9 triệu đồng để mua hạt giống và giá tiền hạt giống cho mỗi sào đất trồng cà tím là 200 000 đồng, mỗi sào đất trồng cà chua là 100 000 đồng.

a) Viết các bất phương trình mô tả các điều kiện ràng buộc đối với x, y.

b) Cặp số nào sau đây thỏa mãn đồng thời tất cả các bất phương trình nêu trên?

(20; 40),            (40; 20),          (-30; 10).

Lời giải chi tiết:

a)

Để quy hoạch x sào đất trồng cà tím, cần \(200\,000.x\)(đồng)

Để quy hoạch y sào đất trồng cà chua, cần \(100\,000.y\)(đồng)

Tổng số tiền để mua hạt giống là \(200{\rm{ }}000.x + 100{\rm{ }}000.y\) (đồng), tối đa là 9 triệu đồng nên ta có bất phương trình: \(0,2x + 0,1y \le 9\)

Ngoài ra số sào đất là số không âm nên \(x \ge 0\) và \(y \ge 0\)

b) + Cặp số (20; 40) thỏa mãn cả 3 bất phương trình trên vì \(0,2.20 + 0,1.40 = 8 < 9\).

+ Cặp số (40; 20) không thỏa mãn các bất phương trình trên vì \(0,2.40 + 0,1.20 = 10 > 9\).

+ Cặp số (-30; 10) không thỏa mãn các bất phương trình trên vì \( - 30 < 0\).

Thực hành 1

Hãy chỉ ra hai nghiệm của mỗi hệ bất phương trình trong Ví dụ 1.

Lời giải chi tiết:

a) \(\left\{ \begin{array}{l}3x + y - 1 \le 0\\2x - y + 2 \ge 0\end{array} \right.\)

Cặp số \((0;0)\) là một nghiệm của hệ bất phương trình trên vì \(\left\{ \begin{array}{l}3.0 + 0 - 1 =  - 1 \le 0\\2.0 - 0 + 2 = 2 \ge 0\end{array} \right.\)

Cặp số \((0; - 1)\) là một nghiệm của hệ bất phương trình trên vì \(\left\{ \begin{array}{l}3.0 + ( - 1) - 1 =  - 2 \le 0\\2.0 - ( - 1) + 2 = 3 \ge 0\end{array} \right.\)

c) \(\left\{ \begin{array}{l}y - 1 < 0\\x + 2 \ge 0\end{array} \right.\)

Cặp số \((0;0)\) là một nghiệm của hệ bất phương trình trên vì \(\left\{ \begin{array}{l}0 - 1 =  - 1 < 0\\0 + 2 = 2 \ge 0\end{array} \right.\)

Cặp số \((1;0)\) là một nghiệm của hệ bất phương trình trên vì \(\left\{ \begin{array}{l}0 - 1 =  - 1 < 0\\1 + 2 = 3 \ge 0\end{array} \right.\)

d) \(\left\{ \begin{array}{l}x + y - 3 \le 0\\ - 2x + y + 3 \ge 0\\x \ge 0\\y \ge 0\end{array} \right.\)

Cặp số \((0;0)\) là một nghiệm của hệ bất phương trình trên vì \(\left\{ \begin{array}{l}0 + 0 - 3 =  - 3 \le 0\\ - 2.0 + 0 + 3 = 3 \ge 0\\0 \ge 0\\0 \ge 0\end{array} \right.\)

Cặp số \((0;1)\) là một nghiệm của hệ bất phương trình trên vì \(\left\{ \begin{array}{l}0 + 1 - 3 =  - 2 \le 0\\ - 2.0 + 1 + 3 = 4 \ge 0\\0 \ge 0\\1 \ge 0\end{array} \right.\)