Đề kiểm tra 1 tiết chương 1: Dao động cơ - Đề số 03Đề bài
Câu 1 :
Phát biểu nào sau đây sai khi nói về chuyển động của con lắc lò xo:
Câu 2 :
Một con lắc đơn có chiều dài dây treo ℓ = 50 cm và vật nhỏ có khối lượng m = 0,01 kg mang điện tích q = +5.10-6 C được coi là điện tích điểm. Con lắc dao động điều hoà trong điện trường đều mà véctơ cường độ điện trường có độ lớn E = 104 V/m và hướng thẳng đứng xuống dưới. Lấy g = 10 m/s2; π = 3,14. Chu kì dao động điều hoà của con lắc là:
Câu 3 :
Pha của dao động được dùng để xác định
Câu 4 :
Một vật dao động điều hoà theo phương trình \(x = {\rm{ }}-5cos(5\pi t{\rm{ }} - 7\pi /6)cm\). Biên độ dao động và pha ban đầu của vật là:
Câu 5 :
Vật nặng dao động điều hòa với \(\omega = 10\sqrt 5 rad/s\). Chọn gốc tọa độ trùng với vị trí cân bằng của vật. Biết rằng tại thời điểm ban đầu vật đi qua li độ $x = 2cm$ với vận tốc \(v = 20\sqrt {15} cm/s\). Phương trình dao động của vật là:
Câu 6 :
Khi xảy ra hiện tượng cộng hưởng cơ thì vật tiếp tục dao động:
Câu 7 :
Một chất điểm dao động điều hòa với phương trình \(x = Acos(\omega t + \varphi )\). Biểu thức vận tốc tức thời của chất điểm là:
Câu 8 :
Khi xảy ra hiện tượng cộng hưởng thì:
Câu 9 :
Một vật dao động điều hòa với chu kỳ T và biên độ là A. Ban đầu vật ở vị trí cân bằng, khoảng thời gian ngắn nhất kể từ khi vật dao động đến thời điểm mà động năng bằng thế năng là:
Câu 10 :
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương cùng tần số. Biết dao động thứ nhất có biên độ \(A_1= 6 cm\) và trễ pha \(\dfrac{\pi}{2}\) so với dao động tổng hợp. Tại thời điểm dao động thứ hai có li độ bằng biên độ của dao động thứ nhất thì dao động tổng hợp có li độ \(9 cm\). Biên độ dao động tổng hợp bằng:
Câu 11 :
Một con lắc lò xo dao động điều hòa gồm lò xo có độ cứng k và vật có khối lượng m. Khi k = k1 thì chu kì dao động của con lắc là T1, khi k = k2 thì chu kì dao động của con lắc là T2. Khi mắc song song k1 với k2 thì chu kì dao động của con lắc là:
Câu 12 :
Một chất điểm dao động điều hòa theo phương trình \(x = 4cos\left( {4\pi t + \dfrac{\pi }{2}} \right)cm\). Quãng đường vật đi được sau \(1s\) là:
Câu 13 :
Khi nói về dao động điều hoà của một vật, phát biểu nào sau đây đúng?
Câu 14 :
Một con lắc đơn dao động với phương trình \(s = 2cos\left( {2\pi t} \right)cm\) (t tính bằng giây). Tần số dao động của con lắc là:
Câu 15 :
Một vật dao động điều hòa với phương trình \(x = Acos\left( {\omega t + \varphi } \right)\). Tại thời điểm ban đầu \(t = 0\), vật ở vị trí \(x = - A\). Pha ban đầu của dao động là:
Câu 16 :
Tại một nơi xác định, chu kì dao động điều hòa của con lắc đơn tỉ lệ nghịch với:
Câu 17 :
Một con lắc đơn đang dao động điều hòa với biên độ góc bằng \(9,{6^0}\) dưới tác dụng của trọng lực. Ở thời điểm \({t_0}\), vật nhỏ của con lắc có li độ góc và li độ cong lần lượt là \(4,{8^0}\) và \(3,2\pi cm\). Lấy \(g{\rm{ }} = {\rm{ }}10{\rm{ }}m/{s^2}\). Tốc độ của vật ở thời điểm \({t_0}\) bằng:
Câu 18 :
Một con lắc lò xo đang dao động tắt dần, cơ năng ban đầu của nó là \(6J\). Sau bốn chu kì kể từ lúc bắt đầu dao động thì biên độ của nó giảm đi \(24\% \). Phần cơ năng của con lắc chuyển hóa thành nhiệt năng tính trung bình trong mỗi chu kì dao động của nó là:
Câu 19 :
Một vật thực hiện đồng thời hai dao động điều hòa cùng phương cùng tần số có phương trình lần lượt là: \({x_1} = {\rm{ }}{A_1}cos\left( {\omega t + {\varphi _1}} \right)\) và \({x_2} = {\rm{ }}{A_2}cos\left( {\omega t + {\varphi _2}} \right)\). Biên độ dao động A của vật được xác định bởi công thức nào sau đây?
Câu 20 :
Dao động tổng hợp của hai dao động điều hòa cùng phương, cùng tần số có phương trình li độ là \(x = 4cos\left( {2\pi t - \dfrac{\pi }{6}} \right)cm\). Biết dao động thứ nhất có phương trình li độ là \({x_1} = 3cos\left( {2\pi t + \dfrac{\pi }{3}} \right)\). Dao động thứ hai có phương trình li độ là:
Câu 21 :
Phát biểu nào sau đây là đúng?
Câu 22 :
Một vật dao động điều hòa với chu kỳ \(T\) và biên độ \(A\). Khoảng thời gian ngắn nhất vật đi từ vị trí có động năng bằng thế năng đến vị trí có động năng bằng 3 lần thế năng là?
Câu 23 :
Khi gắn vật có khối lượng \({m_1} = 3kg\) vào một lò xo có khối lượng không đáng kể, nó dao động với chu kì \({T_1} = 1,2s\). Khi gắn một vật khác có khối lượng \({m_2}\) vào lò xo trên nó dao động với chu kì \({T_2} = 0,6s\). Khối lượng \({m_2}\) bằng?
Câu 24 :
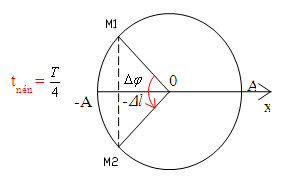
Một con lắc lò xo có độ cứng \(k = 160N/m\), đầu trên cố định còn đầu dưới gắn vật nặng \(m = 1,2kg\). Cho vật \(m\) dao động điều hòa theo phương thẳng đứng thì thấy thời gian lò xo nén trong một chu kì là \(0,14s\). Cho \(g = {\pi ^2} = 10m/{s^2}\). Biên độ dao động của vật là:
Câu 25 :
Hai con lắc lò xo giống nhau được treo vào hai điểm ở cùng độ cao, cách nhau \(4cm\). Kích thích cho hai con lắc dao động điều hòa theo phương thẳng đứng thì đồ thị biểu diễn sự phụ thuộc của li độ \(x\) vào thời gian \(t\) của hai vật như hình vẽ. Kể từ thời điểm \(t = 0\), hai vật cách nhau \(4\sqrt 3 cm\) lần thứ 2019 là 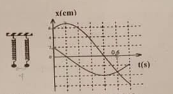
Lời giải và đáp án
Câu 1 :
Phát biểu nào sau đây sai khi nói về chuyển động của con lắc lò xo:
Đáp án : B Lời giải chi tiết :
A, C, D đúng B - sai vì gia tốc của vật luôn luôn thay đổi mà chuyển động biến đổi đều là chuyển động có gia tốc không đổi
Câu 2 :
Một con lắc đơn có chiều dài dây treo ℓ = 50 cm và vật nhỏ có khối lượng m = 0,01 kg mang điện tích q = +5.10-6 C được coi là điện tích điểm. Con lắc dao động điều hoà trong điện trường đều mà véctơ cường độ điện trường có độ lớn E = 104 V/m và hướng thẳng đứng xuống dưới. Lấy g = 10 m/s2; π = 3,14. Chu kì dao động điều hoà của con lắc là:
Đáp án : C Phương pháp giải :
+ Áp dụng công thức tính chu kì dao động của con lắc đơn: \(T = 2\pi \sqrt {\frac{l}{g}} \) + Áp dụng bài toán con lắc đơn chịu thêm tác dụng của lực điện Lời giải chi tiết :
Ta có, con lắc tích điện dương, cường độ điện trường \(\overrightarrow E \) hướng xuống => Lực điện \(\overrightarrow {{F_d}} \)hướng xuống Chu kì dao động của con lắc khi đó: \(T = 2\pi \sqrt {\frac{l}{{g'}}} \) Ta có: \(\begin{array}{l}g' = g + \frac{F}{m} = g + \frac{{\left| q \right|E}}{m} = 10 + \frac{{\left| {{{5.10}^{ - 6}}} \right|{{10}^4}}}{{0,01}} = 15m/{s^2}\\ \to T = 2\pi \sqrt {\frac{l}{{g'}}} = 2\pi \sqrt {\frac{{0,5}}{{15}}} = 1,147{\rm{s}}(s)\end{array}\) 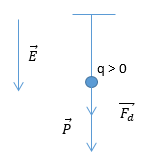
Câu 3 :
Pha của dao động được dùng để xác định
Đáp án : B Lời giải chi tiết :
\(\left( {\omega t + \varphi } \right)\) - Pha của dao động cho biết trạng thái dao động (gồm li độ \(x\) và chiều chuyển động \(\overrightarrow v \) )
Câu 4 :
Một vật dao động điều hoà theo phương trình \(x = {\rm{ }}-5cos(5\pi t{\rm{ }} - 7\pi /6)cm\). Biên độ dao động và pha ban đầu của vật là:
Đáp án : B Phương pháp giải :
+ Đồng nhất với phương trình dao động điều hòa: $x=Acos(ωt+φ)$ + Sử dụng công thức lượng giác: $-cosα=cos(α+π)$ + Vận dụng lí thuyết đại cương về các đại lượng trong phương trình dao động điều hòa. Lời giải chi tiết :
Ta có: $x = {\text{ }} - 5cos(5\pi t{\text{ }} - \frac{{7\pi }}{6}) = 5cos(5\pi t{\text{ }} - \frac{{7\pi }}{6} + \pi ) = 5cos(5\pi t{\text{ }} - \frac{\pi }{6})cm$ => Biên độ: $A=5 cm$, pha ban đầu: $\varphi = - \frac{\pi }{6}$
Câu 5 :
Vật nặng dao động điều hòa với \(\omega = 10\sqrt 5 rad/s\). Chọn gốc tọa độ trùng với vị trí cân bằng của vật. Biết rằng tại thời điểm ban đầu vật đi qua li độ $x = 2cm$ với vận tốc \(v = 20\sqrt {15} cm/s\). Phương trình dao động của vật là:
Đáp án : C Phương pháp giải :
- Sử dụng hệ thức độc lập xác định biên độ \({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}}\) - Xác định pha ban đầu: Tại $t=0$: \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\varphi \\{\rm{v = - A}}\omega {\rm{sin}}\varphi \end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi {\rm{ = }}\frac{{{x_0}}}{A}\\\sin \varphi = - \frac{v}{{A\omega }}\end{array} \right. \to \varphi = ?\) Lời giải chi tiết :
Ta có: \({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {2^2} + \frac{{{{\left( {20\sqrt {15} } \right)}^2}}}{{{{\left( {10\sqrt 5 } \right)}^2}}} = 16 \to A = 4cm\) Tại t=0: \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\varphi = 2\\{\rm{v = - A}}\omega {\rm{sin}}\varphi > 0\end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi {\rm{ = }}\frac{2}{4} = \frac{1}{2}\\\sin \varphi < 0\end{array} \right. \to \varphi = - \frac{\pi }{3}\) \( \Rightarrow x = 4c{\rm{os}}\left( {10\sqrt 5 t - \frac{\pi }{3}} \right)cm\)
Câu 6 :
Khi xảy ra hiện tượng cộng hưởng cơ thì vật tiếp tục dao động:
Đáp án : A Lời giải chi tiết :
Khi xảy ra hiện tượng cộng hưởng cơ thì vật tiếp tục dao động với tần số bằng tần số dao động riêng của vật
Câu 7 :
Một chất điểm dao động điều hòa với phương trình \(x = Acos(\omega t + \varphi )\). Biểu thức vận tốc tức thời của chất điểm là:
Đáp án : B Lời giải chi tiết :
$v = x' = - \omega Asin(\omega t + \varphi ) = \omega Acos(\omega t + \varphi + \frac{\pi }{2})$
Câu 8 :
Khi xảy ra hiện tượng cộng hưởng thì:
Đáp án : D Lời giải chi tiết :
Ta có, khi xảy ra hiện tượng cộng hưởng: + Vật dao động với tần số bằng tần số dao động riêng + Biên độ dao động của vật đạt giá trị cực đại => năng lượng dao động của vật đạt giá trị cực đại
Câu 9 :
Một vật dao động điều hòa với chu kỳ T và biên độ là A. Ban đầu vật ở vị trí cân bằng, khoảng thời gian ngắn nhất kể từ khi vật dao động đến thời điểm mà động năng bằng thế năng là:
Đáp án : B Phương pháp giải :
+ Áp dụng biểu thức xác định cơ năng: \({\rm{W}} = {{\rm{W}}_t} + {{\rm{W}}_{\rm{d}}}\) + Sử dụng trục thời gian suy ra từ vòng tròn Lời giải chi tiết :
Vị trí: \({{\text{W}}_t} = {{\text{W}}_d} \to 2{{\text{W}}_t} = {\text{W}} \to x = \pm \dfrac{A}{{\sqrt 2 }}\)  => Khoảng thời gian ngắn nhất kể từ khi vật dao động đến thời điểm mà động năng bằng thế năng là: \(\dfrac{T}{8}\)
Câu 10 :
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương cùng tần số. Biết dao động thứ nhất có biên độ \(A_1= 6 cm\) và trễ pha \(\dfrac{\pi}{2}\) so với dao động tổng hợp. Tại thời điểm dao động thứ hai có li độ bằng biên độ của dao động thứ nhất thì dao động tổng hợp có li độ \(9 cm\). Biên độ dao động tổng hợp bằng:
Đáp án : D Phương pháp giải :
Sử dụng giản đồ Fresnen Lời giải chi tiết :
Dao động tổng hợp: \(x=x_1+x_2\) Tại thời điểm dao động thứ hai có li độ bằng biên độ của dao động thứ nhất thì dao động tổng hợp có li độ \(9 cm\), ta có: \(x_1+6cm=9cm\) => \(x_1= 3cm\) Dựa vào đề bài ta biểu diễn được các véc tơ dao động như hình bên. 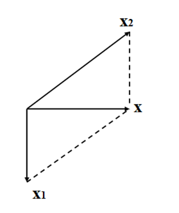 Hai dao động vuông pha nên ta có: \(\dfrac{{x_1^2}}{{A_1^2}} + \dfrac{{x_{}^2}}{{A_{}^2}} = 1 \Leftrightarrow \dfrac{{{3^2}}}{{{6^2}}} + \dfrac{{{9^2}}}{{{A^2}}} = 1 \Rightarrow A = 6\sqrt 3 cm\)
Câu 11 :
Một con lắc lò xo dao động điều hòa gồm lò xo có độ cứng k và vật có khối lượng m. Khi k = k1 thì chu kì dao động của con lắc là T1, khi k = k2 thì chu kì dao động của con lắc là T2. Khi mắc song song k1 với k2 thì chu kì dao động của con lắc là:
Đáp án : B Lời giải chi tiết :
Ta có: \(T = 2\pi \sqrt {\dfrac{m}{k}} \to {T^2} \sim \dfrac{1}{k}\) Song song: k = k1 + k2 Þ cùng treo một vật khối lượng như nhau thì: \(\dfrac{1}{{{T^2}}} = \dfrac{1}{{T_1^2}} + \dfrac{1}{{T_2^2}}\)
Câu 12 :
Một chất điểm dao động điều hòa theo phương trình \(x = 4cos\left( {4\pi t + \dfrac{\pi }{2}} \right)cm\). Quãng đường vật đi được sau \(1s\) là:
Đáp án : A Phương pháp giải :
+ Áp dụng biểu thức tính chu kì: \(T = \dfrac{{2\pi }}{\omega }\) + Vận dụng công thức quãng đường đi được của vật trong 1 chu kì: \(S = 4A\) Lời giải chi tiết :
Ta có: + Chu kì dao động của vật: \(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{4\pi }} = 0,5{\rm{s}}\) +\(\Delta t = 1s = 2T\) Trong 1 chu kì vật đi được quãng đường \(4A\) => Quãng đường vật đi được sau \(\Delta t = 1s = 2T\) là: \(2.4A = 2.4.4 = 32cm\)
Câu 13 :
Khi nói về dao động điều hoà của một vật, phát biểu nào sau đây đúng?
Đáp án : D Lời giải chi tiết :
A – sai vì: Gia tốc luôn hướng về vị trí cân bằng, vận tốc trong 1 chu kì đổi chiều 2 lần B – sai vì: Chuyển động của vật từ VTCB ra biên là chuyển động chậm dần C – sai vì: Gia tốc luôn hướng về VTCB D - đúng
Câu 14 :
Một con lắc đơn dao động với phương trình \(s = 2cos\left( {2\pi t} \right)cm\) (t tính bằng giây). Tần số dao động của con lắc là:
Đáp án : A Phương pháp giải :
Vận dụng biểu thức tính tần số \(f = \dfrac{1}{T} = \dfrac{\omega }{{2\pi }}\) Lời giải chi tiết :
Ta có, phương trình dao động của con lắc đơn: \(s = 2cos\left( {2\pi t} \right)cm\) => Tần số góc dao động của con lắc: \(\omega = 2\pi \left( {rad/s} \right)\) => Tần số dao động của con lắc: \(f = \dfrac{\omega }{{2\pi }} = \dfrac{{2\pi }}{{2\pi }} = 1Hz\)
Câu 15 :
Một vật dao động điều hòa với phương trình \(x = Acos\left( {\omega t + \varphi } \right)\). Tại thời điểm ban đầu \(t = 0\), vật ở vị trí \(x = - A\). Pha ban đầu của dao động là:
Đáp án : B Phương pháp giải :
Thay \(t = 0\) vào phương trình li độ kết hợp với điều kiện đầu bài ta suy ra pha ban đầu \(\varphi \) Lời giải chi tiết :
Ta có, \(t = 0 \to x = Acos\varphi \) Theo đầu bài, ta có: \(\begin{array}{l}x = - A \leftrightarrow Acos\varphi = - A\\ \to cos\varphi = - 1 \to \varphi = \pi \end{array}\)
Câu 16 :
Tại một nơi xác định, chu kì dao động điều hòa của con lắc đơn tỉ lệ nghịch với:
Đáp án : C Phương pháp giải :
Vận dụng biểu thức tính chu kì dao động của con lắc đơn: \(T = 2\pi \sqrt {\frac{l}{g}} \) Lời giải chi tiết :
Ta có chu kì dao động của con lắc đơn: \(T = 2\pi \sqrt {\frac{l}{g}} \) => Chu kì dao động của con lăc đơn tỉ lệ thuận với căn bậc 2 chiều dài con lắc và tỉ lệ nghịch với căn bậc hai gia tốc trọng trường
Câu 17 :
Một con lắc đơn đang dao động điều hòa với biên độ góc bằng \(9,{6^0}\) dưới tác dụng của trọng lực. Ở thời điểm \({t_0}\), vật nhỏ của con lắc có li độ góc và li độ cong lần lượt là \(4,{8^0}\) và \(3,2\pi cm\). Lấy \(g{\rm{ }} = {\rm{ }}10{\rm{ }}m/{s^2}\). Tốc độ của vật ở thời điểm \({t_0}\) bằng:
Đáp án : C Phương pháp giải :
+ Áp dụng mối liên hệ giữa li độ dài và li độ góc: \(s = l\alpha \) + Áp dụng công thức tính vận tốc của con lắc đơn dao động điều hòa: \(v = \sqrt {gl(\alpha _0^2 - {\alpha ^2})} \) Lời giải chi tiết :
Ta có: \(9,{6^0} = \dfrac{{9,6\pi }}{{180}} \approx 0,17rad\) \(4,{8^0} = \dfrac{{4,8\pi }}{{180}} \approx 0,0834rad\) + Theo bài ra ta có: \(s = l\alpha \) Ta suy ra: \(l = \dfrac{s}{\alpha } = \dfrac{{3,2\pi }}{{\dfrac{{4,8\pi }}{{180}}}} = 120cm\) Ta có, vận tốc: \(v = \sqrt {gl\left( {\alpha _0^2 - {\alpha ^2}} \right)} \\ = \sqrt {10.1,2\left( {0,{{17}^2} - 0,{{0834}^2}} \right)} \\\approx 0,513m/s = 51,3cm/s\) Chú ý
Đổi độ sang rad
Câu 18 :
Một con lắc lò xo đang dao động tắt dần, cơ năng ban đầu của nó là \(6J\). Sau bốn chu kì kể từ lúc bắt đầu dao động thì biên độ của nó giảm đi \(24\% \). Phần cơ năng của con lắc chuyển hóa thành nhiệt năng tính trung bình trong mỗi chu kì dao động của nó là:
Đáp án : C Lời giải chi tiết :
+ Sau bốn chu kì dao động, biên độ còn lại của con lắc là: \({A_4} = A - 0,24A = 0,76A\) + Phần năng lượng bị mất đi sau bốn chu kì: \(\begin{array}{l}\Delta {E_4} = E - {E_4} = \frac{{E - {E_4}}}{E}E = \frac{{\frac{1}{2}k{A^2} - \frac{1}{2}kA_4^2}}{{\frac{1}{2}k{A^2}}}E\\ = \frac{{{A^2} - {{(0,76A)}^2}}}{{{A^2}}}.6 = 2,5344J\end{array}\) + Phần cơ năng chuyển hóa thành nhiệt năng trung bình trong mỗi chu kì: \(\Delta E = \frac{{2,5344}}{4} = 0,6336J\)
Câu 19 :
Một vật thực hiện đồng thời hai dao động điều hòa cùng phương cùng tần số có phương trình lần lượt là: \({x_1} = {\rm{ }}{A_1}cos\left( {\omega t + {\varphi _1}} \right)\) và \({x_2} = {\rm{ }}{A_2}cos\left( {\omega t + {\varphi _2}} \right)\). Biên độ dao động A của vật được xác định bởi công thức nào sau đây?
Đáp án : A Lời giải chi tiết :
Biên độ dao động tổng hợp A được xác định bởi biểu thức: \(A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}\cos ({\varphi _2} - {\varphi _1})} \)
Câu 20 :
Dao động tổng hợp của hai dao động điều hòa cùng phương, cùng tần số có phương trình li độ là \(x = 4cos\left( {2\pi t - \dfrac{\pi }{6}} \right)cm\). Biết dao động thứ nhất có phương trình li độ là \({x_1} = 3cos\left( {2\pi t + \dfrac{\pi }{3}} \right)\). Dao động thứ hai có phương trình li độ là:
Đáp án : D Phương pháp giải :
+ Xác định phương trình dao động thành phần: \({x_2} = x - {x_1}\) + Sử dụng công thức lượng giác: \( - cos\alpha = cos\left( {\alpha + \pi } \right)\) + Sử dụng lí thuyết về tổng hợp hai dao động điều hòa cùng tần số Lời giải chi tiết :
Ta có : \(x{\rm{ }} = {\rm{ }}{x_1} + {\rm{ }}{x_2} \to {x_2} = {\rm{ }}x{\rm{ }}-{\rm{ }}{x_1}\) \(x = 4cos\left( {2\pi t - \dfrac{\pi }{6}} \right)cm\) \({x_1} = 3cos\left( {2\pi t + \dfrac{\pi }{3}} \right)\) Ta suy ra: \(\begin{array}{l}{x_2} = x - {x_1} = 4cos\left( {2\pi t - \dfrac{\pi }{6}} \right) - 3cos\left( {2\pi t + \dfrac{\pi }{3}} \right)\\ = 4cos\left( {2\pi t - \dfrac{\pi }{6}} \right) + 3cos\left( {2\pi t + \dfrac{\pi }{3} + \pi } \right)\end{array}\) Biên độ dao động của 2 : \({A_2} = \sqrt {{4^2} + {3^2} + 2.4.3.cos\left( {\pi + \dfrac{\pi }{3} - \left( { - \dfrac{\pi }{6}} \right)} \right)} = 5cm\) Pha ban đầu của dao động 2 : \(\begin{array}{l}\tan {\varphi _2} = \dfrac{{4\sin \left( { - \dfrac{\pi }{6}} \right) + 3\sin \left( {\dfrac{\pi }{3} + \pi } \right)}}{{4cos\left( { - \dfrac{\pi }{6}} \right) + 3cos\left( {\dfrac{\pi }{3} + \pi } \right)}} = - 2,34\\ \to {\varphi _2} = - 66,{8^0} \approx - 1,17\left( {rad} \right)\end{array}\) \( \to {x_2} = 5cos\left( {2\pi t - 1,17} \right)cm\)
Câu 21 :
Phát biểu nào sau đây là đúng?
Đáp án : D Phương pháp giải :
Sử dụng lí thuyết và biểu thức tính cơ năng Lời giải chi tiết :
A – sai vì: Cơ năng của con lắc lò xo dao động điều hòa được bảo toàn B – sai vì: Động năng và thế năng của con lắc lò xo luôn thay đổi C – sai vì: Trong dao động điều hòa của con lắc lò xo, động năng tăng bao nhiêu thì thế năng giảm bấy nhiêu. D - đúng
Câu 22 :
Một vật dao động điều hòa với chu kỳ \(T\) và biên độ \(A\). Khoảng thời gian ngắn nhất vật đi từ vị trí có động năng bằng thế năng đến vị trí có động năng bằng 3 lần thế năng là?
Đáp án : D Phương pháp giải :
+ Áp dụng biểu thức xác định cơ năng: \({\rm{W}} = {{\rm{W}}_t} + {{\rm{W}}_{\rm{d}}}\) + Sử dụng vòng tròn lượng giác và biểu thức: \(\Delta \varphi = \omega \Delta t\) Lời giải chi tiết :
Ta có: + Vị trí có động năng bằng thế năng: \({{\rm{W}}_t} = {{\rm{W}}_{đ}} \to 2{{\rm{W}}_t} = {\rm{W}} \to {x_1} = \pm \dfrac{A}{{\sqrt 2 }}\) + Vị trí có động năng bằng 3 lần thế năng: \({{\rm{W}}_d} = 3{{\rm{W}}_t} \to {{\rm{W}}_t} = \dfrac{{\rm{W}}}{4} \to {x_2} = \pm \dfrac{A}{2}\) Xác định các vị trí trên vòng tròn lượng giác, ta được:
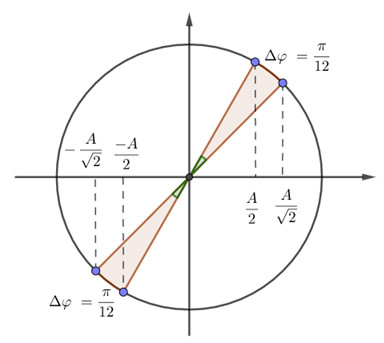
Thời gian ngắn nhất vật đi từ vị trí có động năng bằng thế năng đến vị trí có động năng bằng 3 lần thế năng tương ứng với góc quét: \(\Delta \varphi = \dfrac{\pi }{{12}}\) Mặt khác, \(\begin{array}{l}\Delta \varphi = \omega \Delta t \leftrightarrow \dfrac{\pi }{{12}} = \dfrac{{2\pi }}{T}.\Delta t\\ \to \Delta t = \dfrac{T}{{24}}\end{array}\) Thời gian ngắn nhất vật đi từ vị trí có động năng bằng thế năng đến vị trí có động năng bằng 3 lần thế năng là \(\dfrac{T}{{24}}\)
Câu 23 :
Khi gắn vật có khối lượng \({m_1} = 3kg\) vào một lò xo có khối lượng không đáng kể, nó dao động với chu kì \({T_1} = 1,2s\). Khi gắn một vật khác có khối lượng \({m_2}\) vào lò xo trên nó dao động với chu kì \({T_2} = 0,6s\). Khối lượng \({m_2}\) bằng?
Đáp án : A Phương pháp giải :
Áp dụng biểu thức xác định chu kì dao động của con lắc lò xo: \(T = 2\pi \sqrt {\dfrac{m}{k}} \) Lời giải chi tiết :
Chu kì dao động của vật: \(T = 2\pi \sqrt {\dfrac{m}{k}} \) \( \to \dfrac{{{T_1}}}{{{T_2}}} = \sqrt {\dfrac{{{m_1}}}{{{m_2}}}} \to {m_2} = \dfrac{{{m_1}T_2^2}}{{T_1^2}} = \dfrac{{3.0,{6^2}}}{{1,{2^2}}} = 0,75kg\)
Câu 24 :
Một con lắc lò xo có độ cứng \(k = 160N/m\), đầu trên cố định còn đầu dưới gắn vật nặng \(m = 1,2kg\). Cho vật \(m\) dao động điều hòa theo phương thẳng đứng thì thấy thời gian lò xo nén trong một chu kì là \(0,14s\). Cho \(g = {\pi ^2} = 10m/{s^2}\). Biên độ dao động của vật là:
Đáp án : A Phương pháp giải :
+ Sử dụng công thức tính độ dãn của lò xo ở VTCB: \(\Delta l = \dfrac{{mg}}{k}\) + Sử dụng công thức tính chu kỳ dao động của con lắc: \(T = 2\pi \sqrt {\dfrac{m}{k}} \) + Vận dụng tỉ số thời gian nén trên chu kì => tỉ lệ => Biên độ Lời giải chi tiết :
Ta có: + Độ dãn của lò xo ở VTCB: \(\Delta l = \dfrac{{mg}}{k} = \dfrac{{1,2.10}}{{160}} = 0,075m = 7,5cm\) Chu kỳ dao động của con lắc: \(T = 2\pi \sqrt {\dfrac{m}{k}} = 2\pi \sqrt {\dfrac{{1,2}}{{160}}} \approx 0,55{\rm{s}}\) \(\dfrac{{{t_n}}}{T} = \dfrac{{0,14}}{{0,55}} \approx 0,25 \to {t_n} = 0,25T = \dfrac{T}{4}\)
Ta có: \(\Delta \varphi = \omega \Delta t = \dfrac{{2\pi }}{T}.\dfrac{T}{4} = \dfrac{\pi }{2}\) \(\begin{array}{l} \to \Delta l = Acos\dfrac{{\Delta \varphi }}{2} = Acos\dfrac{\pi }{4} = \dfrac{A}{{\sqrt 2 }}\\ \to A = \sqrt 2 \Delta l = 7,5\sqrt 2 cm\end{array}\)
Câu 25 :
Hai con lắc lò xo giống nhau được treo vào hai điểm ở cùng độ cao, cách nhau \(4cm\). Kích thích cho hai con lắc dao động điều hòa theo phương thẳng đứng thì đồ thị biểu diễn sự phụ thuộc của li độ \(x\) vào thời gian \(t\) của hai vật như hình vẽ. Kể từ thời điểm \(t = 0\), hai vật cách nhau \(4\sqrt 3 cm\) lần thứ 2019 là 
Đáp án : B Phương pháp giải :
Liên hệ giữa chu kỳ dao động và tần số góc \(\omega = \dfrac{{2\pi }}{T}\) Tổng hợp hai dao động điều hòa cùng phương cùng tần số cũng là một dao động điều hào cùng tần số Khoảng cách giữa hai vật \(d=\sqrt{a^2+{\Delta x}^2}\) Lời giải chi tiết :
Từ hình vẽ ta được chu kỳ của hai vật bằng nhau \(T = 1,44s\) Tần số góc \(\omega = \dfrac{{2\pi }}{T} = \dfrac{{25\pi }}{{18}}(rad/s)\) + Con lắc (1) có biên độ A1 = 4cm, thời điểm ban đầu có x = 2cm theo chiều âm nên pha ban đầu φ1 = π/3 + Con lắc (2) ở thời điểm t = 0,48s = T/3 đi qua vị trí cân bằng theo chiều âm, thời điểm ban đầu có x = 6cm theo chiều dương. Vậy pha ban đầu φ2 = -π/6 và A2 =\(4\sqrt 3 cm\) Phương trình dao động của hai con lắc là \({x_1} = 4\cos (\dfrac{{10\pi t}}{9} + \dfrac{\pi }{3})cm;{x_2} = 4\sqrt 3 {\rm{cos(}}\dfrac{{10\pi t}}{9} - \dfrac{\pi }{6})\) Ta có: x = x1 – x2 = \(4\cos (\dfrac{{10\pi t}}{9} + \dfrac{\pi }{3}) + 4\sqrt 3 {\rm{cos(}}\dfrac{{10\pi t}}{9} - \dfrac{\pi }{6} + \pi ) = 8\cos (\dfrac{{10\pi t}}{9} + \dfrac{{2\pi }}{3})cm\) Khoảng cách giữa hai vật là \(4\sqrt 3 cm\) ứng với \(d=\sqrt{a^2+{\Delta x}^2}=4\sqrt 3=\sqrt{4^2+{x}^2}\) \(\to x = ± 4\sqrt 2 cm\) Trong 1 chu kỳ có 4 lần vật đi qua vị trí \(x = ±4\sqrt 2 cm\) => Sau 504T có 2016 lần vật đi qua vị trí \(x = ±4\sqrt 2 cm\) và trở về vị trí ban đầu. Vậy thời điểm vật đi qua vị trí có \(x = ±4\sqrt 2 cm\) lần thứ 2019 là : \(t = 504T + \dfrac{T}{6} + \dfrac{3T}{{8}}=726,54s\) |




















Danh sách bình luận