Đề kiểm tra giữa học kì 2 - Đề số 4Đề bài
Câu 1 :
Ánh sáng trên bề mặt rộng 7,2 mm của vùng giao thoa người ta đếm được 9 vân sáng (hai rìa là hai vân sáng). Tại vị trí cách vân trung tâm 14,4 mm ℓà vân:
Câu 2 :
Tìm phát biểu sai. Dao động điện từ trong mạch dao động LC bị tắt dần là do:
Câu 3 :
Chùm tia sáng ló ra khỏi lăng kính của một máy quang phổ, trước khi đi qua thấu kính buồng tối là
Câu 4 :
Chiếu ánh sáng trắng do một nguồn nóng sáng phát ra vào khe hẹp F của một máy quang phổ lăng kính thì trên tấm kính ảnh (hoặc tấm kính mờ) của buồng ảnh sẽ thu được:
Câu 5 :
Trong thí nghiệm I- âng về giao thoa ánh sáng đơn sắc, người ta thấy khoảng vân tăng thêm 0,3mm khi dời màn để khoảng cách giữa màn và hai khe thay đổi một đoạn 0,5m. Biết hai khe cách nhau là a = 1mm. Bước sóng của ánh sáng đã sử dụng là?
Câu 6 :
Trong thí nghiệm I-âng về giao thoa ánh sáng, khoảng cách giữa hai khe là a = 1mm, từ hai khe đến màn hứng là D = 2m, nguồn sáng gồm hai bức xạ đơn sắc λ1 = 0,6 µm và λ2 = 0,5 µm, nếu hai vân sáng của hai bức xạ trùng nhau ta chỉ tính là một vân sáng. Khoảng cách nhỏ nhất giữa hai vân sáng trùng nhau quan sát được trên màn là:
Câu 7 :
Trong sơ đồ khối của một máy phát thanh dùng vô tuyến không có bộ phận nào dưới đây?
Câu 8 :
Trong thí nghiệm Young về giao thoa ánh sáng, nguồn sáng phát đồng thời hai bức xạ đơn sắc có bước sóng λ1 = 704 nm và λ2 = 440 nm. Trên màn quan sát, giữa hai vân sáng gần nhau nhất và cùng màu với vân trung tâm, số vân sáng khác màu với vân trung tâm là
Câu 9 :
Dụng cụ nào dưới đây có cả máy phát và máy thu sóng vô tuyến?
Câu 10 :
Trong công nghiệp cơ khí, dựa vào tính chất nào sau đây của tia tử ngoại mà người ta sử dụng để tìm vết nứt trên bề mặt các vật kim loại:
Câu 11 :
Một nguồn sáng đơn sắc có \(\lambda \) = 0,6\(\mu \)m chiếu vào mặt phẳng chứa hai khe hẹp, hai khe cách nhau 1mm. Màn ảnh cách màn chứa hai khe là 1m. Khoảng cách gần nhất giữa hai vân tối là:
Câu 12 :
Nhóm tia nào sau đây có cùng bản chất sóng điện từ?
Câu 13 :
Nhận xét nào sau đây liên quan đến năng lượng điện từ của mạch dao động là sai?
Câu 14 :
Khi mắc cuộn cảm có độ tự cảm L1 với tụ điện có điện dung C thì tần số dao động của mạch là f1 = 3 kHz, khi mắc cuộn cảm có độ tự cảm L2 với tụ điện có điện dung C thì tần số dao động của mạch là f2= 4 kHz. Tần số dao động của mạch khi mắc L1 nối tiếp với L2 và tần số dao động của mạch khi mắc L1 song song L2 là:
Câu 15 :
Phát biểu nào sau đây là không đúng?
Câu 16 :
Một bức xạ truyền trong không khí với chu kỳ $8,{25.10^{ - 16}}s$. Bức xạ này thuộc vùng nào của thang sóng điện từ?
Câu 17 :
Trong thí nghiệm Y-âng, khoảng cách giữa hai khe là $1mm$, khoảng cách từ hai khe tới màn là $2m$, ánh sáng có bước sóng ${\lambda} = {\rm{ }}0,66\mu m$. Nếu độ rộng của vùng giao thoa trên màn là: $13,2mm$ thì số vân sáng và vân tối trên màn là:
Câu 18 :
Trong thí nghiệm Y-âng về giao thoa ánh sáng trắng, trên màn quan sát thu được hình ảnh giao thoa gồm:
Câu 19 :
Bước sóng của một ánh sáng đơn sắc trong không khí là $600{\rm{ }}nm$. Bước sóng của nó trong nước có giá trị là bao nhiêu? Biết chiết suất của nước \(n = \dfrac{4}{3}\)
Câu 20 :
Phát biểu nào sau đây không đúng khi nói về tính chất của sóng điện từ?
Câu 21 :
Xone FM có tần số \(102,7MHz\), sóng vô tuyến do đài này phát ra thuộc loại:
Câu 22 :
Một mạch dao động LC gồm tụ điện có điện dung $C{\rm{ }} = {\rm{ }}8nF$ và một cuộn dây thuần cảm có độ tự cảm $L{\rm{ }} = {\rm{ }}2mH$. Biết hiệu điện thế cực đại trên tụ là $6V$. Khi cường độ dòng điện trong mạch bằng $6mA$, thì hiệu điện thế giữa hai đầu cuộn cảm bằng:
Câu 23 :
Thực hiện thí nghiệm giao thoa khe Iâng với nguồn bức xạ đơn sắc. Điểm M trên màn quan sát có vân sáng bậc 4. Từ vị trí ban đầu của màn, ta dịch chuyển màn ra xa hai khe một đoạn 30 cm thì tại M quan sát thấy vân tối thứ 3. Từ vị trí ban đầu của màn, ta dịch chuyển màn lại gần hai khe một đoạn 30 cm thì tại M quan sát thấy:
Câu 24 :
Chiếu xiên từ không khí vào nước một chùm sáng song song rất hẹp (coi như một tia sáng) gồm ba thành phần đơn sắc: cam, lục và chàm. Gọi \({r_{cam}},{r_{luc}},{r_{cham}}\) lần lượt là góc khúc xạ ứng với tia màu cam, tia màu lục và tia màu chàm. Hệ thức đúng là:
Câu 25 :
Trong một thí nghiệm Y-âng về giao thoa ánh sáng, khoảng cách giữa hai khe là 0,8 mm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là 1,6 m. Nguồn sáng phát ánh sáng trắng có bước sóng trong khoảng từ 380 nm đến 760 nm. M là một điểm trên màn, cách vân sáng trung tâm 1 cm. Trong các bước sóng của các bức xạ cho vân sáng tại M, bước sóng ngắn nhất là
Câu 26 :
Trong thí nghiệm Y-âng về giao thoa ánh sáng, khoảng cách giữa hai khe là 1mm, khoảng cách từ hai khe đến màn là 1,2m. Nguồn S phát áng sáng trắng có bước sóng trong khoảng \(0,4\mu m \le \lambda \le 0,76\mu m\). Tần số lớn nhất của bức xạ đơn sắc cho vân sáng tại điểm M trên màn cách vân trung tâm một đoạn 2,1mm là
Câu 27 :
Theo mẫu nguyên tử Bo, mức năng lượng của trạng thái dừng thứ n của nguyên tử Hidro được xác định theo công thức \({E_n} = - \dfrac{{13,6}}{{{n^2}}}\left( {eV} \right);\left( {n = 1,2,3...} \right)\) Gọi R1 là bán kính quỹ đạo của e khi nguyên tử Hidro ở tạng thái dừng L. Khi nguyên tử ở trạng thái dừng ứng với bán kính bằng 9R1 thì tỷ số bước sóng lớn nhất và bước sóng nhỏ nhất của photon mà nguyên tử Hidro có thể phát xạ là:
Câu 28 :
Một mạch dao động ở máy vào của một máy thu thanh gồm cuộn thuần cảm có độ tự cảm 3 µH và tụ điện có điện dung biến thiên trong khoảng từ 10 pF đến 500pF. Biết rằng, muốn thu được sóng điện từ thì tần số riêng của mạch dao động phải bằng tần số của sóng điện từ cần thu (để có cộng hưởng). Trong không khí, tốc độ truyền sóng điện từ là 3.108 m/s, máy thu này có thể thu được sóng điện từ có bước sóng trong khoảng
Câu 29 :
Một mạch dao động lí tưởng gồm cuộn cảm thuần có độ tự cảm L không đổi và tụ điện có điện dung C thay đổi được. Điều chỉnh điện dung của tụ điện đến giá trị C1 thì tần số dao động riêng của mạch là f1. Để tần số dao động riêng của mạch là \(\sqrt 5 {f_1}\) thì phải điều chỉnh điện dung của tụ điện đến giá trị
Câu 30 :
Trong mạch dao động lí tưởng đang có dao động điện từ tự do với chu kỳ T. Biết tụ điện có điện dung \(2nF\) và cuộn cảm có độ tự cảm \(8mH\). Tại thời điểm t1, cường độ dòng điện trong mạch có độ lớn \(5 mA\). Tại thời điểm t2 = t1 + 2π.10-6(s) điện áp giữa hai bản tụ có độ lớn
Câu 31 :
Để truyền thông tin liên lạc bằng sóng vô tuyến, người ta sử dụng phương pháp biến điệu biên độ, trong đó sóng cao tần có tần số \(800 kHz\) và sóng âm tần có tần số \(1 kHz\). Tần số của sóng sau khi biến điệu là
Câu 32 :
Trong chân không, ánh sáng nhìn thấy được có bước sóng trong khoảng từ
Câu 33 :
Gọi nđ, nt và nv lần lượt là chiết suất của một môi trường trong suốt đối với các ánh sáng đơn sắc đỏ, tím và vàng. Sắp xếp nào sau đây là đúng?
Câu 34 :
Trong thí nghiệm Y‒âng về giao thoa ánh sáng, người ta sử dụng nguồn phát ánh sáng trắng có bước sóng từ \(400 nm\) đến \(760 nm\). Trên màn quan sát, \(M\) là vị trí mà tại đó có đúng \(6\) bức xạ cho vân sáng, trong đó có vân sáng của hai bức xạ có bước sóng là \(680 nm\) và \(544 nm\). Tại \(M\) cũng là vị trí vân tối của một số bức xạ khác trong đó bức xạ có bước sóng ngắn nhất là \({\lambda _{min}}\). Giá trị \({\lambda _{min}}\) gần nhất với giá trị nào sau đây?
Câu 35 :
Một mạch dao động có tụ điện với điện dung \(C = 6pF\), cuộn cảm có hệ số tự cảm \(L = 2,4mH\) và điện trở hoạt động \(R = 5\Omega \). Để duy trì dao động của mạch như ban dầu thì cần nguồn cung cấp cho mạch có công suất \(45\mu W\). Hiệu điện thế cực đại trên tụ là?
Câu 36 :
Một mạch dao động LC đang thu được sóng trung. Để mạch có thể thu được sóng dài thì phải
Câu 37 :
Một máy thu thanh đang thu được sóng ngắn. Để chuyển sang thu sóng cực ngắn, có thể thực hiện giải pháp nào sau đây trong mạch dao động anten
Câu 38 :
Điện dung của tụ điện phải thay đổi trong khoảng nào để mạch có thể thu được sóng vô tuyến có bước sóng nằm trong khoảng từ \({\lambda _1}\) đến \({\lambda _2}\) (\({\lambda _1} < {\lambda _2}\)). Chọn kết quả đúng:
Câu 39 :
Trong mạch dao động LC có điện trở thuần bằng không thì năng lượng
Câu 40 :
Trong một thí nghiệm Y – âng về giao thoa ánh sáng, có a = 1mm, D = 2m. Nếu chiếu đồng thời hai bức xạ đơn sắc có bước sóng λ1 = 0,6μm; λ2 = 0,5μm thì trên màn quan sát có những vị trí tại đó có vân sáng của hai bức xạ trùng nhau gọi là vân trùng. Khoảng cách ngắn nhất giữa hai vân trùng bằng
Lời giải và đáp án
Câu 1 :
Ánh sáng trên bề mặt rộng 7,2 mm của vùng giao thoa người ta đếm được 9 vân sáng (hai rìa là hai vân sáng). Tại vị trí cách vân trung tâm 14,4 mm ℓà vân:
Đáp án : D Phương pháp giải :
+ Áp dụng biểu thức tính khoảng cách giữa N vân sáng liên tiếp là (N-1)i + Áp dụng biểu thức xác định tính chất, vị trí vân sáng - tối Lời giải chi tiết :
Ta có, trên màn có 9 vân sáng => Khoảng cách giữa 9 vân sáng là 8i = 7,2mm => i = 0,9mm Tại vị trí cách trung tâm 14,4mm = 16i => Vân sáng thứ 16
Câu 2 :
Tìm phát biểu sai. Dao động điện từ trong mạch dao động LC bị tắt dần là do:
Đáp án : D Lời giải chi tiết :
A, B, C - đúng Mạch dao động điện từ tự do (mạch dao động LC lí tưởng) có năng lượng điện trường tập trung trong tụ điện và năng lượng từ trường tập trung trong cuộn cảm. Hai năng lượng này luôn chuyển hóa lẫn nhau => Sự chuyển hóa năng lượng điện trường sang từ trường và ngược lại không là nguyên nhân gây tắt dần dao động => D - sai
Câu 3 :
Chùm tia sáng ló ra khỏi lăng kính của một máy quang phổ, trước khi đi qua thấu kính buồng tối là
Đáp án : A Phương pháp giải :
+ Sử dụng lí thuyết về cấu tạo của máy quang phổ lăng kính (Xem lí thuyết phần 1) + Vận dụng hiện tượng tán sắc ánh sáng Lời giải chi tiết :
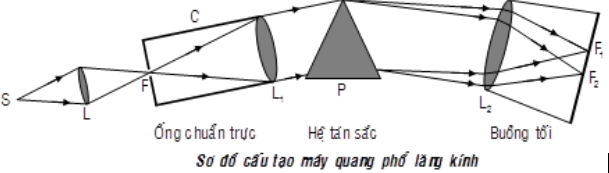
Câu 4 :
Chiếu ánh sáng trắng do một nguồn nóng sáng phát ra vào khe hẹp F của một máy quang phổ lăng kính thì trên tấm kính ảnh (hoặc tấm kính mờ) của buồng ảnh sẽ thu được:
Đáp án : B Phương pháp giải :
+ Sử dụng lí thuyết về cấu tạo của máy quang phổ lăng kính (Xem lí thuyết phần 1) + Vận dụng hiện tượng tán sắc ánh sáng Lời giải chi tiết :
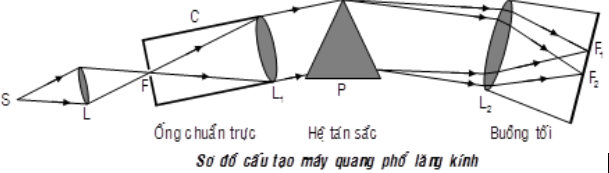
Câu 5 :
Trong thí nghiệm I- âng về giao thoa ánh sáng đơn sắc, người ta thấy khoảng vân tăng thêm 0,3mm khi dời màn để khoảng cách giữa màn và hai khe thay đổi một đoạn 0,5m. Biết hai khe cách nhau là a = 1mm. Bước sóng của ánh sáng đã sử dụng là?
Đáp án : C Phương pháp giải :
Vận dụng biểu thức tính khoảng vân: \(i = \frac{{\lambda D}}{a}\) Lời giải chi tiết :
Gọi i và i’ là khoảng vân ban đầu và sau khi dời màn D, D’ là khoảng cách giữa hai khe và màn lúc ban đầu và sau khi dời màn Ta có: + Ban đầu: \(i = \frac{{\lambda D}}{a}\) + Khi dời màn : \(i' = \frac{{\lambda D'}}{a}\) Mặt khác, theo đầu bài: Khoảng vân tăng thêm 0,3mm khi khoảng cách giữa màn và hai khe thay đổi 0,5m => \(D' > D \to D' = D + 0,5\) \(\begin{array}{l}i' - i = 0,3mm = \Delta i \leftrightarrow \frac{{\lambda D'}}{a} - \frac{{\lambda D}}{a} = \Delta i\\ \leftrightarrow \frac{\lambda }{a}(D' - D) = \Delta i \to \lambda = \frac{{\Delta i.a}}{{D' - D}} = \frac{{0,{{3.10}^{ - 3}}{{.10}^{ - 3}}}}{{0,5}} = 0,{6.10^{ - 6}}m\end{array}\)
Câu 6 :
Trong thí nghiệm I-âng về giao thoa ánh sáng, khoảng cách giữa hai khe là a = 1mm, từ hai khe đến màn hứng là D = 2m, nguồn sáng gồm hai bức xạ đơn sắc λ1 = 0,6 µm và λ2 = 0,5 µm, nếu hai vân sáng của hai bức xạ trùng nhau ta chỉ tính là một vân sáng. Khoảng cách nhỏ nhất giữa hai vân sáng trùng nhau quan sát được trên màn là:
Đáp án : B Phương pháp giải :
Sử dụng lí thuyết về hai vân sáng trùng nhau trong giao thoa ánh sáng Hai vân trùng nhau : x1 = x2 Vị trí vân sáng: xs = kλD/a Lời giải chi tiết :
Ta có: i1 = 1,2mm; i2 = 1mm Khoảng cách nhỏ nhất giữa hai vân sáng = khoảng vân trùng \(\frac{{{k_1}}}{{{k_2}}} = \frac{{{\lambda _2}}}{{{\lambda _1}}} = \frac{5}{6} \Rightarrow {i_T} = 5{i_1} = \frac{{5.{\lambda _1}D}}{a} = 6mm\)
Câu 7 :
Trong sơ đồ khối của một máy phát thanh dùng vô tuyến không có bộ phận nào dưới đây?
Đáp án : A Phương pháp giải :
Xem lí thuyết phần 2 Lời giải chi tiết :
Trong sơ đồ khối của một máy phát thanh dùng vô tuyến không có bộ phận mạch tách sóng
Câu 8 :
Trong thí nghiệm Young về giao thoa ánh sáng, nguồn sáng phát đồng thời hai bức xạ đơn sắc có bước sóng λ1 = 704 nm và λ2 = 440 nm. Trên màn quan sát, giữa hai vân sáng gần nhau nhất và cùng màu với vân trung tâm, số vân sáng khác màu với vân trung tâm là
Đáp án : C Phương pháp giải :
Sử dụng lí thuyết về giao thoa Y – âng với nguồn sáng phát đồng thời hai bức xạ đơn sắc Hai bức xạ trùng nhau: x1 = x2 Vị trí vân sáng: xs = kλD/a Lời giải chi tiết :
Vị trí vân trùng của hai bức xạ: \(\frac{{{k_1}{\lambda _1}D}}{a} = \frac{{{k_2}{\lambda _2}D}}{a} \Leftrightarrow {k_1}{\lambda _1} = {k_2}{\lambda _2} \Rightarrow \frac{{{k_1}}}{{{k_2}}} = \frac{{{\lambda _2}}}{{{\lambda _1}}} = \frac{5}{8} \Rightarrow \left\{ \begin{array}{l}{k_1} = 5n\\{k_2} = 8n\end{array} \right.\) Vân sáng bậc 5n của λ1 trùng với vân sáng bậc 8n của λ2 Xét hai vân sáng gần nhau nhất và cùng màu với vân trung tâm (n = 0 và n = 1) có: 4 vân sáng của λ1 và 7 vân sáng của λ2 Số vân sáng khác màu với vân trung tâm là 4 + 7 = 11.
Câu 9 :
Dụng cụ nào dưới đây có cả máy phát và máy thu sóng vô tuyến?
Đáp án : D Phương pháp giải :
Vận dụng kiến thức thực tế và lí thuyết về thu - phát sóng điện từ Lời giải chi tiết :
Điện thoại di động là dụng cụ có cả máy phát và máy thu sóng vô tuyến
Câu 10 :
Trong công nghiệp cơ khí, dựa vào tính chất nào sau đây của tia tử ngoại mà người ta sử dụng để tìm vết nứt trên bề mặt các vật kim loại:
Đáp án : B Phương pháp giải :
Sử dụng lí thuyết về tia tử ngoại Lời giải chi tiết :
Trong công nghiệp cơ khí, dựa vào tính chất kích thích phát quang nhiều chất của tia tử ngoại mà người ta sử dụng để tìm vết nứt trên bề mặt các vật kim loại.
Câu 11 :
Một nguồn sáng đơn sắc có \(\lambda \) = 0,6\(\mu \)m chiếu vào mặt phẳng chứa hai khe hẹp, hai khe cách nhau 1mm. Màn ảnh cách màn chứa hai khe là 1m. Khoảng cách gần nhất giữa hai vân tối là:
Đáp án : C Phương pháp giải :
Khoảng vân i = λD/a là khoảng cách giữa hai vân sáng liên tiếp hoặc hai vân tối liên tiếp Lời giải chi tiết :
Khoảng cách giữa hai vân tối chính là khoảng vân \(i = \frac{{\lambda D}}{a} = 0,6mm\)
Câu 12 :
Nhóm tia nào sau đây có cùng bản chất sóng điện từ?
Đáp án : C Phương pháp giải :
Sử dụng lí thuyết về các loại tia Lời giải chi tiết :
Ta có: tia tử ngoại, tia hồng ngoại, tia gamma, tia X có bản chất là sóng điện từ
Câu 13 :
Nhận xét nào sau đây liên quan đến năng lượng điện từ của mạch dao động là sai?
Đáp án : C Phương pháp giải :
Xem lí thuyết phần 1 Lời giải chi tiết :
C - sai vì Năng lượng điện trường và năng lượng từ trường biến đổi tuần hoàn theo tần số f’ = 2f và chu kì T’ = T/2
Câu 14 :
Khi mắc cuộn cảm có độ tự cảm L1 với tụ điện có điện dung C thì tần số dao động của mạch là f1 = 3 kHz, khi mắc cuộn cảm có độ tự cảm L2 với tụ điện có điện dung C thì tần số dao động của mạch là f2= 4 kHz. Tần số dao động của mạch khi mắc L1 nối tiếp với L2 và tần số dao động của mạch khi mắc L1 song song L2 là:
Đáp án : A Phương pháp giải :
+ Áp dụng biểu thức xác định tần số dao động của mạch khi ghép nối tiếp cuộn cảm có độ tự cảm L1 và L2: $\frac{1}{{f_{nt}^2}} = \frac{1}{{f_1^2}} + \frac{1}{{f_2^2}}$ + Áp dụng biểu thức xác định tần số dao động của mạch khi ghép song song cuộn cảm có độ tự cảm L1 và L2: $f_{//}^2 = f_1^2 + f_2^2$ Lời giải chi tiết :
Ta có: - Khi mắc cuộn cảm có độ tự cảm L1 thì tần số dao động của mạch là f1 - Khi mắc cuộn cảm có độ tự cảm L2 thì tần số dao động của mạch là f2 - Khi mắc nối tiếp L1 và L2 thì tần số dao động của mạch là: $\frac{1}{{f_{nt}^2}} = \frac{1}{{f_1^2}} + \frac{1}{{f_2^2}} = \frac{{f_1^2 + f_2^2}}{{f_1^2f_2^2}} \to {f_{nt}} = \frac{{{f_1}{f_2}}}{{\sqrt {f_1^2 + f_2^2} }} = \frac{{{{3.10}^3}{{.4.10}^3}}}{{\sqrt {{{({{3.10}^3})}^2} + {{({{4.10}^3})}^2}} }} = 2,{4.10^3}H{\text{z}} = 2,4kH{\text{z}}$ - Khi mắc song song L1 và L2 thì tần số dao động của mạch là: $f_{//}^2 = f_1^2 + f_2^2 \to {f_{//}} = \sqrt {f_1^2 + f_2^2} = \sqrt {{{({{3.10}^3})}^2} + {{\left( {{{4.10}^3}} \right)}^2}} = {5.10^3}H{\text{z}} = 5kH{\text{z}}$
Câu 15 :
Phát biểu nào sau đây là không đúng?
Đáp án : B Lời giải chi tiết :
A, C, D – đúng B – sai vì: Tia hồng ngoại có bước sóng lớn hơn bước sóng của tia tử ngoại
Câu 16 :
Một bức xạ truyền trong không khí với chu kỳ $8,{25.10^{ - 16}}s$. Bức xạ này thuộc vùng nào của thang sóng điện từ?
Đáp án : B Phương pháp giải :
+ Vận dụng biểu thức: \(\lambda = cT\) + Sử dụng thang sóng điện từ:
+ Tia tử ngoại: bức xạ điện từ không nhìn thấy, có bước sóng ngắn hơn bước sóng của ánh sáng tím Lời giải chi tiết :
Bức xạ có bước sóng: $\lambda = cT = {3.10^8}.8,{25.10^{ - 16}} = 2,{475.10^{ - 7}}m = 0,2475\mu m$ => Bức xạ này thuộc vùng tử ngoại
Câu 17 :
Trong thí nghiệm Y-âng, khoảng cách giữa hai khe là $1mm$, khoảng cách từ hai khe tới màn là $2m$, ánh sáng có bước sóng ${\lambda} = {\rm{ }}0,66\mu m$. Nếu độ rộng của vùng giao thoa trên màn là: $13,2mm$ thì số vân sáng và vân tối trên màn là:
Đáp án : A Phương pháp giải :
+ Sử dụng biểu thức tính khoảng vân: \(i = \dfrac{{\lambda D}}{a}\) + Sử dụng công thức xác định số vân sáng, vân tối trên bề rộng miền giao thoa L: ${N_s} = 2\left[ {\dfrac{L}{{2i}}} \right] + 1;{N_t} = 2\left[ {\dfrac{L}{{2i}} + \dfrac{1}{2}} \right]$ Trong đó [ ] là lấy phần nguyên Lời giải chi tiết :
Khoảng vân: $i = \dfrac{{\lambda D}}{a} = \dfrac{{0,66.10^{-6}.2}}{10^{-3}} = 1,32.10^{-3}m=1,32mm$ Độ rộng vùng giao thoa: $L{\rm{ }} = {\rm{ }}13,2{\rm{ }}mm$ Số vân sáng và vân tối trên bề rộng miền giao thoa: $\left\{ \begin{array}{l}{N_s} = 2\left[ {\dfrac{{13,2}}{{2.1,32}}} \right] + 1 = 11\\{N_s} = 2\left[ {\dfrac{{13,2}}{{2.1,32}} + \dfrac{1}{2}} \right] = 10\end{array} \right.$
Câu 18 :
Trong thí nghiệm Y-âng về giao thoa ánh sáng trắng, trên màn quan sát thu được hình ảnh giao thoa gồm:
Đáp án : A Phương pháp giải :
Giao thoa Y–âng với nguồn sáng trắng Ánh sáng trắng là tập hợp của vô số ánh sáng đơn sắc có màu biến thiên liên tục từ đỏ đến tím Lời giải chi tiết :
Trong thí nghiệm giao thoa ánh sáng trắng của I – âng, trên màn quan sát thu được hình ảnh giao thoa gồm chính giữa là vạch sáng trắng, hai bên có những dải màu
Câu 19 :
Bước sóng của một ánh sáng đơn sắc trong không khí là $600{\rm{ }}nm$. Bước sóng của nó trong nước có giá trị là bao nhiêu? Biết chiết suất của nước \(n = \dfrac{4}{3}\)
Đáp án : D Phương pháp giải :
Sử dụng biểu thức tính bước sóng trong môi trường chiết suất n: ${\lambda _n} = \dfrac{\lambda }{n}$ Lời giải chi tiết :
Bước sóng của một ánh sáng đơn sắc trong nước: ${\lambda _n} = \dfrac{{600}}{{\dfrac{4}{3}}} = 450nm$
Câu 20 :
Phát biểu nào sau đây không đúng khi nói về tính chất của sóng điện từ?
Đáp án : D Lời giải chi tiết :
A, B, C – đúng D – sai vì sóng điện từ bị phản xạ ở tầng điện li của Trái Đất
Câu 21 :
Xone FM có tần số \(102,7MHz\), sóng vô tuyến do đài này phát ra thuộc loại:
Đáp án : D Phương pháp giải :
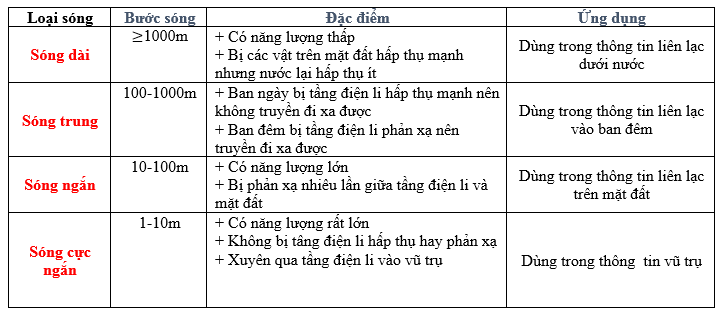
+ Sử dụng biểu thức tính bước sóng: \(\lambda = \dfrac{c}{f}\) + Vận dụng bảng bước sóng vô tuyến:
Lời giải chi tiết :
Ta có: Bước sóng của sóng sóng $\lambda = \dfrac{c}{f} = \dfrac{{{{3.10}^8}}}{{102,{{7.10}^6}}} = 2,92m$ thuộc dải sóng cực ngắn => Sóng do đài này phát ra thuộc sóng cực ngắn
Câu 22 :
Một mạch dao động LC gồm tụ điện có điện dung $C{\rm{ }} = {\rm{ }}8nF$ và một cuộn dây thuần cảm có độ tự cảm $L{\rm{ }} = {\rm{ }}2mH$. Biết hiệu điện thế cực đại trên tụ là $6V$. Khi cường độ dòng điện trong mạch bằng $6mA$, thì hiệu điện thế giữa hai đầu cuộn cảm bằng:
Đáp án : D Phương pháp giải :
Sử dụng công thức tính năng lượng mạch dao động: ${\rm{W}} = {{\rm{W}}_t} + {{\rm{W}}_d} = \dfrac{1}{2}L{i^2} + \dfrac{1}{2}C{u^2} = \dfrac{1}{2}CU_0^2$ Lời giải chi tiết :
Áp dụng công thức tính năng lượng mạch dao động ta có: \(\dfrac{1}{2}C{u^2} + \dfrac{1}{2}L{i^2} = \dfrac{1}{2}CU_0^2\) \( \Leftrightarrow \dfrac{1}{2}{.8.10^{ - 9}}.{u^2} + \dfrac{1}{2}{.2.10^{ - 3}}.{({6.10^{ - 3}})^2} = \dfrac{1}{2}{.8.10^{ - 9}}{.6^2}\) \( = > u = 3\sqrt 3 V\)
Câu 23 :
Thực hiện thí nghiệm giao thoa khe Iâng với nguồn bức xạ đơn sắc. Điểm M trên màn quan sát có vân sáng bậc 4. Từ vị trí ban đầu của màn, ta dịch chuyển màn ra xa hai khe một đoạn 30 cm thì tại M quan sát thấy vân tối thứ 3. Từ vị trí ban đầu của màn, ta dịch chuyển màn lại gần hai khe một đoạn 30 cm thì tại M quan sát thấy:
Đáp án : B Phương pháp giải :
Áp dụng lí thuyết về giao thoa sóng ánh sáng, công thức tính khoảng vân \(i = \dfrac{{\lambda D}}{a}\) Lời giải chi tiết :
+ Khi chưa dịch màn M: \({x_M} = 4i \Rightarrow i = \dfrac{{{x_M}}}{4} = \dfrac{{\lambda D}}{a}\) (1) + Khi dịch màn M ra xa một đoạn 30 cm: \({x_M} = 2,5i' \to i' = \dfrac{{{x_M}}}{{2,5}} = \dfrac{{\lambda (D + 30)}}{a}\) (2) Lấy \(\dfrac{{\left( 2 \right)}}{{\left( 1 \right)}}\), ta được: \(\dfrac{{i'}}{i} = \dfrac{{D + 30}}{D} = \dfrac{{\dfrac{{{x_M}}}{{2,5}}}}{{\dfrac{{{x_M}}}{4}}} = \dfrac{8}{5} \to D = 50(cm)\) + Khi dịch màn M lại gần một đoạn 30 cm: \({x_M} = ki'' \Rightarrow i'' = \dfrac{{{x_M}}}{k} = \dfrac{{\lambda (D - 30)}}{a}\) (3) Lấy \(\dfrac{{\left( 3 \right)}}{{\left( 1 \right)}}\) , ta được: \(\dfrac{{i''}}{i} = \dfrac{{D - 30}}{D} = \dfrac{{50 - 30}}{{50}} = \dfrac{2}{5} = \dfrac{{\dfrac{{{x_M}}}{k}}}{{\dfrac{{{x_M}}}{4}}} = \dfrac{4}{k} \Rightarrow k = 10\) Vậy tại M có vân sáng bậc 10
Câu 24 :
Chiếu xiên từ không khí vào nước một chùm sáng song song rất hẹp (coi như một tia sáng) gồm ba thành phần đơn sắc: cam, lục và chàm. Gọi \({r_{cam}},{r_{luc}},{r_{cham}}\) lần lượt là góc khúc xạ ứng với tia màu cam, tia màu lục và tia màu chàm. Hệ thức đúng là:
Đáp án : B Phương pháp giải :
+ Sử dụng tính chất chiết suất của ánh sáng trong các chất trong suốt: \(\left( {{n_{do}} < {n_{cam}} < {n_{vang}} < {n_{luc}} < {n_{lam}} < {n_{cham}} < {n_{tim}}} \right)\) + Vận dụng lí thuyết về khúc xạ ánh sáng: Ánh sáng đi từ môi trường chiết quang kém sang môi trường chiết quang hơn thì tia khúc xạ gần pháp tuyến hơn so với tia tới Lời giải chi tiết :
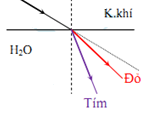
Ta có: + Chiết suất của các chất trong suốt biến thiên theo màu sắc của ánh sáng và tăng dần từ màu đỏ đến màu tím \(\left( {{n_{do}} < {n_{cam}} < {n_{vang}} < {n_{luc}} < {n_{lam}} < {n_{cham}} < {n_{tim}}} \right)\) + Theo định luật khúc xạ ánh sáng: Ánh sáng đi từ môi trường chiết quang kém sang môi trường chiết quang hơn thì tia khúc xạ gần pháp tuyến hơn so với tia tới, ta có hình ảnh khúc xạ của các tia sáng:
Tia tím xa phương truyền ban đầu nhất, tia đỏ gần phương truyền ban đầu nhất => Ánh sáng từ đỏ đến tím có góc lệch so với phương truyền ban đầu giảm dần hay góc khúc xạ tăng dần từ tím đến đỏ: rđỏ > rcam > rvàng > rlục > rlam > rchàm > rtím => \({r_{cham}} < {r_{luc}} < {\rm{ }}{r_{cam}}\)
Câu 25 :
Trong một thí nghiệm Y-âng về giao thoa ánh sáng, khoảng cách giữa hai khe là 0,8 mm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là 1,6 m. Nguồn sáng phát ánh sáng trắng có bước sóng trong khoảng từ 380 nm đến 760 nm. M là một điểm trên màn, cách vân sáng trung tâm 1 cm. Trong các bước sóng của các bức xạ cho vân sáng tại M, bước sóng ngắn nhất là
Đáp án : B Phương pháp giải :
+ Sử dụng lí thuyết về giao thoa ánh sáng trắng và công thức xác định vị trí vân sáng + Vị trí vân sáng: \({x_s} = \dfrac{{k\lambda D}}{a}\) Lời giải chi tiết :
Vị trí điểm M: \({x_M} = 10mm = \dfrac{{k\lambda D}}{a} \\\Rightarrow \lambda = \dfrac{5}{k}\mu m\) Mà: Bước sóng ngắn nhất ứng với k lớn nhất \(= 13\) \( \Rightarrow \lambda = \dfrac{5}{{13}} = 0,385\mu m = 385nm\)
Câu 26 :
Trong thí nghiệm Y-âng về giao thoa ánh sáng, khoảng cách giữa hai khe là 1mm, khoảng cách từ hai khe đến màn là 1,2m. Nguồn S phát áng sáng trắng có bước sóng trong khoảng \(0,4\mu m \le \lambda \le 0,76\mu m\). Tần số lớn nhất của bức xạ đơn sắc cho vân sáng tại điểm M trên màn cách vân trung tâm một đoạn 2,1mm là
Đáp án : A Phương pháp giải :
Sử dụng lí thuyết giao thoa ánh sáng Vị trí vân sáng: \({x_s} = k\dfrac{{\lambda D}}{a}\) Lời giải chi tiết :
+ M cách vân trung tâm đoạn 2,1 mm cho vân sáng \(\begin{array}{l}{x_M} = k\dfrac{{\lambda D}}{a}\\ \Rightarrow \lambda = \dfrac{{{x_M}a}}{{kD}} = \dfrac{{2,1.1}}{{1,2k}} = \dfrac{{1,75}}{k}\left( {\mu m} \right)(k \in Z)\end{array}\) + Mà bước sóng nằm trong khoảng \(0,4\mu m \le \lambda \le 0,76\mu m\) \(\begin{array}{l}0,4 \le \dfrac{{1,75}}{k} \le 0,76\\ \Rightarrow 2,3 \le k \le 4,375\\ \Rightarrow k = 3,4\end{array}\) => Tần số lớn nhất của bức xạ cho vân sáng tại M, ứng với bước sóng ngắn nhất (k = 4) \(\begin{array}{l}{\lambda _{\min }}\left( {k = 4} \right) = \dfrac{{1,75}}{4} = 0,4375\mu m\\ \Rightarrow {f_{max}} = \dfrac{c}{{{\lambda _{\min }}}} = \dfrac{{{{3.10}^8}}}{{{{0,4375.10}^{ - 6}}}} = {6,86.10^{14}}Hz\end{array}\)
Câu 27 :
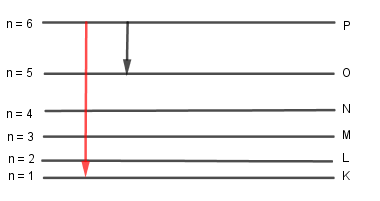
Theo mẫu nguyên tử Bo, mức năng lượng của trạng thái dừng thứ n của nguyên tử Hidro được xác định theo công thức \({E_n} = - \dfrac{{13,6}}{{{n^2}}}\left( {eV} \right);\left( {n = 1,2,3...} \right)\) Gọi R1 là bán kính quỹ đạo của e khi nguyên tử Hidro ở tạng thái dừng L. Khi nguyên tử ở trạng thái dừng ứng với bán kính bằng 9R1 thì tỷ số bước sóng lớn nhất và bước sóng nhỏ nhất của photon mà nguyên tử Hidro có thể phát xạ là:
Đáp án : D Phương pháp giải :
Áp dụng công thức xác định mức năng lượng của photon: \({E_n} = - \dfrac{{13,6}}{{{n^2}}}\left( {eV} \right);\left( {n = 1,2,3...} \right)\) Lời giải chi tiết :
R1 là bán kính quỹ đạo e ứng với trạng thái dừng L vậy \({r_1} = {2^2}{r_0}\) Khi bán kính quỹ đạo là 9R1 ta có \(r = 9{r_1} = 9.4{r_0} = 36{r_0} = > n = 6\) ứng với trạng thái dừng P Bước sóng lớn nhất mà photon này có thể phát xạ ra khi nó chuyển mức năng lượng từ trạng thái P về trạng thái K là \(E = {E_P} - {E_0} = \dfrac{{{E_0}}}{{{6^2}}} - {E_0} = \dfrac{{35}}{{36}}{E_0} = \dfrac{{hc}}{{{\lambda _{max}}}} = > {\lambda _{max}} = \dfrac{{hc}}{{\dfrac{{35}}{{36}}{E_0}}}\) Bước sóng ngắn nhất photon này có thể phát xạ ra khi nó chuyển mức năng lượng từ trạng thái P về trạng thái O là \(E = {E_P} - {E_O} = \dfrac{{{E_0}}}{{{6^2}}} - \dfrac{{{E_0}}}{5} = \dfrac{{11}}{{900}}{E_0} = \dfrac{{hc}}{{{\lambda _{\min }}}} = > {\lambda _{\min }} = \dfrac{{hc}}{{\dfrac{{11}}{{900}}{E_0}}}\) Tỷ số giữa bước sóng ngắn lớn nhất và dài nhất là \(\dfrac{{{\lambda _{\min }}}}{{{\lambda _{max}}}} = \dfrac{{\dfrac{{hc}}{{\dfrac{{35}}{{36}}{E_0}}}}}{{\dfrac{{hc}}{{\dfrac{{11}}{{900}}{E_0}}}}} = \dfrac{{35}}{{36}}.\dfrac{{900}}{{11}} = \dfrac{{875}}{{11}}\)
Câu 28 :
Một mạch dao động ở máy vào của một máy thu thanh gồm cuộn thuần cảm có độ tự cảm 3 µH và tụ điện có điện dung biến thiên trong khoảng từ 10 pF đến 500pF. Biết rằng, muốn thu được sóng điện từ thì tần số riêng của mạch dao động phải bằng tần số của sóng điện từ cần thu (để có cộng hưởng). Trong không khí, tốc độ truyền sóng điện từ là 3.108 m/s, máy thu này có thể thu được sóng điện từ có bước sóng trong khoảng
Đáp án : B Phương pháp giải :
Áp dụng công thức tính bước sóng của sóng điện từ: \(\lambda = 2\pi c\sqrt {LC} \) Lời giải chi tiết :
Áp dụng công thức: \(\lambda = 2\pi c\sqrt {LC} \). Ta có: \(\left\{ \begin{array}{l}{\lambda _{\min }} = 2\pi .c\sqrt {L{C_{\min }}} = 2.3,{14.3.10^8}\sqrt {{{3.10}^{ - 6}}{{.10.10}^{ - 12}}} \approx 10,319m.\\{\lambda _{max}} = 2\pi .c\sqrt {L{C_{max}}} = 2.3,{14.3.10^8}\sqrt {{{3.10}^{ - 6}}{{.500.10}^{ - 12}}} \approx 72,967m.\end{array} \right.\) => máy thu này có thể thu được sóng điện từ có bước sóng trong khoảng từ 10m đến 73m
Câu 29 :
Một mạch dao động lí tưởng gồm cuộn cảm thuần có độ tự cảm L không đổi và tụ điện có điện dung C thay đổi được. Điều chỉnh điện dung của tụ điện đến giá trị C1 thì tần số dao động riêng của mạch là f1. Để tần số dao động riêng của mạch là \(\sqrt 5 {f_1}\) thì phải điều chỉnh điện dung của tụ điện đến giá trị
Đáp án : A Phương pháp giải :
Áp dụng công thức tính tần số dao động của mạch LC: \(f = \dfrac{1}{{2\pi \sqrt {LC} }}\) Lời giải chi tiết :
\(f = \dfrac{1}{{2\pi \sqrt {LC} }} \Rightarrow \dfrac{{{C_2}}}{{{C_1}}} = \dfrac{{f_1^2}}{{f_2^2}} = \dfrac{1}{5} = > {C_2} = \dfrac{{{C_1}}}{5} = 0,2{C_1}\)
Câu 30 :
Trong mạch dao động lí tưởng đang có dao động điện từ tự do với chu kỳ T. Biết tụ điện có điện dung \(2nF\) và cuộn cảm có độ tự cảm \(8mH\). Tại thời điểm t1, cường độ dòng điện trong mạch có độ lớn \(5 mA\). Tại thời điểm t2 = t1 + 2π.10-6(s) điện áp giữa hai bản tụ có độ lớn
Đáp án : A Phương pháp giải :
Chu kỳ mạch dao động LC là: \(T = 2\pi \sqrt {LC} \) Liên hệ giữa điện áp cực đại và dòng điện cực đại: \(CU_0^2 = LI_0^2\) Điện tích cực đại q0 = CU0 Mạch LC có u và i vuông pha nhau Lời giải chi tiết :
Chu kỳ mạch dao động LC là: \(T = 2\pi \sqrt {LC} = 2\pi \sqrt {{{8.10}^{ - 3}}{{.2.10}^{ - 9}}} = 8\pi {.10^{ - 6}}(s) \Rightarrow \omega = 2,{5.10^5}rad/s\) Ta có: \(CU_0^2 = LI_0^2 \Rightarrow {U_0} = \sqrt {\dfrac{{LI_0^2}}{C}} = 2000{I_0}\) ZL = 2000Ω; ZC = 2000Ω nên u và i cùng pha nhau Ở thời điểm t1 có i1 = ωq0cos(ωt1) = ωCU0cos(ωt1) = 5mA Ở thời điểm t2 có u2 = \({U_0}{\rm{cos}}\left[ {\omega ({t_1} + \dfrac{T}{4}) - \dfrac{\pi }{2}} \right] = {U_0}{\rm{cos}}\omega {{\rm{t}}_1} = \dfrac{{{i_1}}}{{\omega C}} = \dfrac{{{{5.10}^{ - 3}}}}{{2,{{5.10}^5}{{.2.10}^{ - 9}}}} = 10V\)
Câu 31 :
Để truyền thông tin liên lạc bằng sóng vô tuyến, người ta sử dụng phương pháp biến điệu biên độ, trong đó sóng cao tần có tần số \(800 kHz\) và sóng âm tần có tần số \(1 kHz\). Tần số của sóng sau khi biến điệu là
Đáp án : D Phương pháp giải :
Tần số của sóng sau khi biến điệu là tần số của sóng cao tần Lời giải chi tiết :
Tần số của sóng sau khi biến điệu là tần số của sóng cao tần: \(800 kHz\)
Câu 32 :
Trong chân không, ánh sáng nhìn thấy được có bước sóng trong khoảng từ
Đáp án : A Phương pháp giải :
Vận dụng thang sóng điện từ Lời giải chi tiết :
Trong chân không, ánh sáng nhìn thấy được có bước song trong khoảng \(0,38 µm\) đến \(0,76 µm\).
Câu 33 :
Gọi nđ, nt và nv lần lượt là chiết suất của một môi trường trong suốt đối với các ánh sáng đơn sắc đỏ, tím và vàng. Sắp xếp nào sau đây là đúng?
Đáp án : C Lời giải chi tiết :
Chiết suất của một môi trường trong suốt đối với ánh sáng đơn sắc tím lớn hơn vàng, lớn hơn đỏ. nt > nv > nđ.
Câu 34 :
Trong thí nghiệm Y‒âng về giao thoa ánh sáng, người ta sử dụng nguồn phát ánh sáng trắng có bước sóng từ \(400 nm\) đến \(760 nm\). Trên màn quan sát, \(M\) là vị trí mà tại đó có đúng \(6\) bức xạ cho vân sáng, trong đó có vân sáng của hai bức xạ có bước sóng là \(680 nm\) và \(544 nm\). Tại \(M\) cũng là vị trí vân tối của một số bức xạ khác trong đó bức xạ có bước sóng ngắn nhất là \({\lambda _{min}}\). Giá trị \({\lambda _{min}}\) gần nhất với giá trị nào sau đây?
Đáp án : A Phương pháp giải :
Tại vị trí n các vân sáng trùng nhau ,có n giá trị thỏa mãn: \({k_1}{\lambda _1} = k\lambda \) Tại vị trí cho vân sáng: x=ki Tại vị trí cho vân tối : x=(m+0,5)i Lời giải chi tiết :
+ \(\dfrac{{{k_1}}}{{{k_2}}} = \dfrac{{{\lambda _2}}}{{{\lambda _1}}} = \dfrac{{544}}{{680}} = \dfrac{4}{5} = \dfrac{8}{{10}} = \dfrac{{12}}{{15}} = ...\) + \({k_1}{\lambda _1} = k\lambda \) \({k_1} = 4 \to 400 \le \lambda = \dfrac{{{k_1}{\lambda _1}}}{k} = \dfrac{{4.680}}{k} \le 760 \to 3,58 \le k \le 6,8 \to k = 4,5,6(loai)\) \({k_1} = 8 \to 400 \le \lambda = \dfrac{{{k_1}{\lambda _1}}}{k} = \dfrac{{8.680}}{k} \le 760 \to 7,16 \le k \le 13,6(*) \to k = \underbrace {8,9,10,11,12,13}_{co6giatri \to co6bucxa}\) + Vị trí M: x=8.i1 + Tại M cũng là vị trí vân tối của một số bức xạ khác => \(x = 8.{i_1} = (m + \dfrac{1}{2})i' \to \lambda ' = \dfrac{{8.{\lambda _1}}}{{(m + \dfrac{1}{2})}}\) Mà \(400 \le \lambda ' \le 760 \to 400 \le \dfrac{{8.{\lambda _1}}}{{(m + \dfrac{1}{2})}} \le 760 \to 6,6 \le m \le 13,1\) à \({\lambda _{\min }} = \dfrac{{8.680}}{{13,5}} \approx \)\(402,962963(nm)\)
Câu 35 :
Một mạch dao động có tụ điện với điện dung \(C = 6pF\), cuộn cảm có hệ số tự cảm \(L = 2,4mH\) và điện trở hoạt động \(R = 5\Omega \). Để duy trì dao động của mạch như ban dầu thì cần nguồn cung cấp cho mạch có công suất \(45\mu W\). Hiệu điện thế cực đại trên tụ là?
Đáp án : D Phương pháp giải :
Sử dụng các công thức xác định: + Công suất cần cung cấp để duy trì dao động của mạch: \(P = \dfrac{Q}{t} = \dfrac{{{I^2}Rt}}{t} = {I^2}R = \dfrac{{I_0^2}}{2}R\) + Cường độ dòng điện cực đại trong mạch: \({I_0} = {U_0}\sqrt {\dfrac{C}{L}} \) Lời giải chi tiết :
Ta có: + Công suất cần cung cấp để duy trì dao động của mạch: \(\begin{array}{l}P = \dfrac{Q}{t} = \dfrac{{{I^2}Rt}}{t} = {I^2}R = \dfrac{{I_0^2}}{2}R\\ \Rightarrow I_0^2 = \dfrac{{2P}}{R} = \dfrac{{{{2.4,5.10}^{ - 5}}}}{5} = {1,8.10^{ - 5}}\\ \Rightarrow {I_0} = 3\sqrt 2 {.10^{ - 3}}A\end{array}\) + Mặt khác, ta có: \(L{I_0}^2 = C{U_0}^2 \to {U_0} = {I_0}\sqrt {\dfrac{L}{C}} = 3\sqrt 2 {.10^{ - 3}}.\sqrt {\dfrac{{{{2,4.10}^{ - 3}}}}{{{{6.10}^{ - 12}}}}} = 60\sqrt 2 V\)
Câu 36 :
Một mạch dao động LC đang thu được sóng trung. Để mạch có thể thu được sóng dài thì phải
Đáp án : C Phương pháp giải :
+ Vận dụng lí thuyết về sóng trung và sóng dài + Vận dụng biểu thức tính bước sóng + Vận dụng lí thuyết về mạch có C nối tiếp, song song Lời giải chi tiết :
Ta có: + Sóng trung có bước sóng ngắn hơn sóng dài + Bước sóng: \(\lambda = 2\pi c\sqrt {LC} \) tỉ lệ thuận với \(\sqrt C ,\sqrt L \) => Mạch đang thu được sóng trung, để mạch có thể thu được sóng dài thì ta cần mắc thêm vào mạch một tụ điện có điện dung hoặc cuộn cảm có độ tự cảm thích hợp sao cho bước sóng của mạch tăng A- Khi mắc nối tiếp thêm tụ điện : \(\dfrac{1}{{{C_{nt}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} \to {C_{nt}} < {C_1} \to \lambda \downarrow \) không thỏa mãn B- Bước sóng không phụ thuộc vào điện trở => không thỏa mãn C- Khi mắc nối tiếp thêm cuộn cảm: \({L_{nt}} = {L_1} + {L_2} > {L_1} \to \lambda \uparrow \) thỏa mãn D- Khi mắc song song thêm cuộn cảm: \(\dfrac{1}{{{L_{//}}}} = \dfrac{1}{{{L_1}}} + \dfrac{1}{{{L_2}}} \to {L_{//}} < {L_1} \to \lambda \downarrow \) không thỏa mãn
Câu 37 :
Một máy thu thanh đang thu được sóng ngắn. Để chuyển sang thu sóng cực ngắn, có thể thực hiện giải pháp nào sau đây trong mạch dao động anten
Đáp án : A Phương pháp giải :
+ Vận dụng lí thuyết về sóng ngắn và sóng cực ngắn + Vận dụng biểu thức tính bước sóng Lời giải chi tiết :
Ta có: + Sóng ngắn có bước sóng dài hơn sóng cực ngắn + Bước sóng: \(\lambda = 2\pi c\sqrt {LC} \) tỉ lệ thuận với \(\sqrt C ,\sqrt L \) => Mạch đang thu được sóng ngắn, để mạch có thể thu được sóng cực ngắn thì ta cần mắc thêm vào mạch một tụ điện có điện dung hoặc cuộn cảm có độ tự cảm thích hợp sao cho bước sóng của mạch giảm A - Khi giảm C và giảm L => bước sóng giảm => thỏa mãn B - Khi giữ nguyên C và tăng L => bước sóng tăng => không thỏa mãn C - Khi tăng L và tăng C => bước sóng tăng => không thỏa mãn D- Khi giữ nguyên L và tăng C => bước sóng tăng => không thỏa mãn
Câu 38 :
Điện dung của tụ điện phải thay đổi trong khoảng nào để mạch có thể thu được sóng vô tuyến có bước sóng nằm trong khoảng từ \({\lambda _1}\) đến \({\lambda _2}\) (\({\lambda _1} < {\lambda _2}\)). Chọn kết quả đúng:
Đáp án : A Phương pháp giải :
Áp dụng biểu thức xác định bước sóng: \(\lambda = 2\pi c\sqrt {LC} \) Lời giải chi tiết :
Ta có: \(\lambda = 2\pi c\sqrt {LC} \Rightarrow C = \dfrac{{{\lambda ^2}}}{{4{\pi ^2}c^2L}}\) => Để mạch thu được sóng vô tuyến có bước sóng nằm trong khoảng từ \({\lambda _1}\) đến \({\lambda _2}\) (\({\lambda _1} < {\lambda _2}\)) thì tụ điện C phải: \(\dfrac{{\lambda _1^2}}{{4{\pi ^2}c^2L}} < C < \dfrac{{\lambda _2^2}}{{4{\pi ^2}c^2L}}\)
Câu 39 :
Trong mạch dao động LC có điện trở thuần bằng không thì năng lượng
Đáp án : C Lời giải chi tiết :
Trong mạch dao động LC thì năng lượng điện trường tập trung trong tụ điện và biến thiên với chu kì bằng một nửa chu kì dao động riêng của mạch.
Câu 40 :
Trong một thí nghiệm Y – âng về giao thoa ánh sáng, có a = 1mm, D = 2m. Nếu chiếu đồng thời hai bức xạ đơn sắc có bước sóng λ1 = 0,6μm; λ2 = 0,5μm thì trên màn quan sát có những vị trí tại đó có vân sáng của hai bức xạ trùng nhau gọi là vân trùng. Khoảng cách ngắn nhất giữa hai vân trùng bằng
Đáp án : B Phương pháp giải :
Công thức tính khoảng vân: \(i = \frac{{\lambda D}}{a}\) Vì có hai bức xạ nên ta có, tại vị trí có cùng lúc hai vân sáng của hai bức xạ thì: \({x_M} = {k_1}.{i_1} = {k_2}.{i_2} \Rightarrow \frac{{{i_1}}}{{{i_2}}} = \frac{{{\lambda _1}}}{{{\lambda _2}}} = \frac{{{k_2}}}{{{k_1}}} = \frac{a}{b}\) Với \(\frac{a}{b}\) là phân số tối giản thì khoảng vân trùng nhau là: \(i' = b{i_1} = a{i_2}\) Lời giải chi tiết :
Khoảng vân của hai bức xạ là: \(\left\{ \begin{array}{l} Vì có hai bức xạ nên ta có, tại vị trí có cùng lúc hai vân sáng của hai bức xạ thì: \({x_M} = {k_1}.{i_1} = {k_2}.{i_2} \Rightarrow \frac{{{i_1}}}{{{i_2}}} = \frac{{1,2}}{1} = \frac{6}{5}\) Với \(\frac{6}{5}\) là phân số tối giản thì khoảng vân trùng nhau là: \(i' = 5{i_1} = 6{i_2} = 6mm\) Vậy khoảng cách giữa hai vân trùng nhau liên tiếp là 6mm. |





















Danh sách bình luận