Đề kiểm tra 1 tiết chương 2: Sóng cơ và sóng âm - Đề số 03Đề bài
Câu 1 :
Một sóng ngang hình sin truyền trên một sợi dây dài. Chu kì của sóng cơ này là 3s. Ở thời điểm t, hình dạng một đoạn của sợi dây như hình vẽ. Các vị trí cân bằng của các phần tử dây cùng nằm trên trục Ox. Tốc độ lan truyền của sóng cơ này là: 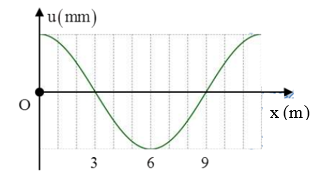
Câu 2 :
Âm nghe được là sóng cơ học có tần số nằm trong khoảng:
Câu 3 :
Phát biểu nào sau đây là đúng?
Câu 4 :
Sóng cơ có tần số $50 Hz$ truyền trong môi trường với vận tốc $160 m/s$. Ở cùng một thời điểm, hai điểm gần nhau nhất trên một phương truyền sóng có dao động cùng pha với nhau, cách nhau
Câu 5 :
Tại mặt chất lỏng có hai nguồn phát sóng \(A,{\rm{ }}B\) giống nhau và cách nhau một đoạn \(10{\rm{ }}cm\). Gọi \(M\)và \(N\) là hai điểm thuộc mặt chất lỏng sao cho \(MN{\rm{ }} = {\rm{ }}8{\rm{ }}cm\) và \(ABMN\) là hình thang cân (\(AB\) song song với \(MN\)). Bước sóng của sóng trên mặt chất lỏng do hai nguồn phát ra là \(1{\rm{ }}cm\). Để trong đoạn \(MN\) có \(7\) điểm dao động với biên độ cực đại thì diện tích lớn nhất của hình bình hành là:
Câu 6 :
Ở mặt chất lỏng có $2$ nguồn kết hợp đặt tại $A$ và $B$ dao động điều hòa, cùng pha theo phương thẳng đứng. $Ax$ là nửa đường thẳng nằm ở mặt chất lỏng và vuông góc với $AB$. Trên $Ax$ có những điểm mà các phần tử ở đó dao động với biên độ cực đại, trong đó $M$ là điểm xa $A$ nhất, $N$ là điểm kế tiếp với $M$, $P$ là điểm kế tiếp với $N$ và $Q$ là điểm gần $A$ nhất. Biết $MN = 22,25 cm$, $NP = 8,75 cm$. Độ dài đoạn $QA$ gần nhất với giá trị nào sau đây?
Câu 7 :
Trên một sợi dây \(AB\) dài \(1,2{\rm{ }}m\) đang có sóng dừng với \(3\) bụng sóng, biên độ bụng sóng \(a = 4\sqrt 2 cm\) . Tốc độ truyền sóng trên dây \(v{\rm{ }} = {\rm{ }}80{\rm{ }}cm/s\). Biết hai đầu \(A,{\rm{ }}B\) là các nút sóng. Ở thời điểm phần tử tại điểm \(M\) trên dây cách \(A\) \(30{\rm{ }}cm\) có li độ \(2{\rm{ }}cm\) thì phần tử tại điểm \(N\) trên dây cách \(B\) \(50{\rm{ }}cm\) có tốc độ là:
Câu 8 :
Cường độ âm tại một điểm trong môi trường truyền âm là \({10^{ - 5}}W/{m^2}\). Biết cường độ âm chuẩn là \({10^{ - 12}}W/{m^2}\). Mức cường độ âm tại điểm đó bằng:
Câu 9 :
Ở mặt nước có hai nguồn kết hợp \(A,{\rm{ }}B\) dao động theo phương thẳng đứng với phương trình \({u_A} = {\rm{ }}{u_B} = {\rm{ }}4cos\left( {\omega t} \right){\rm{ }}\left( {mm} \right)\). Tốc độ truyền sóng và biên độ sóng không đổi khi sóng truyền đi. Phần tử \(M\) ở mặt nước thuộc vân giao thoa cực tiểu có biên độ dao động là:
Câu 10 :
Sóng cơ truyền được trong các môi trường:
Câu 11 :
Chọn câu sai.
Câu 12 :
Cho phương trình sóng: \(u = a\sin \left( {4\pi t + \frac{\pi }{4} - \frac{{2\pi x}}{3}} \right)\left( {m,s} \right)\). Phương trình này biểu diễn:
Câu 13 :
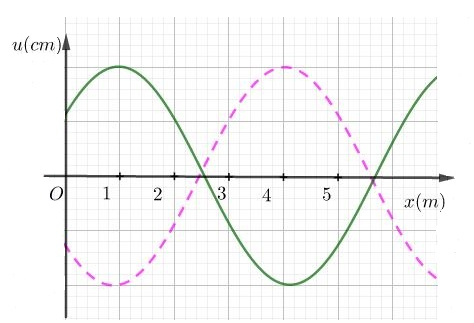
Một sóng cơ học tại thời điểm \(t{\rm{ }} = {\rm{ }}0\) có đồ thị là đường liền nét. Sau thời gian \(t\), nó có đồ thị là đường đứt nét. Cho biết vận tốc truyền sóng là 4m/s, sóng truyền từ phải qua trái. Giá trị của \(t\) là:
Câu 14 :
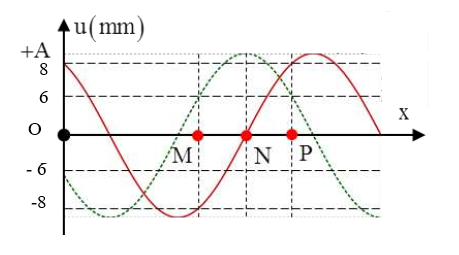
Trên một sợi dây đàn hồi có ba điểm M, N và P với N là trung điểm của đoạn MP. Trên dây có sóng lan truyền từ M đến B với chu kì \(T\) \(\left( {T > 0,5s} \right)\). Hình vẽ bên mô tả hình dạng của sợi dây ở thời điểm \({t_1}\) (nét liền) và \({t_2} = {t_1} + 0,5s\) (nét đứt). M, N và P lần lượt là các vị trí cân bằng tương ứng. Coi biên độ sóng không đổi khi truyền đi. Tại thời điểm \({t_0} = {t_1} - \dfrac{1}{9}s\) vận tốc của phần tử dây tại N là:
Câu 15 :
Hai sóng kết hợp là hai sóng:
Câu 16 :
Tại hai điểm A và B trên mặt nước nằm ngang có hai nguồn sóng cơ kết hợp, dao động theo phương thẳng đứng. Có sự giao thoa của hai sóng này trên mặt nước. Tại trung điểm của đoạn AB, phần tử nước dao động với biên độ cực tiểu. Hai nguồn sóng đó dao động:
Câu 17 :
Quan sát sóng dừng trên một sợi dây đàn hồi, người ta đo được khoảng cách giữa \(3\) nút sóng liên tiếp là \(100cm\). Biết tần số của sóng truyền trên dây bằng \(50Hz\), vận tốc truyền sóng trên dây là:
Câu 18 :
Khi có sóng dừng trên dây, khoảng cách từ một bụng đến nút gần nó nhất bằng bao nhiêu? Biết sóng truyền trên dây có bước sóng \(\lambda = 4m\)
Câu 19 :
Quan sát trên một sợi dây thấy có sóng dừng với biên độ của bụng sóng là a. Tại điểm trên sợi dây cách bụng sóng một phần ba bước sóng có biên độ dao động bằng:
Câu 20 :
Một người đứng cách một bức tường 30 m nghe một tiếng súng nổ. Vị trí đặt súng cách tường 165 m. Người và súng cùng trên đường thẳng vuông góc với tường. Sau khi nghe tiếng nổ, người này lại nghe tiếng nổ do âm thanh phản xạ trên bức tường. Tốc độ âm thanh trong không khí là 330 m/s. Khoảng thời gian giữa hai tiếng nổ là:
Câu 21 :
Thuật ngữ âm “trầm” , “bổng” chỉ đặc tính nào của âm dưới đây?
Câu 22 :
Ở bề mặt một chất lỏng có hai nguồn phát sóng kết hợp \({S_1}\) và \({S_2}\) cách nhau \(15cm\). Hai nguồn này dao động theo phương thẳng đứng có phương trình lần lượt là \({u_1} = 5cos50\pi t\left( {mm} \right)\) và \({u_2} = 5cos(50\pi t + \pi ){\rm{ }}\left( {mm} \right)\). Tốc độ truyền sóng trên mặt chất lỏng là \(120cm/s\). Xét các điểm trên \({S_1}{S_2}\). Gọi I là trung điểm của \({S_1}{S_2}\); M nằm cách I một đoạn 3cm sẽ dao động với biên độ:
Câu 23 :
Sóng cơ truyền dọc theo trục Ox có phương trình \(u = 4cos(50πt – 0,125x) (mm)\). Tần số của sóng này bằng :
Câu 24 :
Ở mặt nước, tại hai điểm A và B cách nhau \(19 cm\), có hai nguồn kết hợp dao động cùng pha theo phương thẳng đứng, phát ra hai sóng có bước sóng \(4 cm\). Trong vùng giao thoa, M là một điểm ở mặt nước thuộc đường trung trực của AB. Trên đoạn AM, số điểm cực tiểu giao thoa là
Câu 25 :
Sóng dọc là sóng có phương dao động của các phần tử môi trường và phương truyền sóng hợp với nhau một góc
Lời giải và đáp án
Câu 1 :
Một sóng ngang hình sin truyền trên một sợi dây dài. Chu kì của sóng cơ này là 3s. Ở thời điểm t, hình dạng một đoạn của sợi dây như hình vẽ. Các vị trí cân bằng của các phần tử dây cùng nằm trên trục Ox. Tốc độ lan truyền của sóng cơ này là: 
Đáp án : D Phương pháp giải :
+ Sử dụng phương pháp đọc đồ thị dao động sóng + Áp dụng công thức tính tốc độ lan truyền sóng: \(v = \frac{\lambda }{T}\) Lời giải chi tiết :
Từ đồ thị ta có: \(\frac{\lambda }{2} = 9 - 3 = 6 \to \lambda = 12m\) Tốc độ lan truyền sóng: \(v = \frac{\lambda }{T} = \frac{{12}}{3} = 4m/s\)
Câu 2 :
Âm nghe được là sóng cơ học có tần số nằm trong khoảng:
Đáp án : A Lời giải chi tiết :
Âm nghe được (âm thanh) là sóng cơ học có tần số nằm trong khoảng $16 Hz- 20000 Hz$
Câu 3 :
Phát biểu nào sau đây là đúng?
Đáp án : D Lời giải chi tiết :
Hai sóng là hai sóng kết hợp tức là hai sóng cùng tần số và có độ lệch pha không đổi theo thời gian (hoặc hai sóng cùng pha).
Câu 4 :
Sóng cơ có tần số $50 Hz$ truyền trong môi trường với vận tốc $160 m/s$. Ở cùng một thời điểm, hai điểm gần nhau nhất trên một phương truyền sóng có dao động cùng pha với nhau, cách nhau
Đáp án : A Phương pháp giải :
Áp dụng biểu thức tính bước sóng: \(\lambda = vT\) Lời giải chi tiết :
Ta có bước sóng: \(\lambda = \dfrac{v}{f} = \dfrac{{160}}{{50}} = 3,2m\) Khoảng cách giữa hai điểm gần nhau nhất trên một phương truyền sóng dao động cùng pha với nhau là 1 bước sóng.
Câu 5 :
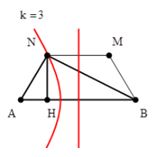
Tại mặt chất lỏng có hai nguồn phát sóng \(A,{\rm{ }}B\) giống nhau và cách nhau một đoạn \(10{\rm{ }}cm\). Gọi \(M\)và \(N\) là hai điểm thuộc mặt chất lỏng sao cho \(MN{\rm{ }} = {\rm{ }}8{\rm{ }}cm\) và \(ABMN\) là hình thang cân (\(AB\) song song với \(MN\)). Bước sóng của sóng trên mặt chất lỏng do hai nguồn phát ra là \(1{\rm{ }}cm\). Để trong đoạn \(MN\) có \(7\) điểm dao động với biên độ cực đại thì diện tích lớn nhất của hình bình hành là:
Đáp án : C Phương pháp giải :
Sử dụng điều kiện có cực đại giao thoa trong giao thoa sóng hai nguồn cùng pha \({d_2}-{\rm{ }}{d_1} = {\rm{ }}k\lambda \) Lời giải chi tiết :
Để diện tích $ABMN$ là lớn nhất thì $AH$ phải lớn nhất điều này xảy ra khi $N$ nằm tên cực đại thứ $3$ Ta có: \(\begin{array}{l}\left\{ \begin{array}{l}NB - NA = 3\lambda \\N{B^2} = N{H^2} + {9^2}\\N{A^2} = N{H^2} + 1\end{array} \right.\\ \Rightarrow \sqrt {N{H^2} + 9} - \sqrt {N{H^2} + 1} = 3cm\\ \Rightarrow NH = 11,8cm\end{array}\) Diện tích $ABMN$ khi đó là: \(S = \dfrac{1}{2}\left( {AB + MN} \right)NH = \dfrac{1}{2}\left( {10 + 8} \right)11,8 = 106,2c{m^2}\)
Câu 6 :
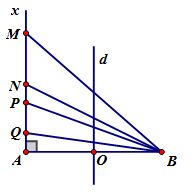
Ở mặt chất lỏng có $2$ nguồn kết hợp đặt tại $A$ và $B$ dao động điều hòa, cùng pha theo phương thẳng đứng. $Ax$ là nửa đường thẳng nằm ở mặt chất lỏng và vuông góc với $AB$. Trên $Ax$ có những điểm mà các phần tử ở đó dao động với biên độ cực đại, trong đó $M$ là điểm xa $A$ nhất, $N$ là điểm kế tiếp với $M$, $P$ là điểm kế tiếp với $N$ và $Q$ là điểm gần $A$ nhất. Biết $MN = 22,25 cm$, $NP = 8,75 cm$. Độ dài đoạn $QA$ gần nhất với giá trị nào sau đây?
Đáp án : C Phương pháp giải :
Sử dụng điều kiện cực đại của hai nguồn cùng pha: \({d_2} - {d_1} = k\lambda \) Lời giải chi tiết :
+ Ta thấy trên nửa đường thẳng kẻ từ \(A\) vuông góc với \(AB\) có \(4\) điểm theo thứ tự \(M,N,P,Q\) dao động với biên độ cực đại => Nên \(AB\) có \(9\) điểm dao động với biên độ cực đại với: \( - 4 \le k \le 4\left( {{d_2} - {d_1} = k\lambda } \right)\) Cực đại \(M,N,P,Q\) ứng với \(k = 1,2,3,4\) + Đặt \(AB = a\) Tại \(C\) trên $Ax$ là điểm dao động với biên độ cực đại: \(CB - CA = k\lambda \left( * \right)\) \(\begin{array}{l}C{B^2} - C{A^2} = {a^2}\\ \to \left( {CB - CA} \right)\left( {CB + CA} \right) = {a^2}\\ \to CB + CA = \dfrac{{{a^2}}}{{k\lambda }}\left( {**} \right)\end{array}\) Từ \(\left( * \right)\) và \(\left( {**} \right)\) ta suy ra: \(CA = \dfrac{{{a^2}}}{{2k\lambda }} - \dfrac{{k\lambda }}{2}\) - Tại \(M\) ứng với \(k = 1\): \(MA = \dfrac{{{a^2}}}{{2\lambda }} - \dfrac{\lambda }{2}\left( 1 \right)\) - Tại \(N\) ứng với \(k = 2\): \(NA = \dfrac{{{a^2}}}{{2.2\lambda }} - \dfrac{{2\lambda }}{2} = \dfrac{{{a^2}}}{{4\lambda }} - \lambda \left( 2 \right)\) - Tại \(P\) ứng với \(k = 3\): \(PA = \dfrac{{{a^2}}}{{2.3\lambda }} - \dfrac{{3\lambda }}{2} = \dfrac{{{a^2}}}{{6\lambda }} - \dfrac{{3\lambda }}{2}\left( 3 \right)\) - Tại \(Q\) ứng với \(k = 4\): \(QA = \dfrac{{{a^2}}}{{2.4\lambda }} - \dfrac{{4\lambda }}{2} = \dfrac{{{a^2}}}{{8\lambda }} - 2\lambda \left( 4 \right)\) Lấy \(\left( 1 \right) - \left( 2 \right)\) ta được: \(MN = MA - NA = \dfrac{{{a^2}}}{{4\lambda }} + \dfrac{\lambda }{2} = 22,25cm\left( 5 \right)\) Lấy \(\left( 2 \right) - \left( 3 \right)\) ta được: \(NP = NA - PA = \dfrac{{{a^2}}}{{12\lambda }} + \dfrac{\lambda }{2} = 8,75cm\left( 6 \right)\) Lấy \(3.\left( 6 \right) - \left( 5 \right)\) ta được: \(\begin{array}{l}3\left( {\dfrac{{{a^2}}}{{12\lambda }} + \dfrac{\lambda }{2}} \right) - \left( {\dfrac{{{a^2}}}{4} + \dfrac{\lambda }{2}} \right) = 3.8,75 - 22,25\\ \to \lambda = 4cm\end{array}\) Lấy \(\left( 5 \right) - \left( 6 \right)\) ta được: \(\dfrac{{{a^2}}}{{6\lambda }} = 22,25 - 8,75 = 13,5cm \to \dfrac{{{a^2}}}{\lambda } = 81cm\) Thay \(\left\{ \begin{array}{l}\lambda = 4cm\\\dfrac{{{a^2}}}{\lambda } = 81cm\end{array} \right.\) vào \(\left( 4 \right)\) ta được: \(QA = \dfrac{{{a^2}}}{{8\lambda }} - 2\lambda = \dfrac{{81}}{8} - 2.4 = 2,125cm\)
Câu 7 :
Trên một sợi dây \(AB\) dài \(1,2{\rm{ }}m\) đang có sóng dừng với \(3\) bụng sóng, biên độ bụng sóng \(a = 4\sqrt 2 cm\) . Tốc độ truyền sóng trên dây \(v{\rm{ }} = {\rm{ }}80{\rm{ }}cm/s\). Biết hai đầu \(A,{\rm{ }}B\) là các nút sóng. Ở thời điểm phần tử tại điểm \(M\) trên dây cách \(A\) \(30{\rm{ }}cm\) có li độ \(2{\rm{ }}cm\) thì phần tử tại điểm \(N\) trên dây cách \(B\) \(50{\rm{ }}cm\) có tốc độ là:
Đáp án : A Phương pháp giải :
+ Sử dụng điều kiện sóng dừng trên dây hai đầu cố định : \(l = k\dfrac{\lambda }{2}\) + Sử dụng biểu thức tính biên độ sóng dừng : \(A = 2a\left| {\sin \dfrac{{2\pi d}}{\lambda }} \right|\) + Vận dụng biểu thức tính bước sóng : \(\lambda = \dfrac{v}{f}\) + Sử dụng hệ thức độc lập A – x – v : \({A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}\) Lời giải chi tiết :
Điều kiện sóng dừng với hai đầu dây cố định : $\ell = \dfrac{{k\lambda }}{2} \Rightarrow \lambda = 80cm\left( {k = 3} \right)$ $ \Rightarrow f = \dfrac{v}{\lambda } = 1Hz \Rightarrow \omega = 2\pi rad/s$ Biên độ của một điểm cách nút một khoảng d là : \(A = 2a\left| {\sin \dfrac{{2\pi d}}{\lambda }} \right| \to \left\{ \begin{array}{l}{A_M} = 4cm\\{A_N} = 4cm\end{array} \right.\) Do \({A_M} = {\rm{ }}{A_N}\) Lại có: \({A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}\) => Tốc độ \(\left| {{v_M}} \right| = \left| {{v_N}} \right| = \omega \sqrt {A_M^2 - x_M^2} = 2\pi \sqrt {{4^2} - {2^2}} = 4\pi \sqrt 3 cm/s\)
Câu 8 :
Cường độ âm tại một điểm trong môi trường truyền âm là \({10^{ - 5}}W/{m^2}\). Biết cường độ âm chuẩn là \({10^{ - 12}}W/{m^2}\). Mức cường độ âm tại điểm đó bằng:
Đáp án : D Phương pháp giải :
Áp dụng công thức tính mức cường độ âm: \(L = 10\log \frac{I}{{{I_0}}}\) Lời giải chi tiết :
Ta có, mức cường độ âm: \(L = \log \frac{I}{{{I_0}}} = \log \frac{{{{10}^{ - 5}}}}{{{{10}^{ - 12}}}} = 7B = 70dB\)
Câu 9 :
Ở mặt nước có hai nguồn kết hợp \(A,{\rm{ }}B\) dao động theo phương thẳng đứng với phương trình \({u_A} = {\rm{ }}{u_B} = {\rm{ }}4cos\left( {\omega t} \right){\rm{ }}\left( {mm} \right)\). Tốc độ truyền sóng và biên độ sóng không đổi khi sóng truyền đi. Phần tử \(M\) ở mặt nước thuộc vân giao thoa cực tiểu có biên độ dao động là:
Đáp án : B Lời giải chi tiết :
Những điểm thuộc vân giao thoa cực tiểu có biên độ dao động bằng 0
Câu 10 :
Sóng cơ truyền được trong các môi trường:
Đáp án : D Lời giải chi tiết :
Sóng cơ chỉ truyền được trong các môi trường rắn , lỏng, khí
Câu 11 :
Chọn câu sai.
Đáp án : B Lời giải chi tiết :
A, C, D - đúng B - sai vì: Quá trình truyền sóng cơ là quá trình truyền các dao động, không phải là quá trình truyền các phần tử môi trường.
Câu 12 :
Cho phương trình sóng: \(u = a\sin \left( {4\pi t + \frac{\pi }{4} - \frac{{2\pi x}}{3}} \right)\left( {m,s} \right)\). Phương trình này biểu diễn:
Đáp án : C Phương pháp giải :
+ Đọc các đại lượng trong phương trình dao động sóng + Áp dụng công thức: \(\frac{{2\pi x}}{\lambda }\) + Áp dụng công thức tính vận tốc truyền sóng: \(v = \lambda f\) Lời giải chi tiết :
+ Ta có: \(u = a\sin \left( {4\pi t + \frac{\pi }{4} - \frac{{2\pi x}}{3}} \right)\left( {m,s} \right)\) => Sóng chạy theo chiều dương của trục x \(\frac{{2\pi x}}{\lambda } = \frac{{2\pi x}}{3} \to \lambda = 3m\) + Vận tốc truyền sóng: \(v = \lambda f = \lambda \frac{\omega }{{2\pi }} = 3.\frac{{4\pi }}{{2\pi }} = 6m/s\)
Câu 13 :
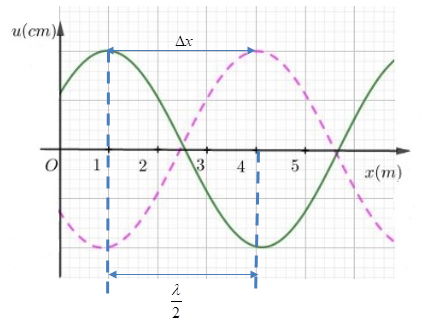
Một sóng cơ học tại thời điểm \(t{\rm{ }} = {\rm{ }}0\) có đồ thị là đường liền nét. Sau thời gian \(t\), nó có đồ thị là đường đứt nét. Cho biết vận tốc truyền sóng là 4m/s, sóng truyền từ phải qua trái. Giá trị của \(t\) là:
Đáp án : C Phương pháp giải :
+ Sử dụng phương pháp đọc đồ thị dao động sóng + Áp dụng biểu thức tính chu kì dao động sóng: \(T = \frac{\lambda }{v}\) + Vận dung lí thuyết về phương truyền sóng. Lời giải chi tiết :
Từ đồ thị, ta có: \(\frac{\lambda }{2} = 4 - 1 = 3m \to \lambda = 6m\) Chu kì dao động: \(T = \frac{\lambda }{v} = \frac{6}{4} = 1,5{\rm{s}}\) Khoảng cách giữa hai đỉnh sóng tại 2 thời điểm: \(\Delta x = 3m\) Mặt khác, ta có: \(v = \frac{{\Delta x}}{{\Delta t}} \to \Delta t = \frac{{\Delta x}}{v} = \frac{3}{4} = 0,75s\) => Sóng truyền từ phải qua trái \( \to t = 0,75s\)
Câu 14 :
Trên một sợi dây đàn hồi có ba điểm M, N và P với N là trung điểm của đoạn MP. Trên dây có sóng lan truyền từ M đến B với chu kì \(T\) \(\left( {T > 0,5s} \right)\). Hình vẽ bên mô tả hình dạng của sợi dây ở thời điểm \({t_1}\) (nét liền) và \({t_2} = {t_1} + 0,5s\) (nét đứt). M, N và P lần lượt là các vị trí cân bằng tương ứng. Coi biên độ sóng không đổi khi truyền đi. Tại thời điểm \({t_0} = {t_1} - \dfrac{1}{9}s\) vận tốc của phần tử dây tại N là:
Đáp án : D Phương pháp giải :
+ Đọc đồ thị và áp dụng các công thức sóng cơ học. + Viết phương trình dao động sóng + Áp dụng công thức tính khoảng cách giữa hai phần tử sóng: \(d = \sqrt {{x^2} + \Delta {u^2}} \) Lời giải chi tiết :
Từ đồ thị ta thấy rằng 2 thời điểm \({t_1}\) và \({t_2}\) vuông pha nhau, do đó: \(\begin{array}{l}\Delta \varphi = \omega \Delta t = \omega 0,5 = \left( {2k + 1} \right)\dfrac{\pi }{2}\\ \to \omega = \left( {2k + 1} \right)\pi ra{\rm{d}}/s\end{array}\) \(\begin{array}{l}{\left( {\dfrac{{{u_{1N}}}}{A}} \right)^2} + {\left( {\dfrac{{{u_{2N}}}}{A}} \right)^2} = 1\\ \to A = \sqrt {{u_{1N}}^2 + {u_{2N}}^2} = \sqrt {{{\left( 8 \right)}^2} + {{\left( { - 6} \right)}^2}} = 10mm\end{array}\) - Tại thời điểm t1 điểm N đang đi qua vị trí cân bằng theo chiều âm do vậy tốc độ của N sẽ là: \({v_{{N_1}}} = \omega A = 10\pi \left( {2k + 1} \right)mm/s\) - Vận tốc của N tại thời điểm \({t_0} = {t_1} - \dfrac{1}{9}s\) là \({v_{{N_0}}} = - {v_{{N_1}}}{\rm{cos}}\left( {2k + 1} \right)\dfrac{\pi }{9}mm/s\) Với k = 1 \( \to {v_{{N_0}}} = - 10\pi .3{\rm{cos}}\dfrac{{3\pi }}{9}mm/s = - 47,12mm/s = - 4,71cm/s\)
Câu 15 :
Hai sóng kết hợp là hai sóng:
Đáp án : C Lời giải chi tiết :
Hai sóng kết hợp là hai sóng do 2 nguồn kết hợp phát ra. Hai sóng kết hợp dao động cùng phương, cùng chu kì (hay tần số) và có hiệu số pha không đổi theo thời gian.
Câu 16 :
Tại hai điểm A và B trên mặt nước nằm ngang có hai nguồn sóng cơ kết hợp, dao động theo phương thẳng đứng. Có sự giao thoa của hai sóng này trên mặt nước. Tại trung điểm của đoạn AB, phần tử nước dao động với biên độ cực tiểu. Hai nguồn sóng đó dao động:
Đáp án : C Phương pháp giải :
+ Sử dụng công thức tính bước sóng: \(\lambda = \frac{v}{f}\) + Khoảng cách giữa 2 cực đại liên tiếp hoặc 2 cực tiểu liên tiếp là: \(\frac{\lambda }{2}\) Lời giải chi tiết :
Gọi I - trung điểm của AB Ta có: d1 = d2 (do I trung điểm AB) mà tại I dao động với biên độ cực tiểu => \(\Delta \varphi = \left( {2k + 1} \right)\pi \) => 2 nguồn ngược pha Chú ý
Tại I trung điểm của 2 nguồn sóng: - 2 nguồn cùng pha: I dao động với biên độ cực đại - 2 nguồn ngược pha: I dao động với biên độ cực tiểu
Câu 17 :
Quan sát sóng dừng trên một sợi dây đàn hồi, người ta đo được khoảng cách giữa \(3\) nút sóng liên tiếp là \(100cm\). Biết tần số của sóng truyền trên dây bằng \(50Hz\), vận tốc truyền sóng trên dây là:
Đáp án : A Phương pháp giải :
+ Vận dụng công thức xác định khoảng cách giữa n nút liền kề là \((n - 1)\frac{\lambda }{2}\) . + Vận dụng công thức tính vận tốc truyền sóng: \(v = \lambda f\) Lời giải chi tiết :
+ Khoảng cách giữa 3 nút liền kề là \(2\frac{\lambda }{2} = 100 \to \lambda = 100cm = 1m\) + Vận tốc truyền sóng: \(v = \lambda f = 1.50 = 50m/s\)
Câu 18 :
Khi có sóng dừng trên dây, khoảng cách từ một bụng đến nút gần nó nhất bằng bao nhiêu? Biết sóng truyền trên dây có bước sóng \(\lambda = 4m\)
Đáp án : B Lời giải chi tiết :
Ta có, khoảng cách giữa nút và bụng liền kề (gần nhất) là \(\frac{\lambda }{4} = \frac{4}{4} = 1m\)
Câu 19 :
Quan sát trên một sợi dây thấy có sóng dừng với biên độ của bụng sóng là a. Tại điểm trên sợi dây cách bụng sóng một phần ba bước sóng có biên độ dao động bằng:
Đáp án : A Phương pháp giải :
Sử dụng lí thuyết về phương trình sóng dừng: \({u_M} = 2Ac{\rm{os}}(2\pi \frac{d}{\lambda })c{\rm{os}}(2\pi ft)\) Lời giải chi tiết :
Ta có: \({A_M} = 2A\left| {{\rm{cos}}(2\pi \frac{d}{\lambda })} \right| = a\left| {{\rm{cos}}(2\pi \frac{d}{\lambda })} \right|\) Tại điểm cách bụng sóng một phần ba bước sóng có: \(d = \frac{\lambda }{3} \to {A_M} = a\left| {{\rm{cos}}(2\pi \frac{1}{3})} \right| = \frac{a}{2}\)
Câu 20 :
Một người đứng cách một bức tường 30 m nghe một tiếng súng nổ. Vị trí đặt súng cách tường 165 m. Người và súng cùng trên đường thẳng vuông góc với tường. Sau khi nghe tiếng nổ, người này lại nghe tiếng nổ do âm thanh phản xạ trên bức tường. Tốc độ âm thanh trong không khí là 330 m/s. Khoảng thời gian giữa hai tiếng nổ là:
Đáp án : D Phương pháp giải :
Sử dụng công thức \(S{\rm{ }} = {\rm{ }}v.t\) Lời giải chi tiết :
Khoảng cách giữa người và súng là: L = 165 – 30 = 135 m Gọi \({t_1}\) là thời gian lúc súng bắt đầu nổ đến tai người: \({t_1} = \frac{{{S_1}}}{v} = \frac{{135}}{v}\) \({t_2}\) là thời gian do âm thanh phản xạ trên bức tường sau khi nghe tiếng nổ: \({t_2} = \frac{{{S_2}}}{v} = \frac{{30 + 165}}{v}\) Thời gian giữa hai lần tiếng nổ đến tai người là: \(\Delta t = {t_2} - {t_1} = \frac{{30 + 165}}{v} - \frac{{135}}{v} = \frac{{60}}{v} = \frac{{60}}{{330}} = \frac{2}{{11}}s\)
Câu 21 :
Thuật ngữ âm “trầm” , “bổng” chỉ đặc tính nào của âm dưới đây?
Đáp án : C Lời giải chi tiết :
Ta có độ cao phụ thuộc vào tần số của âm. Tần số lớn \( \to \) âm bổng Tần số nhỏ \( \to \) âm trầm
Câu 22 :
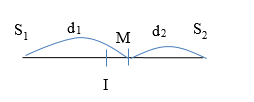
Ở bề mặt một chất lỏng có hai nguồn phát sóng kết hợp \({S_1}\) và \({S_2}\) cách nhau \(15cm\). Hai nguồn này dao động theo phương thẳng đứng có phương trình lần lượt là \({u_1} = 5cos50\pi t\left( {mm} \right)\) và \({u_2} = 5cos(50\pi t + \pi ){\rm{ }}\left( {mm} \right)\). Tốc độ truyền sóng trên mặt chất lỏng là \(120cm/s\). Xét các điểm trên \({S_1}{S_2}\). Gọi I là trung điểm của \({S_1}{S_2}\); M nằm cách I một đoạn 3cm sẽ dao động với biên độ:
Đáp án : D Phương pháp giải :
- Áp dụng công thức tính bước sóng: \(\lambda = \frac{v}{f}\) - Sử dụng công thức tính biên độ tại 1 điểm bất kì trong trường giao thoa với 2 nguồn ngược pha nhau: \(a = 2A\left| {c{\rm{os}}\left( {\pi \frac{{{d_1} - {d_2}}}{\lambda } + \frac{\pi }{2}} \right)} \right|\) Lời giải chi tiết :
Cách 1: + Bước sóng: \(\lambda = \frac{v}{f} = \frac{{120}}{{\frac{{50\pi }}{{2\pi }}}} = 4,8cm\) + Ta có biên độ dao động tại một điểm bất kì trong trường giao thoa: \(a = 2A\left| {c{\rm{os}}\left( {\pi \frac{{{d_1} - {d_2}}}{\lambda } + \frac{\pi }{2}} \right)} \right| = 10c{\rm{os}}\left( {\pi \frac{{{d_1} - {d_2}}}{\lambda } + \frac{\pi }{2}} \right)\)
Ta có: \({d_2} - {\rm{ }}{d_1} = {\rm{ }}2MI{\rm{ }} = {\rm{ }}6cm\) \( \to {a_M} = 10\left| {c{\rm{os}}\left( {\pi \frac{6}{{4,6}} + \frac{\pi }{2}} \right)} \right| = 10\left| {cos\left( {\frac{{7\pi }}{4}} \right)} \right| = 5\sqrt 2 mm\)
Câu 23 :
Sóng cơ truyền dọc theo trục Ox có phương trình \(u = 4cos(50πt – 0,125x) (mm)\). Tần số của sóng này bằng :
Đáp án : D Phương pháp giải :
+ Đọc phương trình li độ u + Sử dụng công thức liên hệ giữa tần số và tần số góc : \(\omega = 2\pi f \Rightarrow f = \dfrac{\omega }{{2\pi }}\) Lời giải chi tiết :
+ Từ phương trình li độ: \(u = 4cos(50πt – 0,125x) (mm)\) => Tần số góc \(\omega = 50\pi (rad/s)\) + Tần số của sóng này bằng : \(f = \dfrac{\omega }{{2\pi }} = \dfrac{{50\pi }}{{2\pi }} = 25Hz\)
Câu 24 :
Ở mặt nước, tại hai điểm A và B cách nhau \(19 cm\), có hai nguồn kết hợp dao động cùng pha theo phương thẳng đứng, phát ra hai sóng có bước sóng \(4 cm\). Trong vùng giao thoa, M là một điểm ở mặt nước thuộc đường trung trực của AB. Trên đoạn AM, số điểm cực tiểu giao thoa là
Đáp án : C Phương pháp giải :
Áp dụng điều kiện có cực tiểu giao thoa với hai nguồn cùng pha : \({d_1} - {d_2} = (2k + 1)\dfrac{\lambda }{2}\) Lời giải chi tiết :
Số điểm dao động với biên độ cực tiểu trên đoạn AM bằng số giá trị k thỏa mãn điều kiện \(\begin{array}{l}BM - AM \le {d_2} - {d_1} < AB \Leftrightarrow 0 \le \left( {k + \dfrac{1}{2}} \right)4 < 19\\ - 0,5 < k < 4,25 = > k = 0;1;2;3;4\end{array}\) Có 5 giá trị k thỏa mãn điều kiện.
Câu 25 :
Sóng dọc là sóng có phương dao động của các phần tử môi trường và phương truyền sóng hợp với nhau một góc
Đáp án : C Lời giải chi tiết :
Sóng dọc là sóng có phương dao động của các phần tử môi trường và phương truyền sóng hợp với nhau một góc \(0^0\) |




















Danh sách bình luận