Đề thi khảo sát chất lượng đầu năm lớp 12 môn Lí - Đề số 3Đề bài
Câu 1 :
Sự nhiễm điện của các vật do bao nhiêu nguyên nhân?
Câu 2 :
Lăng kính là:
Câu 3 :
Biểu thức nào sau đây xác định cảm ứng từ của dòng điện thẳng dài đặt trong không khí:
Câu 4 :
Một hạt proton chuyển động với vận tốc \(\overrightarrow v \) vào trong từ trường theo phương song song với đường sức từ thì:
Câu 5 :
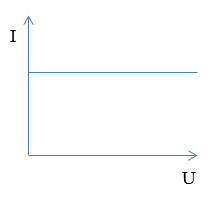
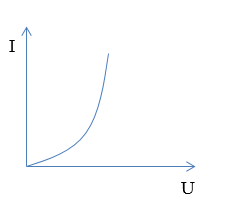
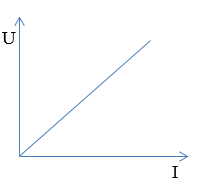
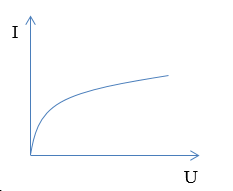
Đồ thị nào sau đây diễn tả đúng mối liên hệ giữa hiệu điện thế $(U)$ và cường độ dòng điện $(I)$ trong đoạn mạch chỉ có điện trở?
Câu 6 :
Chọn câu đúng
Câu 7 :
Phát biểu nào sau đây là đúng?
Câu 8 :
Một khung dây hình vuông cạnh 5cm đặt trong từ trường đều có cảm ứng từ B = 8.10-4T. Từ thông qua hình vuông đó bằng 10-6 Wb. Góc hợp bởi giữa véctơ cảm ứng từ và véctơ pháp tuyến của hình vuông đó là:
Câu 9 :
Từ phổ là:
Câu 10 :
Hiệu điện thế giữa hai điểm:
Câu 11 :
Phát biểu nào sau đây không đúng ?
Câu 12 :
Trong các ứng dụng sau đây, ứng dụng của hiện tượng phản xạ toàn phần là:
Câu 13 :
Năng lượng từ trường của ống dây được xác định bởi biểu thức:
Câu 14 :
Đáy của một cốc thủy tinh là một bản mặt song song chiết suất n = 1,5. Đặt cốc lên một trang sách rồi nhìn qua đáy cốc theo phương gần thẳng đứng thì thấy dòng chữ trên trang sách dường như nằm trong thủy tinh, cách mặt trong của đáy 0,6cm. Bề dày của đáy cốc là:
Câu 15 :
Tụ xoay có điện dung thay đổi từ \({C_1} = 30pF\) đến \({C_2} = 120pF\) khi góc xoay biến thiên từ 00 đến 900. Biết điện dung của tụ xoay là hàm bậc nhất của góc xoay . Biểu thức nào sau đây là đúng?
Câu 16 :
Khi tính số bội giác của kính thiên văn, góc \({\alpha _0}\) được chọn là:
Câu 17 :
Một thấu kính có dạng một mặt phẳng và một mặt cầu làm bằng thủy tinh có chiết suất n =1,5. Đặt trong không khí, một chùm sáng tới song song với trục chính cho chùm tia ló hội tụ tại điểm phía sau thấu kính, cách thấu kính 12cm. Bán kính của mặt cầu có giá trị là:
Câu 18 :
Một sợi dây bằng nhôm có điện trở \(135\Omega\) ở nhiệt độ 250C, điện trở của sợi dây đó ở 3000C là \(298\Omega\). Hệ số nhiệt điện trở của nhôm là:
Câu 19 :
Phát biểu nào sau đây đúng?
Câu 20 :
Hai dòng điện thẳng dài đặt song song cùng chiều, cách nhau \(d = 12cm\) trong không khí có \({I_2} = {I_1} = I = 10A\). Xác định cảm ứng từ tổng hợp tại điểm M cách đều \({I_1}\) và \({I_2}\) một khoảng x. Hãy xác định x để độ lớn cảm ứng từ tổng hợp do hai dòng điện gây ra đạt giá trị cực đại. Tính giá trị cực đại đó
Câu 21 :
Độ lớn của lực Lorenxơ được tính theo công thức:
Câu 22 :
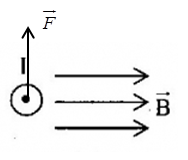
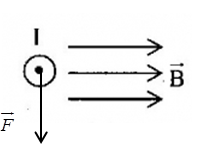
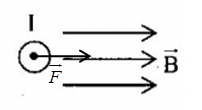
Một dây dẫn thẳng có dòng điện I đặt trong vùng không gian có từ trường đều như hình vẽ. 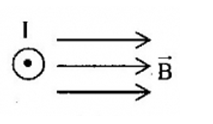 Xác định véctơ của đại lượng còn thiếu:
Câu 23 :
Một dây dẫn mang dòng điện \({I_1} = 5A\) đặt tại điểm A. Tại điểm B cách A \(5cm\) người ta đặt một dòng điện \({I_2}\) ngược chiều với \({I_1}\). Biết \({I_2} = 10A\), hãy xác định lực tương tác giữa chúng?
Câu 24 :
Mắt người và cá cùng cách mặt nước là \(40cm\), cùng nằm trên một mặt phẳng vuông góc với mặt nước. Biết chiết suất của nước là \(n = \dfrac{4}{3}\). Hỏi người thấy cá cách mình bao xa?
Câu 25 :
Phát biểu nào sau đây là đúng?
Câu 26 :
Môi trường nào dưới đây không chứa điện tích tự do?
Câu 27 :
Hai điện tích \({q_1} = - {2.10^{ - 8}}C\), \({q_2} = - 1,{8.10^{ - 7}}C\) đặt tại A và B trong không khí, \(AB = 8cm\). Một điện tích \({q_3}\) đặt tại C. Hỏi C ở đâu để \({q_3}\) cân bằng?
Câu 28 :
Tại ba đỉnh của tam giác đều \(ABC\), cạnh \(a = 10cm\) có ba điện tích điểm bằng nhau và bằng \(10nC\). Hãy xác định cường độ điện trường tại trung điểm của cạnh AB.
Câu 29 :
Một biến trở con chạy được làm bằng dây dẫn hợp kim Nikelin có điện trở suất \({4.10^{ - 7}}\Omega .m\), có tiết diện đầu là \(0,8m{m^2}\) và gồm \(300\) vòng cuốn quanh lõi sứ trụ tròn đường kính \(4,5cm\). Hiệu điện thế lớn nhất được phép đặt vào là \(63,585V\). Hỏi biến trở này chịu được dòng điện có cường độ lớn nhất là bao nhiêu?
Câu 30 :
Cho mạch điện như sau: 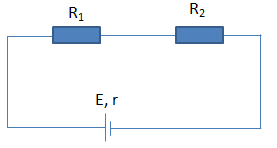 Biết \({R_1} = {R_2} = r\). Cường độ dòng điện chạy trong mạch là:
Lời giải và đáp án
Câu 1 :
Sự nhiễm điện của các vật do bao nhiêu nguyên nhân?
Đáp án : C Lời giải chi tiết :
Sự nhiễm điện của các vật do 3 nguyên nhân là: - Nhiễm điện do cọ xát - Nhiễm điện do tiếp xúc - Nhiễm điện do hưởng ứng
Câu 2 :
Lăng kính là:
Đáp án : C Lời giải chi tiết :
Lăng kính là một khối trong suốt, đồng nhất, được giới hạn bởi hai mặt phẳng không song song.
Câu 3 :
Biểu thức nào sau đây xác định cảm ứng từ của dòng điện thẳng dài đặt trong không khí:
Đáp án : B Lời giải chi tiết :
Cảm ứng từ của dòng điện thẳng dài đặt trong không khí được xác định bởi biểu thức: \(B = {2.10^{ - 7}}\frac{I}{r}\)
Câu 4 :
Một hạt proton chuyển động với vận tốc \(\overrightarrow v \) vào trong từ trường theo phương song song với đường sức từ thì:
Đáp án : C Lời giải chi tiết :
Ta có: proton chuyển động theo phương song song với đường sức từ => lực lorenxơ $f = 0$ => Hạt proton không chịu tác dụng của lực lorenxơ => vận tốc và hướng chuyển động của proton không thay đổi
Câu 5 :
Đồ thị nào sau đây diễn tả đúng mối liên hệ giữa hiệu điện thế $(U)$ và cường độ dòng điện $(I)$ trong đoạn mạch chỉ có điện trở?
Đáp án : C Phương pháp giải :
Vận dụng biểu thức định luật Ôm cho đoạn mạch chỉ có điện trở: \(I = \frac{U}{R}\) Lời giải chi tiết :
Ta có: Biểu thức định luật Ôm cho đoạn mạch chỉ có điện trở: \(I = \frac{U}{R} \to U = IR\) => Đồ thị có dạng của hàm số y = ax
Câu 6 :
Chọn câu đúng
Đáp án : D Lời giải chi tiết :
A, B, C - đúng
Câu 7 :
Phát biểu nào sau đây là đúng?
Đáp án : C Phương pháp giải :
Vận dụng lí thuyết về hiện tượng cảm ứng điện từ Lời giải chi tiết :
Vận dụng lí thuyết về hiện tượng cảm ứng điện từ ta suy ra: Một thanh dây dẫn chuyển động cắt các đường sức từ của một từ trường đều sao cho thanh luôn vuông góc với đường sức điện thì trong thanh xuất hiện một điện trường cảm ứng
Câu 8 :
Một khung dây hình vuông cạnh 5cm đặt trong từ trường đều có cảm ứng từ B = 8.10-4T. Từ thông qua hình vuông đó bằng 10-6 Wb. Góc hợp bởi giữa véctơ cảm ứng từ và véctơ pháp tuyến của hình vuông đó là:
Đáp án : D Phương pháp giải :
+ Áp dụng công thức tính diện tích hình vuông: \(S = {a^2}\) + Vận dụng biểu thức tính từ thông qua diện tích S: \(\Phi = BSc{\rm{os}}\alpha \) Lời giải chi tiết :
Ta có: + Diện tích của khung: \(S = {a^2} = 0,{05^2} = 2,{5.10^{ - 3}}({m^2})\) + Từ thông qua khung: \(\Phi = BSc{\rm{os}}\alpha \to c{\rm{os}}\alpha {\rm{ = }}\frac{\Phi }{{BS}} = \frac{{{{10}^{ - 6}}}}{{{{8.10}^{ - 4}}.2,{{5.10}^{ - 3}}}} = 0,5 \to \alpha = {60^0}\)
Câu 9 :
Từ phổ là:
Đáp án : A Lời giải chi tiết :
- Từ phổ: + Dùng mạt sắt rắc đều lên một tấm kính đặt trên nam châm, gõ nhẹ tấm kính ta nhận được từ phổ của nam châm. + Hình ảnh của các đường mạt sắt cho ta hình ảnh của các đường sức từ của từ trường
Câu 10 :
Hiệu điện thế giữa hai điểm:
Đáp án : A Lời giải chi tiết :
Hiệu điện thế giữa hai điểm đặc trưng cho khả năng sinh công của điện trường trong sự di chuyển của điện tích q từ điểm nọ đến điểm kia
Câu 11 :
Phát biểu nào sau đây không đúng ?
Đáp án : A Phương pháp giải :
+ Sử dụng định nghĩa về dòng điện cảm ứng + Sử dụng công thức tính từ thông qua một diện tích S: Lời giải chi tiết :
Ta có: + Dòng điện xuất hiện khi có sự biến đổi từ thông qua mạch điện kín gọi là dòng điện cảm ứng + từ thông qua một diện tích S: A- sai vì khi khung quay quanh trục song song với các đường cảm ứng từ thì từ thông qua khung dây luôn bằng 0 => không có dòng điện cảm ứng B, C, D - đúng
Câu 12 :
Trong các ứng dụng sau đây, ứng dụng của hiện tượng phản xạ toàn phần là:
Đáp án : D Lời giải chi tiết :
Hiện tượng phản xạ toàn phần được ứng dụng làm cáp quang để để truyền tín hiệu trong thông tin và để nội soi trong y học
Câu 13 :
Năng lượng từ trường của ống dây được xác định bởi biểu thức:
Đáp án : B Lời giải chi tiết :
Năng lượng từ trường của ống dây được xác định bởi biểu thức: \({\rm{W}} = \frac{{L{i^2}}}{2}\)
Câu 14 :
Đáy của một cốc thủy tinh là một bản mặt song song chiết suất n = 1,5. Đặt cốc lên một trang sách rồi nhìn qua đáy cốc theo phương gần thẳng đứng thì thấy dòng chữ trên trang sách dường như nằm trong thủy tinh, cách mặt trong của đáy 0,6cm. Bề dày của đáy cốc là:
Đáp án : B Phương pháp giải :
Vẽ ảnh của tia sáng qua bản mặt song song Lời giải chi tiết :
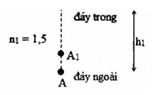 Coi đáy cốc thủy tinh là một bản mặt song song có độ dày là h1, ảnh của điểm A qua bản mặt song song thủy tinh là A1. Độ dịch chuyển ảnh A1 so với A là: \(A{A_1} = {h_1}\left( {1 - \frac{1}{n}} \right) = {h_1}\left( {1 - \frac{1}{{1,5}}} \right) = \frac{{h{}_1}}{3}\) Theo đề bài, ta có: ảnh A1 cách đáy trong đoạn 0,6cm \( \to A{A_1} = {h_1} - 0,6 \leftrightarrow \frac{{{h_1}}}{3} = {h_1} - 0,6 \to {h_1} = 0,9cm\)
Câu 15 :
Tụ xoay có điện dung thay đổi từ \({C_1} = 30pF\) đến \({C_2} = 120pF\) khi góc xoay biến thiên từ 00 đến 900. Biết điện dung của tụ xoay là hàm bậc nhất của góc xoay . Biểu thức nào sau đây là đúng?
Đáp án : A Lời giải chi tiết :
+ Vì điện dung của tụ là hàm bậc nhất của góc xoay nên ta có: \(C = \alpha a + b\) (a, b là hằng số) + Khi \(\alpha = 0\) thì \({C_1} = 30pF\) và khi \(\alpha = {90^0}\) thì \({C_2} = 120pF\) nên, ta có: \(\left\{ \begin{array}{l}30 = 0{\rm{a}} + b\\120 = 90{\rm{a}} + b\end{array} \right. \to \left\{ \begin{array}{l}a = 1\\b = 30\end{array} \right.\) => Biểu thức của điện dung: \(C = \alpha + 30{\rm{ }}(pF)\)
Câu 16 :
Khi tính số bội giác của kính thiên văn, góc \({\alpha _0}\) được chọn là:
Đáp án : D Lời giải chi tiết :
\({\alpha _0} = \tan {\alpha _0} = \frac{{{A_1}{B_1}}}{{{f_1}}}\): góc trông trực tiếp vật
Câu 17 :
Một thấu kính có dạng một mặt phẳng và một mặt cầu làm bằng thủy tinh có chiết suất n =1,5. Đặt trong không khí, một chùm sáng tới song song với trục chính cho chùm tia ló hội tụ tại điểm phía sau thấu kính, cách thấu kính 12cm. Bán kính của mặt cầu có giá trị là:
Đáp án : D Phương pháp giải :
+ Sử dụng tính chất của các chùm tia xác định loại thấu kính + Sử dụng công thức: \(\frac{1}{f} = \left( {n - 1} \right)\left( {\frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}} \right)\) Lời giải chi tiết :
+ Vì chùm tia ló hội tụ nên đó là thấu kính hội tụ => mặt cầu là mặt lồi + Ta có: \(f = 12cm\) theo đề bài Lại có: \(\frac{1}{f} = \left( {n - 1} \right)\left( {\frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}} \right)\) \( \to \frac{1}{{12}} = \left( {1,5 - 1} \right)\left( {\frac{1}{{{R_1}}} + \frac{1}{\infty }} \right) \to {R_1} = 6cm\)
Câu 18 :
Một sợi dây bằng nhôm có điện trở \(135\Omega\) ở nhiệt độ 250C, điện trở của sợi dây đó ở 3000C là \(298\Omega\). Hệ số nhiệt điện trở của nhôm là:
Đáp án : B Phương pháp giải :
Áp dụng biểu thức \(R = {R_0}\left( {1 + \alpha \Delta t} \right)\) Lời giải chi tiết :
Ta có: \(R = {R_0}\left( {1 + \alpha \Delta t} \right)\), + \({R_1} = 135\Omega \) ở \({t_1} = {25^0}C\) + \({R_2} = 298\Omega \) ở \({t_2} = {300^0}C\) Mặt khác, ta có: \({R_2} = {R_1}\left( {1 + \alpha \left( {{t_2} - {t_1}} \right)} \right)\) \(\begin{array}{l} \leftrightarrow 298 = 135\left( {1 + \alpha \left( {300 - 25} \right)} \right)\\ \to \alpha = {4,4.10^{ - 3}}{K^{ - 1}}\end{array}\)
Câu 19 :
Phát biểu nào sau đây đúng?
Đáp án : C Lời giải chi tiết :
A – sai vì: Qua bất kỳ điểm nào trong từ trường ta cũng có thể vẽ được một đường sức từ. B – sai vì: Đường sức từ do nam châm thẳng tạo ra xung quanh nó là những đường cong kín C – đúng D – sai vì: Đường sức từ trong từ trường đều là những đường thẳng song song cách đều nhau
Câu 20 :
Hai dòng điện thẳng dài đặt song song cùng chiều, cách nhau \(d = 12cm\) trong không khí có \({I_2} = {I_1} = I = 10A\). Xác định cảm ứng từ tổng hợp tại điểm M cách đều \({I_1}\) và \({I_2}\) một khoảng x. Hãy xác định x để độ lớn cảm ứng từ tổng hợp do hai dòng điện gây ra đạt giá trị cực đại. Tính giá trị cực đại đó
Đáp án : A Phương pháp giải :
+ Áp dụng các bước giải xác định cảm ứng từ (Xem lí thuyết phần V) + Áp dụng biểu thức xác định cảm ứng từ của dòng điện thẳng: \(B = {2.10^{ - 7}}\dfrac{I}{r}\) + Áp dụng BĐT Côsi Lời giải chi tiết :
Giả sử hai dây dẫn được đặt vuông góc với mặt phẵng hình vẽ, dòng \({I_1}\) đi vào tại A, dòng \({I_2}\) đi vào tại B. Các dòng điện \({I_1}\) và \({I_2}\) gây ra tại M các véc tơ cảm ứng từ \(\mathop {{B_1}}\limits^ \to \) và \(\mathop {{B_2}}\limits^ \to \) có phương chiều như hình vẽ: 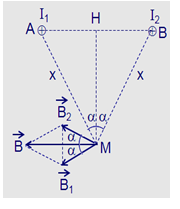 Có độ lớn: \({B_1} = {B_2} = {2.10^{ - 7}}\dfrac{I}{x}\) Từ hình ta có: \(\left\{ \begin{array}{l}AH = \dfrac{{12}}{2} = 6cm = 0,06m\\HM = \sqrt {A{M^2} - A{H^2}} = \sqrt {{x^2} - 0,{{06}^2}} \\cos\alpha = \dfrac{{HM}}{{AM}}\end{array} \right.\) Cảm ứng từ tổng hợp tại M là: \(\mathop B\limits^ \to = \mathop {{B_1}}\limits^ \to + \mathop {{B_2}}\limits^ \to \) có phương chiều như hình vẽ và có độ lớn: \(\begin{array}{l}B = 2{B_1}cos\alpha = {2.2.10^{ - 7}}\dfrac{I}{x}\dfrac{{HM}}{{AM}}\\ = {4.10^{ - 7}}.\dfrac{{10}}{x}\dfrac{{\sqrt {{x^2} - 0,{{06}^2}} }}{x}\\ = {4.10^{ - 6}}\dfrac{{\sqrt {{x^2} - 0,{{06}^2}} }}{{{x^2}}}\end{array}\) Nhận thấy, B đạt cực đại khi \(\dfrac{{\sqrt {{x^2} - 0,{{06}^2}} }}{{{x^2}}}\) đạt cực đại: Ta có: \(\begin{array}{l}\dfrac{{\sqrt {{x^2} - 0,{{06}^2}} }}{{{x^2}}} = \sqrt {\dfrac{{{x^2} - 0,{{06}^2}}}{{{x^4}}}} = \sqrt {\dfrac{1}{{{x^2}}}\left( {1 - \dfrac{{0,{{06}^2}}}{{{x^2}}}} \right)} \\ = \sqrt {\dfrac{1}{{0,{{06}^2}}}\dfrac{{0,{{06}^2}}}{{{x^2}}}\left( {1 - \dfrac{{0,{{06}^2}}}{{{x^2}}}} \right)} = \dfrac{1}{{0,06}}\sqrt {\dfrac{{0,{{06}^2}}}{{{x^2}}}\left( {1 - \dfrac{{0,{{06}^2}}}{{{x^2}}}} \right)} \end{array}\) Do \(d < x \to 1 - \dfrac{{0,{{06}^2}}}{{{{\rm{x}}^2}}} > 0\) Áp dụng BĐT cosi (\(\sqrt {ab} \le \dfrac{{a + b}}{2}\) ) ta có: \(\sqrt {\dfrac{{0,{{06}^2}}}{{{x^2}}}\left( {1 - \dfrac{{0,{{06}^2}}}{{{x^2}}}} \right)} \le \dfrac{{\dfrac{{0,{{06}^2}}}{{{x^2}}} + 1 - \dfrac{{0,{{06}^2}}}{{{x^2}}}}}{2} = \dfrac{1}{2}\) Dấu “ = ” xảy ra khi: \(\dfrac{{0,{{06}^2}}}{{{x^2}}} = 1 - \dfrac{{0,{{06}^2}}}{{{x^2}}} \Rightarrow x = 6\sqrt 2 {.10^{ - 2}}m\) Khi đó \({B_{max}} = {4.10^{ - 6}}\dfrac{1}{{0,06}}.\dfrac{1}{2} = 3,{33.10^{ - 5}}T\)
Câu 21 :
Độ lớn của lực Lorenxơ được tính theo công thức:
Đáp án : B Lời giải chi tiết :
Độ lớn của lực Lorenxơ được xác định bởi biểu thức: \(f = \left| q \right|vB\sin \alpha \)
Câu 22 :
Một dây dẫn thẳng có dòng điện I đặt trong vùng không gian có từ trường đều như hình vẽ.  Xác định véctơ của đại lượng còn thiếu:
Đáp án : A Phương pháp giải :
Vận dụng quy tăc bàn tay trái: Đặt bàn tay trái sao cho các đường sức từ đâm xuyên vào lòng bàn tay, dòng điện chạy từ cổ tay đến ngón tay, thì ngón cái choãi ra là chiều của lực từ tác dụng lên dòng điện Lời giải chi tiết :
Quy tắc bàn tay trái: Đặt bàn tay trái sao cho các đường sức từ đâm xuyên vào lòng bàn tay, dòng điện chạy từ cổ tay đến ngón tay, thì ngón cái choãi ra là chiều của lực từ tác dụng lên dòng điện Ta suy ra: 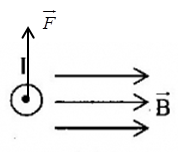
Câu 23 :
Một dây dẫn mang dòng điện \({I_1} = 5A\) đặt tại điểm A. Tại điểm B cách A \(5cm\) người ta đặt một dòng điện \({I_2}\) ngược chiều với \({I_1}\). Biết \({I_2} = 10A\), hãy xác định lực tương tác giữa chúng?
Đáp án : B Phương pháp giải :
Vận dụng biểu thức xác định lực từ tác dụng lên mỗi đơn vị chiều dài dây: \(F = {2.10^{ - 7}}\dfrac{{{I_1}{I_2}}}{r}\) Lời giải chi tiết :
Ta có, 2 dòng I1 và I2 ngược chiều nhau => lực tương tác là lực đẩy \(F = {2.10^{ - 7}}\dfrac{{{I_1}{I_2}}}{r} = {2.10^{ - 7}}\dfrac{{5.10}}{{0,05}} = {2.10^{ - 4}}N\)
Câu 24 :
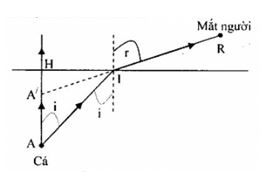
Mắt người và cá cùng cách mặt nước là \(40cm\), cùng nằm trên một mặt phẳng vuông góc với mặt nước. Biết chiết suất của nước là \(n = \dfrac{4}{3}\). Hỏi người thấy cá cách mình bao xa?
Đáp án : B Phương pháp giải :
+ Vẽ đường truyền tia sáng qua lưỡng chất phẳng + Sử dụng hệ thức lượng trong tam giác + Vận dụng biểu thức định luật khúc xạ ánh sáng: \({n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}}\) Lời giải chi tiết :
Khi người nhìn thấy cá thì tia sáng từ cá đến mắt người (hình vẽ) + Vì mắt nhìn xuống đáy chậu gần vuông góc nên góc r rất nhỏ => i cũng rất nhỏ + Gọi A là cá thật và A’ là ảnh của cá
Từ hình vẽ, ta có: \(\left\{ \begin{array}{l}\tan i = \dfrac{{HI}}{{HA}} \approx \sin i \approx i\\{\mathop{\rm t}\nolimits} {\rm{anr}} = \dfrac{{HI}}{{HA'}} \approx {\mathop{\rm s}\nolimits} {\rm{inr}} \approx {\rm{r}}\end{array} \right.\) Theo định luật khúc xạ ánh sáng, ta có: \(n\sin i = {\mathop{\rm s}\nolimits} {\rm{inr}} \to \dfrac{{\sin i}}{{{\mathop{\rm s}\nolimits} {\rm{inr}}}} = \dfrac{1}{n} \leftrightarrow \dfrac{{HA'}}{{HA}} = \dfrac{1}{n} \to HA' = \dfrac{{HA}}{n} = \dfrac{{40}}{{\dfrac{4}{3}}} = 30cm\) => Người nhìn thấy cá cách mắt mình đoạn 40 + 30 = 70cm
Câu 25 :
Phát biểu nào sau đây là đúng?
Đáp án : C Lời giải chi tiết :
A – sai vì: phản xạ toàn phần xảy ra khi tia sáng đi từ môi trường có chiết suất lớn sang môi trường có chiết suất nhỏ hơn. B – sai vì: khi truyền ánh sáng từ môi trường có chiết suất lướn sang môi trường chiết suất nhỏ hơn có thể xảy ra hiện tượng phản xạ toàn phần => không phải luôn có tia khúc xạ C - đúng D – sai vì: Khi có sự phản xạ toàn phần, cường độ sáng của chùm phản xạ gần như bằng cường độ sáng của chùm sáng tới.
Câu 26 :
Môi trường nào dưới đây không chứa điện tích tự do?
Đáp án : D Lời giải chi tiết :
Trong môi trường nước cất không có các electron tự do
Câu 27 :
Hai điện tích \({q_1} = - {2.10^{ - 8}}C\), \({q_2} = - 1,{8.10^{ - 7}}C\) đặt tại A và B trong không khí, \(AB = 8cm\). Một điện tích \({q_3}\) đặt tại C. Hỏi C ở đâu để \({q_3}\) cân bằng?
Đáp án : C Phương pháp giải :
+ Áp dụng biểu thức định luật Cu-lông: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\) + Vận dụng phương pháp tổng hợp lực + Vận dụng điều kiện cân bằng của vật Lời giải chi tiết :
Gọi \(\overrightarrow {{F_{13}}} ,\overrightarrow {{F_{23}}} \) lần lượt là lực do \({q_1},{q_2}\) tác dụng lên \({q_3}\) + Điều kiện cân bằng của \({q_3}\): \(\overrightarrow {{F_{12}}} + \overrightarrow {{F_{23}}} = \overrightarrow 0 \) \( \Rightarrow \overrightarrow {{F_{13}}} = - \overrightarrow {{F_{23}}} \) \( \Rightarrow \) điểm C phải thuộc AB + Vì \({q_1}\) và \({q_2}\) cùng dấu nên ta suy ra C phải nằm trong AB + Lại có \({F_{13}} = {F_{23}}\) \(\begin{array}{l} \Leftrightarrow k\dfrac{{\left| {{q_1}{q_3}} \right|}}{{C{A^2}}} = k\dfrac{{\left| {{q_2}{q_3}} \right|}}{{C{B^2}}}\\ \Rightarrow \dfrac{{{q_1}}}{{C{A^2}}} = \dfrac{{{q_2}}}{{C{B^2}}}\\ \Rightarrow \dfrac{{CB}}{{CA}} = \sqrt {\dfrac{{{q_2}}}{{{q_1}}}} = \sqrt {\dfrac{{ - 1,{{8.10}^{ - 7}}}}{{ - {{2.10}^{ - 8}}}}} = 3\end{array}\) \( \Rightarrow CB = 3CA\) (1) \( \Rightarrow \) C gần A hơn + Mặt khác, ta có: \(CA + CB = 8cm\) (2) Từ (1) và (2) ta suy ra: \(\left\{ \begin{array}{l}CA = 2cm\\CB = 6cm\end{array} \right.\)
Câu 28 :
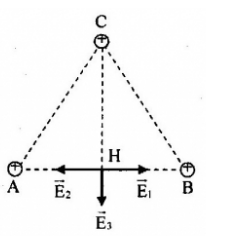
Tại ba đỉnh của tam giác đều \(ABC\), cạnh \(a = 10cm\) có ba điện tích điểm bằng nhau và bằng \(10nC\). Hãy xác định cường độ điện trường tại trung điểm của cạnh AB.
Đáp án : A Phương pháp giải :
+ Áp dụng nguyên lí chồng chất điện trường: \(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \) + Áp dụng biểu thức xác định cường độ điện trường: \(E = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\) Lời giải chi tiết :
Gọi \(H\) - trung điểm của cạnh \(AB\) Gọi \(\overrightarrow {{E_1}} ,\overrightarrow {{E_2}} ,\overrightarrow {{E_3}} \) lần lượt là cường độ điện trường do điện tích \({q_1},{q_2},{q_3}\) gây ra tại \(H\) Ta có, các véc-tơ \(\overrightarrow {{E_1}} ,\overrightarrow {{E_2}} ,\overrightarrow {{E_3}} \) được biểu diễn như hình
Ta có: \({E_1} = {E_2} = k\dfrac{{\left| q \right|}}{{{{\left( {\dfrac{{AB}}{2}} \right)}^2}}}\) \({E_3} = k\dfrac{{\left| q \right|}}{{C{H^2}}}\) Lại có: \(\begin{array}{l}CH = \sqrt {C{B^2} - B{H^2}} = \sqrt {C{B^2} - {{\left( {\dfrac{{AB}}{2}} \right)}^2}} \\ = \sqrt {{{10}^2} - \dfrac{{{{10}^2}}}{4}} = 5\sqrt 3 cm\end{array}\) Ta suy ra: \({E_3} = {9.10^9}\dfrac{{{{10.10}^{ - 9}}}}{{{{\left( {5\sqrt 3 {{.10}^{ - 2}}} \right)}^2}}} = 12000V/m\) Ta có, cường độ điện trường tổng hợp tại \(H\): \(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + \overrightarrow {{E_3}} \) Vì \(\left\{ \begin{array}{l}\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \\{E_1} = {E_2}\end{array} \right. \Rightarrow \overrightarrow {{E_{12}}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} = \overrightarrow 0 \) Ta suy ra: \(\overrightarrow E = \overrightarrow {{E_3}} \) \( \Rightarrow E = {E_3} = 12000V/m\)
Câu 29 :
Một biến trở con chạy được làm bằng dây dẫn hợp kim Nikelin có điện trở suất \({4.10^{ - 7}}\Omega .m\), có tiết diện đầu là \(0,8m{m^2}\) và gồm \(300\) vòng cuốn quanh lõi sứ trụ tròn đường kính \(4,5cm\). Hiệu điện thế lớn nhất được phép đặt vào là \(63,585V\). Hỏi biến trở này chịu được dòng điện có cường độ lớn nhất là bao nhiêu?
Đáp án : A Phương pháp giải :
+ Sử dụng biểu thức tính chu vi vòng tròn: \(C = 2\pi R = \pi d\) + Sử dụng biểu thức tính điện trở: \(R = \rho \dfrac{l}{S}\) + Sử dụng biểu thức định luật ôm: \(I = \dfrac{U}{R}\) Lời giải chi tiết :
Ta có: + Chiều dài của một vòng quấn là: \(C = 2\pi R = \pi d = 2\pi .0,045 = 0,1414m\) + Chiều dài của toàn bộ dây quấn: \(l = nC = 300.0,1414 = 42,42m\) + Điện trở lớn nhất của biến trở là: \(R = \rho \dfrac{l}{S} = {4.10^{ - 7}}\dfrac{{42,42}}{{{{0,8.10}^{ - 6}}}} = 21,21\Omega \) Ta suy ra, dòng điện lớn nhất mà biến trở chịu được là: \({I_{max}} = \dfrac{{{U_{max}}}}{{{R_{max}}}} = \dfrac{{63,585}}{{21,21}} \approx 3A\)
Câu 30 :
Cho mạch điện như sau:  Biết \({R_1} = {R_2} = r\). Cường độ dòng điện chạy trong mạch là:
Đáp án : B Phương pháp giải :
Áp dụng định luật Ôm cho toàn mạch: \(I = \dfrac{E}{{R + r}}\) Lời giải chi tiết :
Ta có: \({R_1}nt{R_2}\) Suy ra điện trở tương đương của mạch ngoài: \(R = {R_1} + {R_2} = 2r\) Cường độ dòng điện trong mạch: \(I = \dfrac{E}{{R + r}} = \dfrac{E}{{2r + r}} = \dfrac{E}{{3r}}\) |














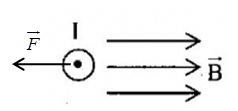






Danh sách bình luận