Đề kiểm tra 1 tiết chương 1: Dao động cơ - Đề số 01Đề bài
Câu 1 :
Biểu thức nào sau đây xác định cơ năng của con lắc lò xo dao động điều hòa?
Câu 2 :
Phương trình dao động điều hòa của một chất điểm có dạng \(x = {\rm{ }}Acos\left( a \right)t\) .Độ dài quỹ đạo của dao động là:
Câu 3 :
Trong con lắc lò xo nếu ta tăng khối lượng vật nặng lên \(4\) lần và độ cứng tăng \(2\) lần thì tần số dao động của vật:
Câu 4 :
Cho hai dao động điều hòa cùng phương, cùng tần số, lệch pha nhau một góc π/2 với biên độ A1 và A2. Dao động tổng hợp của hai dao động trên có biên độ là:
Câu 5 :
Phát biểu nào sau đây là sai khi nói về biên độ của dao động tổng hợp của hai dao động điều hoà cùng phương cùng tần số ?
Câu 6 :
Một đồng hồ quả lắc chạy đúng giờ tại Hà Nội (T = 2s). Ở nhiệt độ trung bình bằng 200C gồm vật nặng m và thanh treo mảnh, nhẹ bằng kim loại có hệ số nở dài \(\alpha = {2.10^{ - 5}}{K^{ - 1}}\). Đưa đồng hồ vào TP. Hồ Chí Minh có nhiệt độ trung bình 300C thì đồng hồ chạy nhanh hay chậm so với Hà Nội mỗi ngày bao nhiêu giây. Biết gia tốc trọng trường ở Hà Nội (g = 9,787 m/s2) ở TP.HCM (g = 9,793m/s2)
Câu 7 :
Một con lắc đơn dao động điều hòa với phương trình li độ dài: \(s = 2cos7t (cm)\) (t: giây), tại nơi có gia tốc trọng trường \(g = 9,8 (m/s^2)\). Tỷ số giữa lực căng dây và trọng lực tác dụng lên quả cầu ở vị trí cân bằng là:
Câu 8 :
Một con lắc đơn gồm một quả cầu kim loại nhỏ, khối lương m = 1 g, tích điện dương q = 5,66.10-7 C, được treo vào một sợi dây mảnh dài ℓ = 1,4 m trong điện trường đều có phương ngang, E = 104 V/m, tại một nơi có gia tốc trọng trường g = 9,79 m/s2. Ở VTCB, phương của dây treo hợp với phương thẳng đứng một góc
Câu 9 :
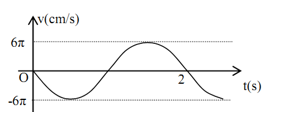 Đồ thị vận tốc của một vật cho ở hình bên, phương trình nào dưới đây là phương trình dao động của vật:
Câu 10 :
Một lò xo có độ cứng k treo thẳng đứng vào điểm cố định, đầu dưới có vật $m = 100 (g)$. Vật dao động điều hòa với tần số $f = 5 Hz$, cơ năng là $W=0,08J$ . Lấy $g = 10 m/s^2$, \({\pi ^2} = 10\). Tỉ số động năng và thế năng tại li độ $x = 2 cm$ là:
Câu 11 :
Treo một vật có khối lượng m1 vào con lắc lò xo có độ cứng k thì nó dao động với chu kì T1. Nếu treo quả nặng có khối lượng m2 vào lò xo trên thì nó dao động với chu kì T2. Khi treo cả hai vật vào lò xo thì chúng sẽ dao động với chu kì
Câu 12 :
Một vật có khối lượng không đổi, thực hiện đồng thời hai dao động điều hòa có phương trình dao động lần lượt là \({x_1} = {\rm{ }}10cos\left( {2pt{\rm{ }} + {\rm{ }}\varphi } \right)\) cm và \({x_2} = {A_2}cos(2\pi t - \dfrac{\pi }{2})cm\) thì dao động tổng hợp là \(x = Acos(2\pi t - \dfrac{\pi }{3})cm\). Khi năng lượng dao động của vật cực đại thì biên độ dao động A2 có giá trị là
Câu 13 :
Một vật dao động điều hòa có phương trình \(x = 5cos(2\pi t)\). Vận tốc của vật khi có li độ $x=3 cm$ là:
Câu 14 :
Chọn phát biểu sai trong các phương án sau:
Câu 15 :
Trạng thái của dao động gồm yếu tố nào?
Câu 16 :
Một vật dao động điều hoà với phương trình \(x = 4cos\left( {4\pi t + \dfrac{\pi }{6}} \right)cm\). Tìm số lần vật qua vị trí có gia tốc là \(32{\pi ^2}\left( {cm/{s^2}} \right)\) theo chiều âm trong thời gian \(5,75s\) tính từ thời điểm gốc.
Câu 17 :
Một vật dao động điều hòa theo phương trình \(x = Acos\left( {\omega t} \right)\). Phát biểu nào sau đây sai khi nói về chuyển động của vật?
Câu 18 :
Tại một nơi xác định, hai con lắc đơn có độ dài \({l_1}\) và \({l_2}\), dao động điều hoà với chu kì tương ứng \({T_1}\) và \({T_2}\). Tỉ số \(\dfrac{{{T_1}}}{{{T_2}}}\) bằng:
Câu 19 :
Hai con lắc lò xo nằm ngang dao động điều hòa dọc theo hai đường thẳng song song kề nhau và song song với trục Ox. Hai vật nặng có cùng khối lượng. Vị trí cân bằng của hai dao động đều nằm trên một đường thẳng qua gốc tọa độ và vuông góc với trục Ox. Đồ thị (1), (2) lần lượt biểu diễn mối liên hệ giữa lực kéo về Fkv và li độ x của con lắc 1 và con lắc 2. Biết tại thời điểm t, hai con lắc cùng qua vị trí cân bằng theo cùng một chiều. Sau đó một khoảng thời gian ngắn nhất bằng 0,5s con lắc 1 có động năng bằng một nửa cơ năng của nó, thì thế năng của con lắc 2 khi đó có giá trị gần nhất với giá trị nào sau đây?
Câu 20 :
Chọn phát biểu đúng về tần số của hệ dao động tự do?
Câu 21 :
Một con lắc lò xo đang dao động tắt dần, cơ năng ban đầu của nó là \(6J\). Sau bốn chu kì kể từ lúc bắt đầu dao động thì biên độ của nó giảm đi \(24\% \). Phần cơ năng của con lắc chuyển hóa thành nhiệt năng tính trung bình trong mỗi chu kì dao động của nó là:
Câu 22 :
Chọn phát biểu đúng về sự biến đổi năng lượng của một chất điểm dao động điều hòa với chu kỳ \(T\), tần số \(f\)?
Câu 23 :
Một con lắc lò xo treo thẳng đứng lò xo có độ cứng \(k = 120N/m\), vật dao động có khối lượng \(m = 300g\), lấy gia tốc trọng trường \(g = {\pi ^2} = 10m/{s^2}\). Từ vị trí cân bằng kéo vật xuống một đoạn \(3cm\) rồi truyền cho vật vận tốc đầu \(80cm/s\) hướng thẳng đứng thì vật dao động điều hòa. Thời gian lò xo bị nén trong một chu kỳ là:
Câu 24 :
Tiến hành thí nghiệm do gia tốc trọng trường bằng con lắc đơn, một học sinh đo được chiều dài con lắc là \((119 \pm 1)\) (cm). Chu kì dao động nhỏ của nó là \((2,20 \pm 0,01)\) (s). Lấy \({\pi ^2} = 9,87\) và bỏ qua sai số của số π. Gia tốc trọng trường do học sinh đo được tại nơi làm thí nghiệm là:
Câu 25 :
Khi nói về dao động cơ tắt dần, phát biểu nào sau đây sai?
Lời giải và đáp án
Câu 1 :
Biểu thức nào sau đây xác định cơ năng của con lắc lò xo dao động điều hòa?
Đáp án : D Lời giải chi tiết :
Cơ năng của con lắc lò xo dao động điều hòa: \(W = \dfrac{1}{2}k{A^2}\)
Câu 2 :
Phương trình dao động điều hòa của một chất điểm có dạng \(x = {\rm{ }}Acos\left( a \right)t\) .Độ dài quỹ đạo của dao động là:
Đáp án : B Phương pháp giải :
Đồng bộ hóa với phương trình dao động điều hòa và sử dụng công thức xác định quỹ đạo của vật trong dao động điều hòa. $x = A\cos \left( {\omega t + \varphi } \right)$ Lời giải chi tiết :
Ta có: + \(x = Acos\left( a \right)t\) + Độ dài quỹ đạo của dao động là: \(L = 2A\)
Câu 3 :
Trong con lắc lò xo nếu ta tăng khối lượng vật nặng lên \(4\) lần và độ cứng tăng \(2\) lần thì tần số dao động của vật:
Đáp án : D Phương pháp giải :
Vận dụng biểu thức xác định tần số dao động của con lắc lò xo: \(f = \dfrac{1}{{2\pi }}\sqrt {\dfrac{k}{m}} \) Lời giải chi tiết :
Ta có, tần số dao động của con lắc lò xo: \(f = \dfrac{1}{{2\pi }}\sqrt {\dfrac{k}{m}} \) Khi tăng khối lượng lên 4 lần và độ cứng tăng 2 lần tức là \(\left\{ \begin{array}{l}m' = 4m\\k' = 2k\end{array} \right.\) Tần số dao động của con lắc khi này: \(f' = \dfrac{1}{{2\pi }}\sqrt {\dfrac{{k'}}{{m'}}} = \dfrac{1}{{2\pi }}\sqrt {\dfrac{{2k}}{{4m}}} = \dfrac{1}{{2\pi }}\sqrt {\dfrac{k}{{2m}}} \) \(\dfrac{{f'}}{f} = \dfrac{{\dfrac{1}{{2\pi }}\sqrt {\dfrac{k}{{2m}}} }}{{\dfrac{1}{{2\pi }}\sqrt {\dfrac{k}{m}} }} = \dfrac{1}{{\sqrt 2 }}\) \( \Rightarrow f' = \dfrac{f}{{\sqrt 2 }}\) Hay nói cách khác khi tăng khối lượng lên $4$ lần và độ cứng tăng $2$ lần thì tần số dao động sẽ giảm \(\sqrt 2 \) lần
Câu 4 :
Cho hai dao động điều hòa cùng phương, cùng tần số, lệch pha nhau một góc π/2 với biên độ A1 và A2. Dao động tổng hợp của hai dao động trên có biên độ là:
Đáp án : B Phương pháp giải :
Sử dụng công thức tính biên độ dao động tổng hợp của hai dao động điều hoà cùng phương, cùng tần số: \(A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}\cos \Delta \varphi } \) Lời giải chi tiết :
Khi đó dao động tổng hợp được xác định bởi biểu thức \(\begin{array}{l}A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}\cos \Delta \varphi } ;\Delta \varphi = \frac{\pi }{2}\\ = > A = \sqrt {A_1^2 + A_2^2} \end{array}\)
Câu 5 :
Phát biểu nào sau đây là sai khi nói về biên độ của dao động tổng hợp của hai dao động điều hoà cùng phương cùng tần số ?
Đáp án : A Phương pháp giải :
Sử dụng công thức tính biên độ dao động tổng hợp của hai dao động điều hoà cùng phương, cùng tần số: \(A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}\cos \Delta \varphi } \) Lời giải chi tiết :
\(A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}{\rm{cos}}\Delta \varphi } \) Biên độ của dao động tổng hợp của hai dao động điều hoà cùng phương cùng tần số không phụ thuộc vào tần số của hai dao động thành phần.
Câu 6 :
Một đồng hồ quả lắc chạy đúng giờ tại Hà Nội (T = 2s). Ở nhiệt độ trung bình bằng 200C gồm vật nặng m và thanh treo mảnh, nhẹ bằng kim loại có hệ số nở dài \(\alpha = {2.10^{ - 5}}{K^{ - 1}}\). Đưa đồng hồ vào TP. Hồ Chí Minh có nhiệt độ trung bình 300C thì đồng hồ chạy nhanh hay chậm so với Hà Nội mỗi ngày bao nhiêu giây. Biết gia tốc trọng trường ở Hà Nội (g = 9,787 m/s2) ở TP.HCM (g = 9,793m/s2)
Đáp án : A Phương pháp giải :
Áp dụng công thức tính thời gian chạy sai của đồng hồ khi thay đổi nhiệt độ và vị trí trên trái đất: \(\frac{{\Delta T}}{T} = \frac{{{T_2} - {T_1}}}{{{T_1}}} = \frac{1}{2}\alpha \left( {{t_2} - {t_1}} \right) - \frac{1}{2}\frac{{\Delta g}}{{{g_1}}}\) Lời giải chi tiết :
Đưa đồng hồ từ Hà Nội vào thành phố HCM do nhiệt độ và gia tốc trọng trường g thay đổi nên đồng hồ sẽ chạy sai Áp dụng công thức tính thời gian chạy sai của đồng hồ trong 1s khi thay đổi nhiệt độ và vị trí trên trái đất: \(\frac{{\Delta T}}{T} = \frac{{{T_2} - {T_1}}}{{{T_1}}} = \frac{1}{2}\alpha \left( {{t_2} - {t_1}} \right) - \frac{1}{2}\frac{{\Delta g}}{{{g_1}}} = \frac{1}{2}{.2.10^{ - 5}}\left( {30 - 20} \right) - \frac{1}{2}\frac{{(9,793 - 9,787)}}{{9,787}} = - 2,{07.10^{ - 4}} < 0\) => Đồng hồ chạy nhanh Mỗi ngày, đồng hồ chạy nhanh khoảng thời gian: \(\theta = \left| {\frac{{\Delta T}}{T}} \right|.24.60.60 = 17,84{\rm{s}}\)
Câu 7 :
Một con lắc đơn dao động điều hòa với phương trình li độ dài: \(s = 2cos7t (cm)\) (t: giây), tại nơi có gia tốc trọng trường \(g = 9,8 (m/s^2)\). Tỷ số giữa lực căng dây và trọng lực tác dụng lên quả cầu ở vị trí cân bằng là:
Đáp án : C Phương pháp giải :
+ Đọc phương trình li độ dao động của con lắc đơn + Vận dụng biểu thức tính tần số góc dao động của con lắc đơn. + Áp dụng biểu thức xác định lực căng dây \(T = mg(3c{\rm{os}}\alpha - 2c{\rm{os}}{\alpha _0})\) Lời giải chi tiết :
Từ phương trình li độ dài của con lắc đơn: \(s = 2cos7t\) Ta có: Tần số góc của dao động: \(ω =7 (rad/s)\) Mặt khác: \(\omega = \sqrt {\dfrac{g}{l}} = 7 \to l = \dfrac{g}{{{\omega ^2}}} = \dfrac{{9,8}}{{{7^2}}} = 0,2m\) \(s_0= 2cm = 0,02m=l\alpha_0 \\\to \alpha_0= 0,1 rad = 5,73^0\) + Lực căng dây tại VTCB: \(T = mg(3 - 2c{\rm{os}}{\alpha _0}) \approx 1,01mg\) \( \to \dfrac{T}{P} = \dfrac{{1,01mg}}{{mg}} = 1,01\)
Câu 8 :
Một con lắc đơn gồm một quả cầu kim loại nhỏ, khối lương m = 1 g, tích điện dương q = 5,66.10-7 C, được treo vào một sợi dây mảnh dài ℓ = 1,4 m trong điện trường đều có phương ngang, E = 104 V/m, tại một nơi có gia tốc trọng trường g = 9,79 m/s2. Ở VTCB, phương của dây treo hợp với phương thẳng đứng một góc
Đáp án : A Phương pháp giải :
+ Áp dụng công thức tính lực điện Fđ = qE + Áp dụng bài toán con lắc đơn chịu thêm tác dụng của lực điện Lời giải chi tiết :
Ta có:\(\overrightarrow E \) có phương ngang =>\(\overrightarrow {{F_d}} \) có phương ngang Ta có: \(\tan \alpha = \frac{{{F_d}}}{P} = \frac{{qE}}{{mg}} = \frac{{5,{{66.10}^{ - 7}}{{.10}^4}}}{{{{10}^{ - 3}}.9,79}} = 0,5781 \to \alpha = {30^0}\) 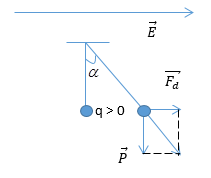
Câu 9 :
 Đồ thị vận tốc của một vật cho ở hình bên, phương trình nào dưới đây là phương trình dao động của vật:
Đáp án : B Phương pháp giải :
- Sử dụng phương pháp đọc đồ thị vận tốc theo thời gian của vật + Từ đồ thị xác định A, chu kì T, li độ và vận tốc tại thời điểm t = 0 Lời giải chi tiết :
Từ đồ thị, ta có: $T{\rm{ }} = {\rm{ }}2s \to \omega = \frac{{2\pi }}{T} = \pi ra{\rm{d}}/s$ $A\omega = 6\pi cm/s \to A = \frac{{6\pi }}{\omega } = \frac{{6\pi }}{\pi } = 6cm$ Tại t = 0: \({\rm{v = - A}}\omega {\rm{sin}}\varphi = 0 \to \sin \varphi = 0 \to \left[ \begin{array}{l}\varphi = 0\\\varphi = \pi \end{array} \right.\) và đang đi theo chiều âm\( \to \varphi = 0\) \( \Rightarrow x = 6c{\rm{os}}\left( {\pi t} \right)cm\)
Câu 10 :
Một lò xo có độ cứng k treo thẳng đứng vào điểm cố định, đầu dưới có vật $m = 100 (g)$. Vật dao động điều hòa với tần số $f = 5 Hz$, cơ năng là $W=0,08J$ . Lấy $g = 10 m/s^2$, \({\pi ^2} = 10\). Tỉ số động năng và thế năng tại li độ $x = 2 cm$ là:
Đáp án : A Phương pháp giải :
+ Áp dụng biểu thức xác định thế năng của con lắc lò xo: \({{\rm{W}}_t} = \dfrac{1}{2}k{{\rm{x}}^2}\) + Áp dụng biểu thức cơ năng: \({\text{W}} = {{\text{W}}_t} + {{\text{W}}_d}\) Lời giải chi tiết :
Tần số góc: \(\omega = 2\pi f = 10\pi (ra{\rm{d}}/s)\) Tại li độ $x = 2cm$ có: + Thế năng: \({{\rm{W}}_t} = \dfrac{1}{2}k{{\rm{x}}^2} = \dfrac{1}{2}m{\omega ^2}{x^2} = \dfrac{1}{2}0,1.{(10\pi )^2}{(0,02)^2} = 0,02J\) + Động năng: \({{\text{W}}_d} = {\text{W - }}{{\text{W}}_t} = 0,08 - 0,02 = 0,06J\) \(\dfrac{{{{\text{W}}_d}}}{{{{\text{W}}_t}}} = \dfrac{{0,06}}{{0,02}} = 3\)
Câu 11 :
Treo một vật có khối lượng m1 vào con lắc lò xo có độ cứng k thì nó dao động với chu kì T1. Nếu treo quả nặng có khối lượng m2 vào lò xo trên thì nó dao động với chu kì T2. Khi treo cả hai vật vào lò xo thì chúng sẽ dao động với chu kì
Đáp án : D Phương pháp giải :
Xem nội dung mục 3 - phần II : Sự thay đổi chu kì - tần số - tần số góc theo khối lượng vật nặng Lời giải chi tiết :
Ta có: \(T = 2\pi \sqrt {\frac{m}{k}} \to {T^2} \sim m\) => Khi treo cả hai vật vào lò xo thì chu kì dao động là: \(T = \sqrt {T_1^2 + T_2^2} \)
Câu 12 :
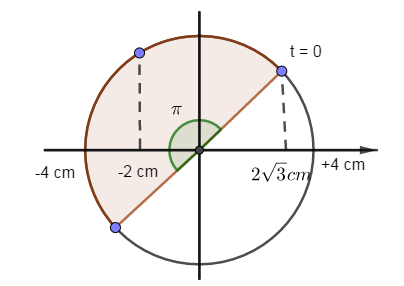
Một vật có khối lượng không đổi, thực hiện đồng thời hai dao động điều hòa có phương trình dao động lần lượt là \({x_1} = {\rm{ }}10cos\left( {2pt{\rm{ }} + {\rm{ }}\varphi } \right)\) cm và \({x_2} = {A_2}cos(2\pi t - \dfrac{\pi }{2})cm\) thì dao động tổng hợp là \(x = Acos(2\pi t - \dfrac{\pi }{3})cm\). Khi năng lượng dao động của vật cực đại thì biên độ dao động A2 có giá trị là
Đáp án : B Phương pháp giải :
Sử dụng giản đồ vectơ Lời giải chi tiết :
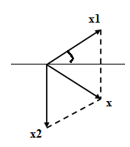 \(\begin{array}{l}\dfrac{{10}}{{\sin 30}} = \dfrac{{{A_2}}}{{\sin (60 + \varphi )}} = \dfrac{A}{{\sin (90 - \varphi )}}\\ \Rightarrow A = \dfrac{{10\sin (90 - \varphi )}}{{\sin 30}}\end{array}\) Năng lượng dao động cực đại thì \({A_{max}} \Rightarrow \sin \left( {90 - \varphi } \right) = 1 \Rightarrow \varphi = 0\) Khi đó: \(\left\{ \begin{array}{l}A = \dfrac{{10\sin 90}}{{\sin 30}} = 20cm\\{A_2} = \dfrac{{10.\sin 60}}{{\sin 30}} = 10\sqrt 3 cm\end{array} \right.\)
Câu 13 :
Một vật dao động điều hòa có phương trình \(x = 5cos(2\pi t)\). Vận tốc của vật khi có li độ $x=3 cm$ là:
Đáp án : B Phương pháp giải :
Sử dụng hệ thức độc lập theo thời gian A-x-v: ${A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}}{\text{ }}$ Lời giải chi tiết :
Ta có: ${A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}{\text{ }} \to {\text{v = }} \pm \omega \sqrt {{A^2} - {x^2}} $ Thay \(A = 5cm,{\rm{ }}x = 3cm\), tần số góc: \(\omega = 2\pi \left( {rad/s} \right)\) $ \to {\text{v}} = \pm 2\pi \sqrt {{5^2} - {3^2}} = \pm 8\pi cm/s \approx \pm 25,12cm/s$
Câu 14 :
Chọn phát biểu sai trong các phương án sau:
Đáp án : C Lời giải chi tiết :
A, B, D – đúng C – sai vì: Dao động điều hòa là dao động trong đó li độ của vật là một hàm cosin (hay sin) của thời gian.
Câu 15 :
Trạng thái của dao động gồm yếu tố nào?
Đáp án : D Lời giải chi tiết :
Pha của dao động \(\left( {\omega t + \varphi } \right)\)cho biết trạng thái dao động (gồm li độ \(x\) và chiều chuyển động \(\overrightarrow v \) )
Câu 16 :
Một vật dao động điều hoà với phương trình \(x = 4cos\left( {4\pi t + \dfrac{\pi }{6}} \right)cm\). Tìm số lần vật qua vị trí có gia tốc là \(32{\pi ^2}\left( {cm/{s^2}} \right)\) theo chiều âm trong thời gian \(5,75s\) tính từ thời điểm gốc.
Đáp án : C Phương pháp giải :
+ Sử dụng công thức xác định chu kỳ T: \(T = \dfrac{{2\pi }}{\omega }\) + Xác định vị trí tại thời điểm $t = 0$ (x,v) Lời giải chi tiết :
Ta có: Chu kỳ dao động: \(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{4\pi }} = 0,5{\rm{s}}\) Tại $t = 0s$: \(\left\{ \begin{array}{l}x = 4c{\rm{os}}\left( {\dfrac{\pi }{6}} \right) = 2\sqrt 3 cm\\v = - A\omega \sin \left( {\dfrac{\pi }{6}} \right) < 0\end{array} \right.\) Tại vị trí có \(a = 32{\pi ^2}cm/{s^2} = - {\omega ^2}{x_2} \to {x_2} = - \dfrac{{32{\pi ^2}}}{{{{\left( {4\pi } \right)}^2}}} = - 2cm\) Trong một chu kỳ, vật đi qua vị trí $-2cm$ theo chiều âm $1$ lần Ta có: \({\rm{5}}{\rm{,75s}} = 11T + \dfrac{T}{2}\) Góc quét trong khoảng thời gian \(\dfrac{T}{2}\) kể từ thời điểm ban đầu: \(\Delta \varphi = \omega .\Delta t = \dfrac{{2\pi }}{T}.\dfrac{T}{2} = \pi \)
Trong khoảng thời gian \(\dfrac{T}{2}\) vật đi qua vị trí \( - 2cm\) theo chiều âm $1$ lần kể từ $t = 0$ => Trong \(5,75s\) đầu tiên, vật qua vị trí \( - 2cm\) số lần là: \(11 + 1 = 12\) lần
Câu 17 :
Một vật dao động điều hòa theo phương trình \(x = Acos\left( {\omega t} \right)\). Phát biểu nào sau đây sai khi nói về chuyển động của vật?
Đáp án : A Phương pháp giải :
+ Sử dụng trục thời gian suy ra từ đường tròn
+ Sử phương pháp đại số xác định quãng đường đi được của vật Lời giải chi tiết :
Tại thời điểm ban đầu \(t = 0\), ta có: \(x = Acos0 = A\) => Vật đang ở vị trí biên dương A - sai vì sau thời gian \(\dfrac{T}{8}\) vật ở vị trí có li độ \(x = \dfrac{{A\sqrt 2 }}{2} \to S = A - \dfrac{{A\sqrt 2 }}{2}\) B, C, D - đúng
Câu 18 :
Tại một nơi xác định, hai con lắc đơn có độ dài \({l_1}\) và \({l_2}\), dao động điều hoà với chu kì tương ứng \({T_1}\) và \({T_2}\). Tỉ số \(\dfrac{{{T_1}}}{{{T_2}}}\) bằng:
Đáp án : A Phương pháp giải :
Vận dụng biểu thức tính chu kì dao động của con lắc đơn: \(T = 2\pi \sqrt {\dfrac{l}{g}} \) Lời giải chi tiết :
Ta có: + Chu kì dao động của con lắc đơn có chiều dài \({l_1}\) : \({T_1} = 2\pi \sqrt {\dfrac{{{l_1}}}{g}} \) + Tần số dao động của con lắc đơn có chiều dài \({l_2}\): \({T_2} = 2\pi \sqrt {\dfrac{{{l_2}}}{g}} \) \( \to \dfrac{{{T_1}}}{{{T_2}}} = \sqrt {\dfrac{{{l_1}}}{{{l_2}}}} \)
Câu 19 :
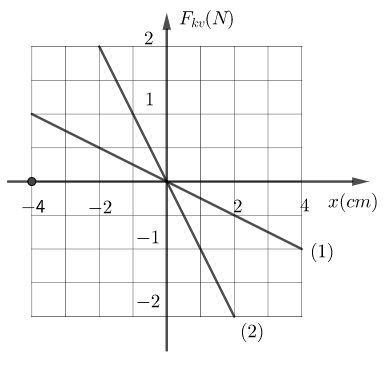
Hai con lắc lò xo nằm ngang dao động điều hòa dọc theo hai đường thẳng song song kề nhau và song song với trục Ox. Hai vật nặng có cùng khối lượng. Vị trí cân bằng của hai dao động đều nằm trên một đường thẳng qua gốc tọa độ và vuông góc với trục Ox. Đồ thị (1), (2) lần lượt biểu diễn mối liên hệ giữa lực kéo về Fkv và li độ x của con lắc 1 và con lắc 2. Biết tại thời điểm t, hai con lắc cùng qua vị trí cân bằng theo cùng một chiều. Sau đó một khoảng thời gian ngắn nhất bằng 0,5s con lắc 1 có động năng bằng một nửa cơ năng của nó, thì thế năng của con lắc 2 khi đó có giá trị gần nhất với giá trị nào sau đây?
Đáp án : C Phương pháp giải :
+ Đọc đồ thị F - x + Sử dụng lí thuyết về lực kéo về trong dao động điều hòa của con lắc lò xo + Áp dụng biểu thức lực kéo về cực đại: Fmax = kA Lời giải chi tiết :
+ Từ đồ thị ta thu được các dữ kiện sau: * CLLX1 có biên độ dao động \({A_1} = 4cm\), lực kéo về cực đại \({F_{1max}} = 1N\) => Độ cứng của lò xo 1 là \(k = \dfrac{{{F_{1max}}}}{{{A_1}}} = \dfrac{1}{{0,04}} = 25N/m\) * CLLX2 có biên độ dao động \({A_2} = 2cm\), lực kéo về cực đại \({F_{2max}} = 2N\) => Độ cứng của lò xo 2 là \({k_2} = \dfrac{{{F_{2max}}}}{{{A_2}}} = \dfrac{2}{{0,02}} = 100N/m\) + Theo đề bài, tại thời điểm ban đầu, cả hai con lắc đều đi qua VTCB theo một chiều, ở đây giả sử theo chiều dương. + Sau thời gian ngắn nhất \(t = 0,5s\) thì CLLX1 qua vị trí có động năng bằng nửa cơ năng, tức là vị trí \({x_1} = \dfrac{{{A_1}}}{{\sqrt 2 }}\) => Thời gian \(t = \dfrac{{{T_1}}}{8} \to {T_1} = 8t = 8.0,5 = 4s\) Và động năng khi đó của con lắc là \({{\rm{W}}_d} = \dfrac{{{{\rm{W}}_1}}}{2}{\rm{ = }}\dfrac{1}{2}\dfrac{{{k_1}{A_1}^2}}{2} = \dfrac{1}{2}\dfrac{{{{25.0,04}^2}}}{2} = 0,01(J)\) + Ta có \(\dfrac{{{T_2}}}{{{T_1}}} = \sqrt {\dfrac{{{k_1}}}{{{k_2}}}} = \sqrt {\dfrac{{25}}{{100}}} = > {T_2} = \dfrac{1}{2}{T_1} = 2s\) => Sau thời gian \(t = 0,5s = \dfrac{{{T_2}}}{4}\) => Khi đó CLLX 2 đang ở vị trí có li độ \({x_2} = {A_2} = 2cm\) => Thế năng của con lắc 2 là: \({{\rm{W}}_{t2}} = \dfrac{{{k_2}.x_2^2}}{2} = \dfrac{{{{100.0,02}^2}}}{2} = 0,02(J)\) Cơ năng của con lắc 2 là: \({\text{W}} = \dfrac{1}{2}{k_2}A_2^2 = \dfrac{1}{2}.100.0,{02^2} = 0,02\left( J \right)\) Do đó \(\dfrac{{{{\rm{W}}_{t2}}}}{{\rm{W}}} = 1\)
Câu 20 :
Chọn phát biểu đúng về tần số của hệ dao động tự do?
Đáp án : D Lời giải chi tiết :
Tần số của hệ dao động tự do chỉ phụ thuộc vào đặc tính của hệ dao động và không phụ thuộc vào các yếu tố bên ngoài
Câu 21 :
Một con lắc lò xo đang dao động tắt dần, cơ năng ban đầu của nó là \(6J\). Sau bốn chu kì kể từ lúc bắt đầu dao động thì biên độ của nó giảm đi \(24\% \). Phần cơ năng của con lắc chuyển hóa thành nhiệt năng tính trung bình trong mỗi chu kì dao động của nó là:
Đáp án : C Lời giải chi tiết :
+ Sau bốn chu kì dao động, biên độ còn lại của con lắc là: \({A_4} = A - 0,24A = 0,76A\) + Phần năng lượng bị mất đi sau bốn chu kì: \(\begin{array}{l}\Delta {E_4} = E - {E_4} = \frac{{E - {E_4}}}{E}E = \frac{{\frac{1}{2}k{A^2} - \frac{1}{2}kA_4^2}}{{\frac{1}{2}k{A^2}}}E\\ = \frac{{{A^2} - {{(0,76A)}^2}}}{{{A^2}}}.6 = 2,5344J\end{array}\) + Phần cơ năng chuyển hóa thành nhiệt năng trung bình trong mỗi chu kì: \(\Delta E = \frac{{2,5344}}{4} = 0,6336J\)
Câu 22 :
Chọn phát biểu đúng về sự biến đổi năng lượng của một chất điểm dao động điều hòa với chu kỳ \(T\), tần số \(f\)?
Đáp án : D Phương pháp giải :
Sử dụng lí thuyết về năng lượng của con lắc lò xo Lời giải chi tiết :
Ta có: + Động năng: \(\begin{array}{l}{W_d} = \dfrac{1}{2}m{v^2} = \dfrac{1}{2}m{\omega ^2}{A^2}{\sin ^2}(\omega t + \varphi )\\ = \dfrac{1}{2}m{\omega ^2}{A^2}\left( {\dfrac{{1 - c{\rm{os}}\left( {2\omega t + 2\varphi } \right)}}{2}} \right)\\ = \dfrac{1}{4}m{\omega ^2}{A^2} - \dfrac{1}{4}m{\omega ^2}{A^2}{\rm{cos}}\left( {2\omega t + 2\varphi } \right)\end{array}\) + Thế năng: \(\begin{array}{l}{W_t} = \dfrac{1}{2}k{x^2} = \dfrac{1}{2}k{A^2}{\rm{co}}{{\rm{s}}^2}(\omega t + \varphi )\\ = \dfrac{1}{2}k{A^2}\left( {\dfrac{{1 + c{\rm{os}}\left( {2\omega t + 2\varphi } \right)}}{2}} \right)\\ = \dfrac{1}{4}k{A^2} + \dfrac{1}{4}k{A^2}{\rm{cos}}\left( {2\omega t + 2\varphi } \right)\end{array}\) Từ các biểu thức của động năng và thế năng đó ta suy ra: Động năng và thế năng của vật biến thiên điều hòa với cùng tần số góc \(2\omega \), tần số \(2f\) và chu kì \(\dfrac{T}{2}\) . Cơ năng được bảo toàn => Các phương án: A, B, C – sai D – đúng
Câu 23 :
Một con lắc lò xo treo thẳng đứng lò xo có độ cứng \(k = 120N/m\), vật dao động có khối lượng \(m = 300g\), lấy gia tốc trọng trường \(g = {\pi ^2} = 10m/{s^2}\). Từ vị trí cân bằng kéo vật xuống một đoạn \(3cm\) rồi truyền cho vật vận tốc đầu \(80cm/s\) hướng thẳng đứng thì vật dao động điều hòa. Thời gian lò xo bị nén trong một chu kỳ là:
Đáp án : A Phương pháp giải :
+ Áp dụng biểu thức tính tần số góc của dao động: \(\omega = \sqrt {\dfrac{k}{m}} \) + Sử dụng hệ thức độc lập A-x-v: \({A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}\) + Áp dụng biểu thức tính độ dãn tại VTCB của lò xo treo thẳng đứng: \(\Delta l = \dfrac{{mg}}{k}\) + Sử dụng trục thời gian suy ra từ vòng tròn Lời giải chi tiết :
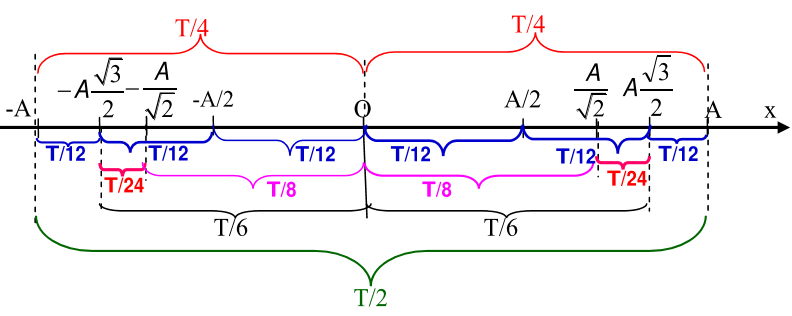
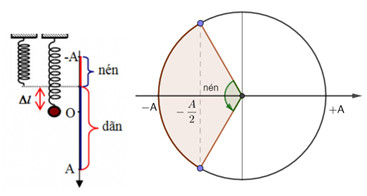
Ta có: + Tần số góc của dao động: \(\omega = \sqrt {\dfrac{k}{m}} = \sqrt {\dfrac{{120}}{{0,3}}} = 20(ra{\rm{d}}/s)\) + Biên độ dao động: \({A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} = {3^2} + {\left( {\dfrac{{80}}{{20}}} \right)^2} \to A = 5cm\) + Độ dãn của lò xo tại VTCB: \(\Delta l = \dfrac{{mg}}{k} = \dfrac{{0,3.10}}{{120}} = 0,025 = 2,5cm\) Chọn chiều dương hướng xuống, ta có:
=> Thời gian lò xo bị nén trong 1 chu kì là: \(t = 2\dfrac{T}{6} = \dfrac{T}{3} = \dfrac{{\dfrac{{2\pi }}{\omega }}}{3} = \dfrac{{2\pi }}{{20.3}} = \dfrac{\pi }{{30}}s\)
Câu 24 :
Tiến hành thí nghiệm do gia tốc trọng trường bằng con lắc đơn, một học sinh đo được chiều dài con lắc là \((119 \pm 1)\) (cm). Chu kì dao động nhỏ của nó là \((2,20 \pm 0,01)\) (s). Lấy \({\pi ^2} = 9,87\) và bỏ qua sai số của số π. Gia tốc trọng trường do học sinh đo được tại nơi làm thí nghiệm là:
Đáp án : C Phương pháp giải :
Áp dụng phương pháp tính sai số và công thức chu kỳ của con lắc đơn: \(T = 2\pi \sqrt {\dfrac{l}{g}} \) Lời giải chi tiết :
+ Áp dụng công thức: \(\overline T = 2\pi \sqrt {\dfrac{{\overline \ell }}{{\overline g }}} \Rightarrow \overline g = \dfrac{{4{\pi ^2}.\overline \ell }}{{{{\overline T }^2}}} = \dfrac{{4{\pi ^2}.1,19}}{{2,{{20}^2}}} = 9,706 \approx 9,7(m/{s^2}).\) + Sai số tương đối: \(\begin{array}{l}\delta = \dfrac{{\Delta g}}{{\overline g }} = \dfrac{{\Delta \ell }}{\ell } + 2.\dfrac{{\Delta T}}{T} = \dfrac{1}{{119}} + 2.\dfrac{{0,01}}{{2,20}} = 0,0175\\ \Rightarrow \Delta g = \overline g .\delta = 9,7.0,0175 \approx 0,16975 \approx 0,2\end{array}\) + Gia tốc: \(g = \overline g \pm \Delta g = (9,7 \pm 0,2)(m/{s^2})\)
Câu 25 :
Khi nói về dao động cơ tắt dần, phát biểu nào sau đây sai?
Đáp án : B Phương pháp giải :
Tốc độ của vật trong dao động tắt dần biến đổi tuần hoàn nên động năng cũng biến đổi thuần hoàn Lời giải chi tiết :
Tốc độ của vật trong dao động tắt dần biến đổi tuần hoàn nên động năng cũng biến đổi thuần hoàn Vì vậy nói Dao động tắt dần có động năng giảm dần theo thời gian là sai |




















Danh sách bình luận