Đề kiểm tra giữa học kì 2 - Đề số 3Đề bài
Câu 1 :
Dao động điện từ trong mạch chọn sóng của máy thu khi máy thu bắt được sóng là:
Câu 2 :
Tìm phát biểu sai. Dao động điện từ trong mạch dao động LC bị tắt dần là do:
Câu 3 :
Sóng điện từ
Câu 4 :
Trong chân không, tia tử ngoại có bước sóng trong khoảng:
Câu 5 :
Mạch dao động điện từ điều hoà gồm cuộn cảm L và tụ điện C. Khi tăng độ tự cảm của cuộn cảm lên 2 lần và giảm điện dung của tụ điện đi 2 lần thì tần số dao động của mạch
Câu 6 :
Trong thí nghiệm Y-âng về giao thoa ánh sáng, khoảng cách giữa hai khe là a, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là D. Khi nguồn sóng phát bức xạ đơn sắc có bước sóng λ thì khoảng vân giao thoa trên màn là i. Hệ thức nào sau đây đúng?
Câu 7 :
Cường độ dòng điện tức thời trong mạch dao động LC có dạng i = 0,05sin2000t(A). Tần số góc dao động của mạch là
Câu 8 :
Quang phổ liên tục:
Câu 9 :
Mạch dao động LC gồm cuộn dây thuần cảm có độ tự cảm \(L = 2mH\) và tụ điện có điện dung \(C = 5pF\) Tụ được tích điện đến hiệu điện thế 10V, sau đó người ta để cho tụ phóng điện trong mạch. Nếu chọn gốc thời gian là lúc tụ bắt đầu phóng điện thì biểu thức của điện tích trên bản tụ điện là:
Câu 10 :
Nếu quy ước: 1- chọn sóng; 2- tách sóng; 3- khuyếch đại âm tần; 4- khuyếch đại cao tần; 5-chuyển thành sóng âm. Việc thu sóng điện từ trong máy thu thanh phải qua các giai đoạn nào, với thứ tự nào?
Câu 11 :
Phát biểu nào sau đây là đúng khi nói về quang phổ?
Câu 12 :
Phát biểu nào sai khi nói về sóng điện từ?
Câu 13 :
Một mạch chọn sóng gồm cuộn dây có hệ số tự cảm không đổi và một tụ điện có điện dung biến thiên. Khi điện dung của tụ là 20nF thì mạch thu được bước sóng 40m. Nếu muốn thu được bước sóng 60m thì phải điều chỉnh điện dung của tụ
Câu 14 :
Góc chiết quang của lăng kính bằng A = 60. Chiếu một tia sáng trắng vào mặt bên của lăng kính theo phương vuông góc với mặt phẳng phân giác của góc chiết quang. Đặt một màn quan sát, sau lăng kính, song song với mặt phẳng phân giác của góc chiết quang của lăng kính và cách mặt này 2m. Chiết suất của lăng kính đối với tia đỏ là nd = 1,5 và đối với tia tím là nt = 1,56 . Độ rộng của quang phổ liên tục trên màn quan sát bằng
Câu 15 :
Trong thí nghiệm giao thoa ánh sáng bằng hai khe Y-âng trong không khí người ta thấy tại M trên màn có vân sáng bậc 3. Nếu nhúng toàn bộ hệ thống vào trong nước có chiết suất n = 4/3 thì tại M ta thu được vân gì?
Câu 16 :
Một chùm electron, sau khi được tăng tốc từ trạng thái đứng yên bằng hiệu điện thế không đổi U, đến đập vào một kim loại làm phát ra tia X. Cho bước sóng nhỏ nhất của chùm tia X này là 6,8.10-11 m. Giá trị của U bằng.
Câu 17 :
Trong thí nghiệm Iâng về giao thoa ánh sáng, ban đầu dùng nguồn sáng S có bước sóng \({\lambda _1}\) = 0,4\({\rm{\mu m}}\). Sau đó tắt bức xạ \({\lambda _1}\), thay bằng bức xạ \({\lambda _2} \ne \)\({\lambda _1}\) thì tại vị trí vân sáng bậc 3 của bức xạ \({\lambda _1}\) ta quan sát được một vân sáng của bức xạ \({\lambda _2}\). Bước sóng \({\lambda _2}\) bằng:
Câu 18 :
Một tụ điện có điện dung C được nạp điện tới điện tích q. Khi nối tụ với cuộn cảm thuần có độ tự cảm L1 thì trong mạch có dao động điện từ riêng với cường độ dòng điện cực đại bằng 70mA. Khi nối tụ với cuộn cảm thuần có độ tự cảm L2 thì trong mạch có dao động điện từ riêng với cường độ dòng điện cực dại bằng 35mA. Nếu nối tụ với cuộn cảm thuần có độ tự cảm ${L_3} = 13{L_1} + 9{L_2}$ thì trong mạch có cường độ dòng điện cực đại bằng
Câu 19 :
Vệ tinh viễn thông địa tĩnh Vinasat-1 nằm trên quỹ đạo địa tĩnh (là quỹ đạo tròn trên xích đạo của Trái Đất (vĩ độ \({0^0}\)) ở cách bề mặt Trái Đất \(35000{\rm{ }}km\) và có kinh độ \({132^0}\)Đ. Một sóng truyền hình phát từ Đài truyền hình Hà Nội ở tọa độ (\({21^0}01'\) B, \({105^0}48'\)Đ ) truyền lên vệ tinh, rồi tức thì truyền đến đài truyền hình Cần Thơ ở tọa độ (\({10^0}01'\)B, \({105^0}48'\)Đ) . Cho bán kính của Trái Đất là \(6400km\) và tốc độ truyền sóng trung bình là \(\dfrac{8}{3}{.10^8}m/s\). Bỏ qua độ cao của anten phát và aten thu ở các Đài truyền hình so với bán kình Trái Đất. Thời gian từ lúc truyền sóng đến nhận sóng gần giá trị nào nhất sau đây?
Câu 20 :
Trong thí nghiệm Y-âng về giao thoa ánh sáng, nếu thay ánh sáng đơn sắc màu lam bằng ánh sáng đơn sắc màu chàm và giữ nguyên các điều kiện khác thì trên màn quan sát
Câu 21 :
Cho 4 tia có bước sóng như sau qua cùng một lăng kính, tia nào lệch ít nhất so với phương truyền ban đầu:
Câu 22 :
Trong thí nghiệm Y-âng về giao thoa ánh sáng, hai khe được chiếu sáng đồng thời bởi hai bức xạ đơn sắc có bước sóng lần lượt là \({\lambda _1}\) và \({\lambda _2}\). Trên màn quan sát có vân sáng bậc 12 của \({\lambda _1}\) trùng với vân sáng bậc 9 của \({\lambda _2}\). Tỉ số \(\dfrac{{{\lambda _1}}}{{{\lambda _2}}}\) bằng:
Câu 23 :
Thực hiện giao thoa ánh sáng với thiết bị của Y-âng, khoảng cách giữa hai khe a = 2mm, từ hai khe đến màn là D = 2m. Người ta chiếu sáng hai khe bằng ánh sáng trắng (380nm ≤ λ ≤ 760nm). Quan sát điểm M trên màn ảnh, cách vân trung tâm 3mm. Tại M bức xạ cho vân sáng có bước sóng dài nhất bằng
Câu 24 :
Thực hiện thí nghiệm giao thoa Y – âng với ánh sáng đơn sắc có bước sóng \(560nm\). Khoảng cách giữa hai khe S1S2 là \(1mm\). Khoảng cách từ mặt phẳng chứa hai khe đến màn là \(2,5m\). Goi M và N là hai điêmt trên trường giao thoa, cách vân sáng trung tâm lần lượt là \(107,25mm\) và \(82,5mm\). Lúc \(t = 0\) bắt đầu cho màn dịch chuyển thẳng đều theo phương vuông góc với mặt phẳng chứa hai khe và ra xa S1S2 với tốc độ \(5cm/s\). Gọi t1 là thời điểm đầu tiên mà tại M và N đồng thời cho vân sáng. Gọi t2 là thời điểm đầu tiên mà tại M cho vân tối, đồng thời tại N cho vân sáng. Khoảng thời gian \(\Delta t = \left| {{t_1} - {t_2}} \right|\) có giá trị gần nhất với giá trị nào sau đây ?
Câu 25 :
Tia hồng ngoại được dùng
Lời giải và đáp án
Câu 1 :
Dao động điện từ trong mạch chọn sóng của máy thu khi máy thu bắt được sóng là:
Đáp án : B Phương pháp giải :
Vận dụng lí thuyết về mạch chọn sóng vô tuyến Lời giải chi tiết :
Dao động điện từ trong mạch chọn sóng của máy thu khi máy thu bắt được sóng là : Dao động cưỡng bức có tần số bằng tần số riêng của mạch
Câu 2 :
Tìm phát biểu sai. Dao động điện từ trong mạch dao động LC bị tắt dần là do:
Đáp án : D Lời giải chi tiết :
A, B, C - đúng Mạch dao động điện từ tự do (mạch dao động LC lí tưởng) có năng lượng điện trường tập trung trong tụ điện và năng lượng từ trường tập trung trong cuộn cảm. Hai năng lượng này luôn chuyển hóa lẫn nhau => Sự chuyển hóa năng lượng điện trường sang từ trường và ngược lại không là nguyên nhân gây tắt dần dao động => D - sai
Câu 3 :
Sóng điện từ
Đáp án : B Phương pháp giải :
Xem lí thuyết mục 2- phần II Lời giải chi tiết :
Sóng điện từ là điện từ trường lan truyền trong không gian.
Câu 4 :
Trong chân không, tia tử ngoại có bước sóng trong khoảng:
Đáp án : A Lời giải chi tiết :
Trong chân không, tia tử ngoại có bước sóng trong khoảng từ vài nanômét đến 380 nm (ngắn hơn bước sóng của ánh sáng tím)
Câu 5 :
Mạch dao động điện từ điều hoà gồm cuộn cảm L và tụ điện C. Khi tăng độ tự cảm của cuộn cảm lên 2 lần và giảm điện dung của tụ điện đi 2 lần thì tần số dao động của mạch
Đáp án : A Phương pháp giải :
Vận dụng biểu thức xác định tần số dao động của mạch dao động điện từ LC: $f = \frac{1}{{2\pi \sqrt {LC} }}$ Lời giải chi tiết :
Ta có, tần số dao động của mạch LC dao động tự do: $f = \frac{1}{{2\pi \sqrt {LC} }}$ => Khi tăng L lên 2 lần, điện dung C giảm 2 lần => thì tần số của dao động không đổi
Câu 6 :
Trong thí nghiệm Y-âng về giao thoa ánh sáng, khoảng cách giữa hai khe là a, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là D. Khi nguồn sóng phát bức xạ đơn sắc có bước sóng λ thì khoảng vân giao thoa trên màn là i. Hệ thức nào sau đây đúng?
Đáp án : C Phương pháp giải :
Sử dụng công thức tính khoảng vân Lời giải chi tiết :
Ta có:\(i = \frac{{\lambda D}}{a} \Rightarrow \lambda = \frac{{a.i}}{D}\)
Câu 7 :
Cường độ dòng điện tức thời trong mạch dao động LC có dạng i = 0,05sin2000t(A). Tần số góc dao động của mạch là
Đáp án : C Phương pháp giải :
Đọc phương trình cường độ dòng điện trong mạch dao động LC Lời giải chi tiết :
Từ phương trình cường độ dòng điện trong mạch dao động LC i = 0,05sin2000t(A). Ta có, ω = 2000 (rad/s)
Câu 8 :
Quang phổ liên tục:
Đáp án : B Phương pháp giải :
Sử dụng lí thuyết về đặc điểm của quang phổ liên tục Lời giải chi tiết :
Ta có: Quang phổ liên tục có đặc điểm: - Chỉ phụ thuộc vào nhiệt độ nguồn (t>20000C) - Không phụ thuộc vào cấu tạo của nguồn sáng - Nhiệt độ càng lớn: năng lượng tập trung nhiều ở vùng ánh sáng có λ ngắn.
Câu 9 :
Mạch dao động LC gồm cuộn dây thuần cảm có độ tự cảm \(L = 2mH\) và tụ điện có điện dung \(C = 5pF\) Tụ được tích điện đến hiệu điện thế 10V, sau đó người ta để cho tụ phóng điện trong mạch. Nếu chọn gốc thời gian là lúc tụ bắt đầu phóng điện thì biểu thức của điện tích trên bản tụ điện là:
Đáp án : A Phương pháp giải :
+ Áp dụng công thức tính tần số góc: \(\omega = \frac{1}{{\sqrt {LC} }}\) + Áp dụng biểu thức: \({U_0} = \frac{{{q_0}}}{C}\) + Xác định pha ban đầu của dao động Lời giải chi tiết :
Ta có: + Tần số góc của dao động: \(\omega = \frac{1}{{\sqrt {LC} }} = \frac{1}{{\sqrt {{{2.10}^{ - 3}}{{.5.10}^{ - 12}}} }} = {10^7}(ra{\rm{d}}/s)\) + Điện tích cực đại: \({U_0} = \frac{{{q_0}}}{C} \to {q_0} = {U_0}C = {10.5.10^{ - 12}} = {5.10^{ - 11}}C\) + Tại t = 0: \(q = {q_0} \to {\varphi _q} = 0\) => Biểu thức điện tích trên bản tụ là: \(q = {5.10^{ - 11}}c{\rm{os}}\left( {{{10}^7}t} \right)C\)
Câu 10 :
Nếu quy ước: 1- chọn sóng; 2- tách sóng; 3- khuyếch đại âm tần; 4- khuyếch đại cao tần; 5-chuyển thành sóng âm. Việc thu sóng điện từ trong máy thu thanh phải qua các giai đoạn nào, với thứ tự nào?
Đáp án : C Phương pháp giải :
Xem lí thuyết phần 2 Lời giải chi tiết :
Các giai đoạn trong máy thu thanh: - Anten thu: Thu sóng điện từ cao tần biến điệu. - Mạch khuyếch đại dao động điện từ cao tần: Khuếch đại dao động điện từ cao tần. - Mạch tách sóng: Tách dao động điện từ âm tần ra khỏi dao động điện từ cao tần. - Mạch khuếch đại dao động điện từ âm tần: Khuếch đại dao động điện từ âm tần từ mạch tách sóng gửi đến. - Loa: Biến dao động điện thành dao động âm => Thứ tự ta cần sắp xếp là: 1 - 4 - 2 - 3 - 5
Câu 11 :
Phát biểu nào sau đây là đúng khi nói về quang phổ?
Đáp án : B Phương pháp giải :
Vận dụng lí thuyết về các loại quang phổ Lời giải chi tiết :
A - sai vì quang phổ liên tục không phụ thuộc vào thành phần cấu tạo của nguồn sáng B - đúng C - sai vì để thu được quang phổ vạch hấp thụ thì nhiệt độ của đám khí hay hơi hấp thụ phải thấp hơn nhiệt độ của nguồn sáng phát ra quang phổ liên tục D - sai vì quang phổ vạch hấp thụ là quang phổ của ánh sáng do khi chiếu ánh sáng trắng qua nguồn khí hay hơi có nhiệt độ thấp hơn của nguồn
Câu 12 :
Phát biểu nào sai khi nói về sóng điện từ?
Đáp án : B Phương pháp giải :
Sử dụng lí thuyết về sóng điện từ Lời giải chi tiết :
A, C, D - đúng B - sai vì: Dao động của điện trường và của từ trường tại một điểm luôn luôn đồng pha với nhau.
Câu 13 :
Một mạch chọn sóng gồm cuộn dây có hệ số tự cảm không đổi và một tụ điện có điện dung biến thiên. Khi điện dung của tụ là 20nF thì mạch thu được bước sóng 40m. Nếu muốn thu được bước sóng 60m thì phải điều chỉnh điện dung của tụ
Đáp án : C Phương pháp giải :
Áp dụng biểu thức tính bước sóng: \(\lambda = 2\pi c\sqrt {LC} \) Lời giải chi tiết :
Ta có: \(\lambda = 2\pi c\sqrt {LC} \) + Khi C = C1 = 20nF: \({\lambda _1} = 2\pi c\sqrt {L{C_1}} \) + Khi C = C2: \({\lambda _2} = 2\pi c\sqrt {L{C_2}} \) \[ \to \frac{{{\lambda _1}}}{{{\lambda _2}}} = \sqrt {\frac{{{C_1}}}{{{C_2}}}} = \frac{{40}}{{60}} = \frac{2}{3} \to \frac{{{C_1}}}{{{C_2}}} = \frac{4}{9} \to {C_2} = \frac{9}{4}{C_1} = \frac{9}{4}.20nF = 45nF\] => Cần tăng điện dung của tụ lên một khoảng bằng 45nF - 20nF = 25nF
Câu 14 :
Góc chiết quang của lăng kính bằng A = 60. Chiếu một tia sáng trắng vào mặt bên của lăng kính theo phương vuông góc với mặt phẳng phân giác của góc chiết quang. Đặt một màn quan sát, sau lăng kính, song song với mặt phẳng phân giác của góc chiết quang của lăng kính và cách mặt này 2m. Chiết suất của lăng kính đối với tia đỏ là nd = 1,5 và đối với tia tím là nt = 1,56 . Độ rộng của quang phổ liên tục trên màn quan sát bằng
Đáp án : B Phương pháp giải :
Áp dụng công thức tính bề rộng quang phổ: \(\Delta x = {x_t} - {x_d} = \left( {{n_t} - {n_d}} \right)LA\) Lời giải chi tiết :
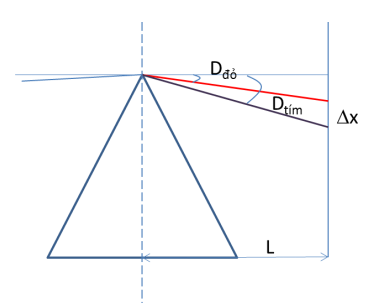 Ta có: \({{\mathop{\rm tanD}\nolimits} _d} = \frac{{{x_d}}}{L},{\rm{ }}{{\mathop{\rm tanD}\nolimits} _t} = \frac{{{x_t}}}{L}\) Vì A≪ \( \to \left\{ \begin{array}{l}{D_d} \ll \\{D_t} \ll \end{array} \right. \to {\mathop{\rm tanD}\nolimits} \approx sinD \approx D\) \(\begin{array}{l}\Delta x = {x_t} - {{\rm{x}}_d} = ({n_t} - 1)AL - ({n_d} - 1)AL\\ = ({n_t} - {n_d})LA = (1,56 - 1,5)2.\frac{{6\pi }}{{180}} = 0,01257m = 12,57mm\end{array}\) Chú ý
Đổi độ sang rad
Câu 15 :
Trong thí nghiệm giao thoa ánh sáng bằng hai khe Y-âng trong không khí người ta thấy tại M trên màn có vân sáng bậc 3. Nếu nhúng toàn bộ hệ thống vào trong nước có chiết suất n = 4/3 thì tại M ta thu được vân gì?
Đáp án : B Phương pháp giải :
+ Áp dụng công thức khoảng vân trong môi trường có chiết suất n: \(i' = \frac{{{i_{kk}}}}{n}\) + Áp dụng biểu thức xác định vị trí vân sáng - tối trên màn Lời giải chi tiết :
Gọi : i, i’ lần lượt là khoảng vân của ánh sáng trong không khí và trong nước Ta có: + \(i' = \frac{i}{n}\) + Khi đặt hệ trong không khí: xM = 3i + Khi đặt hệ trong môi trường nước: \({x_M} = 3i = 3i'.n = 3.\frac{4}{3}i' = 4i'\) => Khi nhúng toàn bộ hệ thống vào trong nước thì tại M là vân sáng bậc 4
Câu 16 :
Một chùm electron, sau khi được tăng tốc từ trạng thái đứng yên bằng hiệu điện thế không đổi U, đến đập vào một kim loại làm phát ra tia X. Cho bước sóng nhỏ nhất của chùm tia X này là 6,8.10-11 m. Giá trị của U bằng.
Đáp án : A Phương pháp giải :
Áp dụng biểu thức: \(eU = \dfrac{{hc}}{\lambda }\) Lời giải chi tiết :
Ta có: \(\begin{array}{l}eU = \dfrac{{hc}}{\lambda }\\ \Rightarrow U = \dfrac{{hc}}{{e\lambda }} = \dfrac{{6,{{625.10}^{ - 34}}{{.3.10}^8}}}{{1,{{6.10}^{ - 19}}.6,{{8.10}^{ - 11}}}} \\= 18267,5V \approx 18,3kV\end{array}\)
Câu 17 :
Trong thí nghiệm Iâng về giao thoa ánh sáng, ban đầu dùng nguồn sáng S có bước sóng \({\lambda _1}\) = 0,4\({\rm{\mu m}}\). Sau đó tắt bức xạ \({\lambda _1}\), thay bằng bức xạ \({\lambda _2} \ne \)\({\lambda _1}\) thì tại vị trí vân sáng bậc 3 của bức xạ \({\lambda _1}\) ta quan sát được một vân sáng của bức xạ \({\lambda _2}\). Bước sóng \({\lambda _2}\) bằng:
Đáp án : C Phương pháp giải :
Công thức xác định vị trí vân sáng : xs = kλD/a Lời giải chi tiết :
Ta có : \({x_1} = {x_2} \Leftrightarrow \frac{{{k_1}{\lambda _1}D}}{a} = \frac{{{k_2}{\lambda _2}D}}{a} \Rightarrow {k_1}{\lambda _1} = {k_2}{\lambda _2} \Rightarrow {\lambda _2} = \frac{{1,2}}{{{k_2}}}\) k2 phải nguyên => λ2 = 0,6 µm (k2 = 2)
Câu 18 :
Một tụ điện có điện dung C được nạp điện tới điện tích q. Khi nối tụ với cuộn cảm thuần có độ tự cảm L1 thì trong mạch có dao động điện từ riêng với cường độ dòng điện cực đại bằng 70mA. Khi nối tụ với cuộn cảm thuần có độ tự cảm L2 thì trong mạch có dao động điện từ riêng với cường độ dòng điện cực dại bằng 35mA. Nếu nối tụ với cuộn cảm thuần có độ tự cảm ${L_3} = 13{L_1} + 9{L_2}$ thì trong mạch có cường độ dòng điện cực đại bằng
Đáp án : A Phương pháp giải :
+ Áp dụng biểu thức tính cường độ dòng điện cực đại: I0 = ωq0 + Áp dụng biểu thức xác định tần số góc của mạch dao động LC: $\omega = \frac{1}{{\sqrt {LC} }}$ Lời giải chi tiết :
Cách 1 : Ta có: \(\begin{array}{l}{I_1} = {\omega _1}q = \frac{q}{{\sqrt {{L_1}C} }} = > {L_1} = \frac{{{q^2}}}{{{I_1}^2C}}\\{I_2} = {\omega _2}q = \frac{q}{{\sqrt {{L_2}C} }} = > {L_2} = \frac{{{q^2}}}{{{I_2}^2C}}\end{array}\) => Khi sử dụng cuộn cảm có độ tự cảm \({L_3} = 13{L_1} + 9{L_2}\) thì cường độ dòng điện cực đại là : \({I_3} = \frac{q}{{\sqrt {{L_3}C} }} = \frac{q}{{\sqrt {(13\frac{{{q^2}}}{{{I_1}^2C}} + 9\frac{{{q^2}}}{{{I_2}^2C}})C} }} = \frac{{{I_1}{I_2}}}{{\sqrt {13{I_2}^2 + 9{I_1}^2} }} = 10mA\) Cách 2: Ta có: \(\begin{array}{l}{I_1} = {\omega _1}q = \frac{q}{{\sqrt {{L_1}C} }};{I_2} = {\omega _2}q = \frac{q}{{\sqrt {{L_2}C} }}\\ \to \frac{{{I_1}}}{{{I_2}}} = \sqrt {\frac{{{L_2}}}{{{L_1}}}} = \frac{{70}}{{35}} \to \frac{{{L_2}}}{{{L_1}}} = 4\\ \to {L_2} = 4{L_1}\end{array}\) \(\begin{array}{l}{I_3} = \frac{q}{{\sqrt {{L_3}C} }} \to \frac{{{I_3}}}{{{I_1}}} = \sqrt {\frac{{{L_1}}}{{{L_3}}}} = \sqrt {\frac{{{L_1}}}{{13{L_1} + 9{L_2}}}} = \sqrt {\frac{{{L_1}}}{{13{L_1} + 9.4{L_1}}}} = \frac{1}{7}\\ \to {I_3} = \frac{{{I_1}}}{7} = \frac{{70}}{7} = 10mA\end{array}\)
Câu 19 :
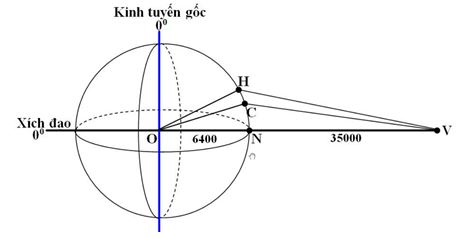
Vệ tinh viễn thông địa tĩnh Vinasat-1 nằm trên quỹ đạo địa tĩnh (là quỹ đạo tròn trên xích đạo của Trái Đất (vĩ độ \({0^0}\)) ở cách bề mặt Trái Đất \(35000{\rm{ }}km\) và có kinh độ \({132^0}\)Đ. Một sóng truyền hình phát từ Đài truyền hình Hà Nội ở tọa độ (\({21^0}01'\) B, \({105^0}48'\)Đ ) truyền lên vệ tinh, rồi tức thì truyền đến đài truyền hình Cần Thơ ở tọa độ (\({10^0}01'\)B, \({105^0}48'\)Đ) . Cho bán kính của Trái Đất là \(6400km\) và tốc độ truyền sóng trung bình là \(\dfrac{8}{3}{.10^8}m/s\). Bỏ qua độ cao của anten phát và aten thu ở các Đài truyền hình so với bán kình Trái Đất. Thời gian từ lúc truyền sóng đến nhận sóng gần giá trị nào nhất sau đây?
Đáp án : C Phương pháp giải :
+ Đọc kinh độ và vĩ độ địa lý: Kinh độ là đường thẳng đứng, vĩ độ là đường nằm ngang + Vận dụng các biểu thức trong tam giác với góc nhỏ + Vận dụng biểu thức liên hệ giữa quãng đường – thời gian: \(s = vt\) Lời giải chi tiết :
Kí hiệu vệ tinh là \(\left( V \right)\), do vệ tinh có vĩ độ \({0^0}\) nên đang nằm trên đường xích đạo Hà Nội \(\left( H \right)\) và Cần Thơ \(\left( C \right)\) có cùng kinh độ, nhưng vĩ độ khác nhau, ta biểu diễn được trên hình. + \(\widehat {CON} = {10^0}01'\) chính là vĩ độ của \(\left( C \right)\) Ta suy ra: \(CN = R.\widehat {CON} = 6400.\dfrac{{{{10}^0}01'.\pi }}{{180}} = 1118,87km\) + \(\widehat {HON} = {21^0}01'\) chính là vĩ độ của \(\left( H \right)\) Ta suy ra: \(HN = R.\widehat {HON} = 6400.\dfrac{{{{21}^0}01'.\pi }}{{180}} = 2347,58km\) Do \(\left( H \right)\) và \(\left( C \right)\) cùng kinh độ. Xem \(\left( N \right)\) có cùng kinh độ với \(\left( H \right)\) và \(\left( C \right)\) và \(HC \bot OV\) Ta có: + \(HV = \sqrt {H{N^2} + N{V^2}} = \sqrt {{{2347,58}^2} + {{35000}^2}} = 35078,64km\) + \(CV = \sqrt {C{N^2} + N{V^2}} = \sqrt {{{1118,87}^2} + {{35000}^2}} = 35017,88km\) Quãng đường sóng truyền đi: \(s = HV + CV = 35078,64 + 35017,88 = 70096,52km = 70096520m\) Vậy thời gian truyền sóng: \(t = \dfrac{s}{v} = \dfrac{{70096520}}{{\dfrac{8}{3}{{.10}^8}}} = 0,2628s\)
Câu 20 :
Trong thí nghiệm Y-âng về giao thoa ánh sáng, nếu thay ánh sáng đơn sắc màu lam bằng ánh sáng đơn sắc màu chàm và giữ nguyên các điều kiện khác thì trên màn quan sát
Đáp án : B Phương pháp giải :
Sử dụng công thức tính khoảng vân \(i = \dfrac{{\lambda D}}{a}\) để đánh giá Lời giải chi tiết :
Ta có, + Khoảng vân: \(i = \dfrac{{\lambda D}}{a}\) + \({\lambda _{lam}} > {\lambda _{cham}}\) => Khi thay ánh sáng lam bằng ánh sáng chàm, \(a,D\) - không đổi, bước sóng giảm đi => Khoảng vân \(i\) giảm xuống
Câu 21 :
Cho 4 tia có bước sóng như sau qua cùng một lăng kính, tia nào lệch ít nhất so với phương truyền ban đầu:
Đáp án : D Phương pháp giải :
+ Sử dụng tính chất chiết suất của ánh sáng trong các chất trong suốt: \(\left( {{n_{do}} < {n_{cam}} < {n_{vang}} < {n_{luc}} < {n_{lam}} < {n_{cham}} < {n_{tim}}} \right)\) + Vận dụng lí thuyết về khúc xạ ánh sáng: Ánh sáng đi từ môi trường chiết quang kém sang môi trường chiết quang hơn thì tia khúc xạ gần pháp tuyến hơn so với tia tới + Bước sóng ánh sáng giảm dần từ đỏ đến tím Lời giải chi tiết :
Ta có: + Chiết suất của các chất trong suốt biến thiên theo màu sắc của ánh sáng và tăng dần từ màu đỏ đến màu tím \(\left( {{n_{do}} < {n_{cam}} < {n_{vang}} < {n_{luc}} < {n_{lam}} < {n_{cham}} < {n_{tim}}} \right)\) + Theo định luật khúc xạ ánh sáng: Ánh sáng đi từ môi trường chiết quang kém sang môi trường chiết quang hơn thì tia khúc xạ gần pháp tuyến hơn so với tia tới, ta có hình ảnh khúc xạ của các tia sáng: 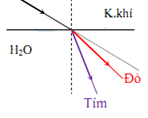 Tia tím xa phương truyền ban đầu nhất, tia đỏ gần phương truyền ban đầu nhất => Ánh sáng từ đỏ đến tím có góc lệch so với phương truyền ban đầu tăng dần Mà từ đỏ đến tím ta có bước sóng giảm dần => Trong 4 tia có bước sóng trên thì tia có bước sóng \(0,6\mu m\) bị lệch ít nhất so với phương truyền ban đầu
Câu 22 :
Trong thí nghiệm Y-âng về giao thoa ánh sáng, hai khe được chiếu sáng đồng thời bởi hai bức xạ đơn sắc có bước sóng lần lượt là \({\lambda _1}\) và \({\lambda _2}\). Trên màn quan sát có vân sáng bậc 12 của \({\lambda _1}\) trùng với vân sáng bậc 9 của \({\lambda _2}\). Tỉ số \(\dfrac{{{\lambda _1}}}{{{\lambda _2}}}\) bằng:
Đáp án : D Phương pháp giải :
+ Sử dụng công thức hai vân trùng nhau: \({x_1} = {\rm{ }}{x_2}\) + Vị trí vân sáng: \({x_S} = ki = k\dfrac{{\lambda D}}{a}\) Lời giải chi tiết :
Tại vị trí vân trùng ta có: \(12{i_1} = 9{i_2} \Leftrightarrow 12{\lambda _1} = {\rm{ }}9{\lambda _2} \Rightarrow \dfrac{{{\lambda _1}}}{{{\lambda _2}}} = \dfrac{3}{4}\)
Câu 23 :
Thực hiện giao thoa ánh sáng với thiết bị của Y-âng, khoảng cách giữa hai khe a = 2mm, từ hai khe đến màn là D = 2m. Người ta chiếu sáng hai khe bằng ánh sáng trắng (380nm ≤ λ ≤ 760nm). Quan sát điểm M trên màn ảnh, cách vân trung tâm 3mm. Tại M bức xạ cho vân sáng có bước sóng dài nhất bằng
Đáp án : D Phương pháp giải :
+ Sử dụng lí thuyết về giao thoa sóng ánh sáng + Vị trí vân sáng: \({x_s} = k\dfrac{{\lambda D}}{a}\) Lời giải chi tiết :
+ Tọa độ của điểm M \({x_M} = k\dfrac{{\lambda D}}{a} = > \lambda = \dfrac{{a.{x_M}}}{{kD}} = \dfrac{{2.3}}{{2k}} = \dfrac{3}{k}(\mu m)\) Mà: \(0,38 \le \lambda \le 0,76 \\= > 0,38 \le \dfrac{3}{k} \le 0,76 \\= > 3,9 \le k \le 7,8 \\\Rightarrow k = {\rm{ }}4,5,6,7\) Bức xạ cho vân sáng tại M có bước sóng lớn nhất (ứng với k nhỏ nhất) là: \({\lambda _{\max }} = \dfrac{3}{{{k_{\min }}}} = \dfrac{3}{4} = 0,75(\mu m) = 750(nm)\)
Câu 24 :
Thực hiện thí nghiệm giao thoa Y – âng với ánh sáng đơn sắc có bước sóng \(560nm\). Khoảng cách giữa hai khe S1S2 là \(1mm\). Khoảng cách từ mặt phẳng chứa hai khe đến màn là \(2,5m\). Goi M và N là hai điêmt trên trường giao thoa, cách vân sáng trung tâm lần lượt là \(107,25mm\) và \(82,5mm\). Lúc \(t = 0\) bắt đầu cho màn dịch chuyển thẳng đều theo phương vuông góc với mặt phẳng chứa hai khe và ra xa S1S2 với tốc độ \(5cm/s\). Gọi t1 là thời điểm đầu tiên mà tại M và N đồng thời cho vân sáng. Gọi t2 là thời điểm đầu tiên mà tại M cho vân tối, đồng thời tại N cho vân sáng. Khoảng thời gian \(\Delta t = \left| {{t_1} - {t_2}} \right|\) có giá trị gần nhất với giá trị nào sau đây ?
Đáp án : C Phương pháp giải :
+ Vị trí vân sáng và vân tối : \(\left\{ \begin{array}{l}{x_s} = ki = k\dfrac{{\lambda D}}{a}\\{x_t} = \left( {k + \dfrac{1}{2}} \right)i = \left( {k + \dfrac{1}{2}} \right).\dfrac{{\lambda D}}{a}\end{array} \right.\) + Công thức liên hệ giữa S, v và t : \(S = v.t\) Lời giải chi tiết :
+ Lúc \(t = 0\) bắt đầu cho màn dịch chuyển thẳng đều theo phương vuông góc với mặt phẳng chứa hai khe và ra xa S1S2 với tốc độ \(5cm/s\) + t1 là thời điểm đầu tiên mà tại M và N đồng thời cho vân sáng. Ta có: \(\begin{array}{l}\left\{ \begin{array}{l}{x_M} = 107,25 = \dfrac{{{k_1}.0,56.\left( {2,5 + 0,05.{t_1}} \right)}}{1}\\{x_N} = 82,5 = \dfrac{{{k_1}'.0,56.\left( {2,5 + 0,05.{t_1}} \right)}}{1}\end{array} \right. \Rightarrow \dfrac{{{x_M}}}{{{x_N}}} = \dfrac{{{k_1}}}{{{k_1}'}} = \dfrac{{107,25}}{{82,5}} = 1,3\\ \Rightarrow \left\{ \begin{array}{l}{k_1} = 65\\{k_1}' = 50\end{array} \right. \Rightarrow {t_1} = \dfrac{{125}}{{14}}\left( s \right)\end{array}\) + t2 là thời điểm đầu tiên mà tại M cho vân tối, đồng thời tại N cho vân sáng. Ta có: \(\begin{array}{l}\left\{ \begin{array}{l}{x_M} = 107,25 = \left( {{k_2} + \dfrac{1}{2}} \right).\dfrac{{0,56.\left( {2,5 + 0,05.{t_2}} \right)}}{1}\\{x_N} = 82,5 = {k_2}'.\dfrac{{0,56.\left( {2,5 + 0,05.{t_2}} \right)}}{1}\end{array} \right. \Rightarrow \dfrac{{{x_M}}}{{{x_N}}} = \dfrac{{{k_2} + \dfrac{1}{2}}}{{{k_2}'}} = \dfrac{{107,25}}{{82,5}} = 1,3\\ \Rightarrow \left\{ \begin{array}{l}{k_2} + \dfrac{1}{2} = 71,5\\{k_2}' = 55\end{array} \right. \Rightarrow {t_2} = \dfrac{{25}}{7}\left( s \right)\end{array}\) => Khoảng thời gian \(\Delta t = \left| {{t_1} - {t_2}} \right| = \left| {\dfrac{{125}}{{14}} - \dfrac{{25}}{7}} \right| = \dfrac{{75}}{{14}} = 5,357s\)
Câu 25 :
Tia hồng ngoại được dùng
Đáp án : B Phương pháp giải :
Tia hồng ngoại được dùng để: sấy khô, sưởi ấm; chụp ảnh hồng ngoại, điều khiển dùng hồng ngoại và dùng trong lĩnh vực quân sự. Lời giải chi tiết :
Tia hồng ngoại được dùng để chụp ảnh vào ban đêm |




















Danh sách bình luận