Đề kiểm tra 1 tiết chương 7: Hạt nhân nguyên tử - Đề số 2Đề bài
Câu 1 :
Bản chất lực tương tác giữa các nuclon trong hạt nhân là:
Câu 2 :
Điều kiện để xảy ra phản ứng dây truyền là?
Câu 3 :
Cho phản ứng hạt nhân \({}_1^3T + {}_Z^AX \to {}_2^4He + {}_0^1n\), hạt nhân X là hạt nhân nào sau đây?
Câu 4 :
Biểu thức xác định khối lượng hạt nhân đã phân rã trong thời gian t là:
Câu 5 :
Các nguyên tử nào sau đây là đồng vị:
Câu 6 :
Tính năng lượng tỏa ra khi tạo thành \(1g\) \(_2^4He\) từ các proton và notron. Cho biết độ hụt khối của hạt nhân \(He\) là \(∆m = 0,0304u\), \(1u = 931 (MeV/c^2)\); \(1MeV = 1,6.10^{-13}(J)\). Biết số Avôgađrô \(N_A = 6,02.10^{23} mol^{-1}\), khối lượng mol của \(_2^4He\) là \(4g/mol\)
Câu 7 :
Một prôtôn có động năng Kp = 1,5MeV bắn vào hạt nhân \({}_3^7Li\) đang đứng yên thì sinh ra 2 hạt X có bản chất giống nhau và không kèm theo bức xạ gamma. Tính động năng của mỗi hạt X? Cho mLi = 7,0144u; mp = 1,0073u; mX = 4,0015u; 1uc2 = 931MeV.
Câu 8 :
Cho ba hạt nhân X, Y và Z có số nuclon tương ứng là \({A_X},{\rm{ }}{A_Y},{\rm{ }}{A_Z}\) với \({A_X} = {\rm{ }}2{A_Y} = {\rm{ }}0,5{A_Z}\) . Biết năng lượng liên kết của từng hạt nhân tứng ứng là \(\Delta {E_X},\Delta {E_{Y,}}\Delta {E_Z}\) với \(\Delta {E_Z} < \Delta {E_X} < \Delta {E_Y}\) . Sắp xếp các hạt nhân này theo thứ tự tính bền vững giảm dần là:
Câu 9 :
Để thực hiện phản ứng nhiệt hạch, vì sao cần có điều kiện mật độ hạt nhân đủ lớn?
Câu 10 :
Trong quá trình phân rã, số hạt nhân phóng xạ
Câu 11 :
Cho phản ứng hạt nhân \(_0^1n + _3^6Li \to _1^3H + \alpha \). Hạt Li đứng yên, nơtron có động năng \(2MeV\). Hạt \(\alpha \) và hạt nhân H bay ra theo các hướng hợp với hướng tới của nơtron những góc tương ứng bằng \({15^0}\) và \({30^0}\). Bỏ qua búc xạ gamma. Lấy tỉ số khối lượng các hạt bằng tỉ số giữa các số khối của chúng. Phản ứng thu hay tỏa bao nhiêu năng lượng?
Câu 12 :
Dùng một proton có động năng \(5,45{\rm{ }}MeV\) bắn vào hạt nhân \(_4^9Be\) đang đứng yên. Phản ứng tạo ra hạt nhân \(X\) và hạt \(\alpha \). Hạt \(\alpha \) bay ra theo phương vuông góc với phương tới của hạt proton và có động năng \(4,0{\rm{ }}MeV\). Khi tính động năng của các hạt, lấy khối lượng các hạt nhân tính theo đơn vị khối lượng nguyên tử bằng số khối của chúng. Năng lượng tỏa ra trong phản ứng này bằng:
Câu 13 :
Chất phóng xạ pôlôni phát ra tia \(\alpha\) và biến đổi thành chì . Gọi chu kì bán rã của pôlôni là \(T\). Ban đầu \((t = 0)\) có một mẫu nguyên chất. Trong khoảng thời gian từ \(t = 0\) đến \(t = 2T\), có \(63 mg\) trong mẫu bị phân rã. Lấy khối lượng nguyên tử tính theo đơn vị \(u\) bằng số khối của hạt nhân của nguyên tử đó. Trong khoảng thời gian từ \(t = 2T \) đến \(t = 3T\), lượng chì được tạo thành trong mẫu có khối lượng là:
Câu 14 :
Nguyên tử được cấu tạo bởi:
Câu 15 :
Cho khối lượng nguyên tử của đồng vị Cacbon \({}_6^{13}C\); êlectron; prôtôn và nơtron lần lượt là \(12112,490{\rm{ }}MeV/{\rm{ }}{c^2}\) ; \(0,511{\rm{ }}MeV/{c^2}\); \(938,256{\rm{ }}MeV/{c^2}\) và \(939,550{\rm{ }}MeV/{c^2}\). Năng lượng liên kết của hạt nhân \({}_6^{13}C\) bằng:
Câu 16 :
Dùng một proton có động năng \(5,45 MeV\) bắn vào hạt nhân \({}_4^9Be\) đang đứng yên. Phản ứng tạo ra hạt nhân X và hạt \(α\). Hạt \(α\) bay ra theo phương vuông góc với phương tới của hạt proton và có động năng \(4,0 MeV\). Khi tính động năng của các hạt, lấy khối lượng các hạt nhân tính theo đơn vị khối lượng nguyên tử bằng số khối của chúng. Năng lượng tỏa ra trong phản ứng này bằng
Câu 17 :
Phản ứng hạt nhân \(_1^2H + _1^3H \to _2^4He + _0^1n\) tỏa ra năng lượng 17,6 MeV. Giả sử ban đầu động năng các hạt không đáng kể. Coi khối lượng các hạt nhân (theo u) xấp xỉ số khối của nó. Động năng của Heli là:
Câu 18 :
Hạt nhân \({}_{84}^{210}Po\) phân rã α thành hạt nhân con X. Số nuclon trong hạt nhân X bằng
Câu 19 :
Một chất phóng xạ có chu kì bán rã là 20 phút. Ban đầu một mẫu chất đó có khối lượng là 2g. Sau 1h40 phút, lượng chất đã phân rã là:
Câu 20 :
Khối lượng của hạt nhân \({}_4^9Be\) là 9,0027u, khối lượng của nơtron là mn = 1,0086u, khối lượng của prôtôn là mp = 1,0072u. Độ hụt khối của hạt nhân \({}_4^9Be\) là:
Câu 21 :
Biết năng lượng liên kết riêng của hạt nhân đơteri là 1,1MeV/nuclon và của hêli là 7MeV/nuclon. Khi hai hạt đơteri tổng hợp thành một nhân hêli (\({}_2^4He\)) năng lượng toả ra là
Câu 22 :
Điều nào sau đây là sai khi nói về phản ứng nhiệt hạch ?
Câu 23 :
Cho rằng khi một hạt nhân urani \(_{92}^{235}U\)phân hạch thì tỏa ra năng lượng trung bình là 200 MeV. Lấy NA = 6,023.1023 mol-1 , khối lượng mol của urani \(_{92}^{235}U\) là 235 g/mol. Năng lượng tỏa ra khi phân hạch hết 1 kg urani \(_{92}^{235}U\) là
Câu 24 :
Trong phòng thí nghiệm, người ta tiến hành xác định chu kì bán rã \(T\) của một chất phóng xạ bằng cách dùng máy đếm xung để đo tỉ lệ giữa số hạt bị phân rã \({\rm{\Delta N}}\) và số hạt ban đầu \({{\rm{N}}_{\rm{0}}}{\rm{.}}\) Dựa vào kết quả thực nghiệm đo được trên đồ thị hãy tính chu kì bán rã của chất phóng xạ này? 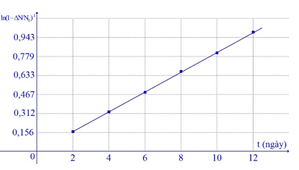
Câu 25 :
Nitơ tự nhiên có khối lượng nguyên tử là mN =14,0067u gồm hai đồng vị chính là N14 và N15 có khối lượng nguyên tử lần lượt là m14 =14,00307u và m15 =15,00011u. Tỉ lệ đồng vị N14 và N15 trong nitơ tự nhiên tương ứng bằng
Lời giải và đáp án
Câu 1 :
Bản chất lực tương tác giữa các nuclon trong hạt nhân là:
Đáp án : D Lời giải chi tiết :
Lực tương tác giữa các nuclon gọi là lực hạt nhân (tương tác hạt nhân hay tương tác mạnh)
Câu 2 :
Điều kiện để xảy ra phản ứng dây truyền là?
Đáp án : D Phương pháp giải :
Xem lí thuyết phần 1 Lời giải chi tiết :
Điều kiện để xảy ra phản ứng dây chuyền: xét số nơtrôn trung bình k sinh ra sau mỗi phản ứng phân hạch (\(k\) là hệ số nhân nơtron). + Nếu \(k < 1\): thì phản ứng dây chuyền không thể xảy ra. + Nếu \(k = 1\): thì phản ứng dây chuyền sẽ xảy ra và điều khiển được. + Nếu \(k > 1\): thì phản ứng dây chuyền xảy ra không điều khiển được.
Câu 3 :
Cho phản ứng hạt nhân \({}_1^3T + {}_Z^AX \to {}_2^4He + {}_0^1n\), hạt nhân X là hạt nhân nào sau đây?
Đáp án : A Lời giải chi tiết :
Áp dụng định luật bảo toàn điện tích và bảo toàn số khối ta xác định được : A = 2, Z = 1 => X là \(_1^2D\)
Câu 4 :
Biểu thức xác định khối lượng hạt nhân đã phân rã trong thời gian t là:
Đáp án : A Phương pháp giải :
Xem lại lí thuyết dạng 2 Lời giải chi tiết :
Khối lượng hạt nhân đã phân rã: \(\Delta m{\rm{ }} = {m_0}(1 - {2^{ - \frac{t}{T}}}) = {m_0}\left( {1 - {e^{ - \lambda t}}} \right)\)
Câu 5 :
Các nguyên tử nào sau đây là đồng vị:
Đáp án : A Lời giải chi tiết :
Đồng vị (cùng vị trí) là các nguyên tử giống nhau về số Z khác nhau về số A A - là đồng vị vì Z của 2 nguyên tử giống nhau B, C, D - không phải là đồng vị vì Z của các nguyên tử khác nhau
Câu 6 :
Tính năng lượng tỏa ra khi tạo thành \(1g\) \(_2^4He\) từ các proton và notron. Cho biết độ hụt khối của hạt nhân \(He\) là \(∆m = 0,0304u\), \(1u = 931 (MeV/c^2)\); \(1MeV = 1,6.10^{-13}(J)\). Biết số Avôgađrô \(N_A = 6,02.10^{23} mol^{-1}\), khối lượng mol của \(_2^4He\) là \(4g/mol\)
Đáp án : C Phương pháp giải :
Năng lượng tỏa ra khi tạo thành 1 hạt nhân: \(\Delta m{c^2}\) Lời giải chi tiết :
Ta có: + Năng lượng tỏa ra khi tạo thành 1 nguyên tử \(_2^4He\) từ các proton và nơtron: \(\Delta m{c^2}\) + \(1g\) \(_2^4He\) có số nguyên tử là: \(N = n.{N_A} = \dfrac{m}{M}{N_A} = \dfrac{1}{4}.6,{02.10^{23}} = 1,{505.10^{23}}\) + Năng lượng tỏa ra khi tạo thành \(1g\) \(_2^4He\) từ các proton và nơtron là: \(\begin{array}{l}Q = N.\Delta m{c^2} = 1,{505.10^{23}}.0,0304.931.{c^2}\\ = 4,{26.10^{24}}MeV = 4,{26.10^{24}}.1,6.10^{-13}=6,{82.10^{11}}J\end{array}\)
Câu 7 :
Một prôtôn có động năng Kp = 1,5MeV bắn vào hạt nhân \({}_3^7Li\) đang đứng yên thì sinh ra 2 hạt X có bản chất giống nhau và không kèm theo bức xạ gamma. Tính động năng của mỗi hạt X? Cho mLi = 7,0144u; mp = 1,0073u; mX = 4,0015u; 1uc2 = 931MeV.
Đáp án : A Phương pháp giải :
Năng lượng toả ra của phản ứng: ∆E = (mt – ms)c2 = Ks - Kt (mt, Kt lần lượt là tổng khối lượng và tổng động năng của những hạt trước phản ứng; ms, Ks lần lượt là tổng khối lượng và tổng động năng của những hạt sau phản ứng) Lời giải chi tiết :
Phương trình phản ứng: \(p + {}_3^7Li \to {}_2^4X + {}_2^4X\) Ta có năng lượng toả ra của phản ứng: ∆E = (mLi + mP - 2mX)c² = (7,0144 + 1,0073 – 2.4,0015).931 = 17,4097 MeV \(\Delta E = 2{K_\alpha } - {K_p} \to {K_\alpha } = \frac{{\Delta E + {K_p}}}{2} = 9,4549MeV\)
Câu 8 :
Cho ba hạt nhân X, Y và Z có số nuclon tương ứng là \({A_X},{\rm{ }}{A_Y},{\rm{ }}{A_Z}\) với \({A_X} = {\rm{ }}2{A_Y} = {\rm{ }}0,5{A_Z}\) . Biết năng lượng liên kết của từng hạt nhân tứng ứng là \(\Delta {E_X},\Delta {E_{Y,}}\Delta {E_Z}\) với \(\Delta {E_Z} < \Delta {E_X} < \Delta {E_Y}\) . Sắp xếp các hạt nhân này theo thứ tự tính bền vững giảm dần là:
Đáp án : A Lời giải chi tiết :
Ta có, năng lượng liên kết riêng của các hạt nhân là: \({\varepsilon _Y} = \dfrac{{\Delta {E_Y}}}{{{A_Y}}}\) \({\varepsilon _X} = \dfrac{{\Delta {E_X}}}{{{A_X}}} = \dfrac{{\Delta {E_X}}}{{2{A_Y}}} = \dfrac{{\Delta {E_X}}}{{2\Delta {E_Y}}}{\varepsilon _Y}\) \({\varepsilon _Z} = \dfrac{{\Delta {E_Z}}}{{{A_Z}}} = \dfrac{{\Delta {E_Z}}}{{4{A_Y}}} = \dfrac{{\Delta {E_Z}}}{{4\Delta {E_Y}}}{\varepsilon _Y}\) Theo đề bài, ta có: \(\Delta {E_Z} < \Delta {E_X} < \Delta {E_Y} \to {\varepsilon _Y} > {\varepsilon _X} > {\varepsilon _Z}\) => các hạt nhân được sắp xếp theo thứ tự giảm dần tính bền vững là: \(Y, X, Z\)
Câu 9 :
Để thực hiện phản ứng nhiệt hạch, vì sao cần có điều kiện mật độ hạt nhân đủ lớn?
Đáp án : D Phương pháp giải :
Vận dụng lí thuyết về phản ứng nhiệt hạch- phân hạch Lời giải chi tiết :
Để thực hiện phản ứng nhiệt hạch, cần có điều kiện mật độ hạt nhân đủ lớn để giảm khoảng cách hạt nhân tới bán kính tác dụng
Câu 10 :
Trong quá trình phân rã, số hạt nhân phóng xạ
Đáp án : B Phương pháp giải :
Vận dụng biểu thức tính số hạt nhân phóng xạ Lời giải chi tiết :
Ta có, số hạt nhân phóng xạ: \(N = {N_0}{2^{ - \frac{t}{T}}} = {N_0}.{e^{ - \lambda t}}\) => Số hạt nhân phóng xạ giảm theo thời gian theo định luật hàm số mũ
Câu 11 :
Cho phản ứng hạt nhân \(_0^1n + _3^6Li \to _1^3H + \alpha \). Hạt Li đứng yên, nơtron có động năng \(2MeV\). Hạt \(\alpha \) và hạt nhân H bay ra theo các hướng hợp với hướng tới của nơtron những góc tương ứng bằng \({15^0}\) và \({30^0}\). Bỏ qua búc xạ gamma. Lấy tỉ số khối lượng các hạt bằng tỉ số giữa các số khối của chúng. Phản ứng thu hay tỏa bao nhiêu năng lượng?
Đáp án : C Phương pháp giải :
Sử dụng định luật bảo toàn động lượng và định lý sin trong tam giác Lời giải chi tiết :
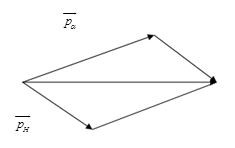
Phương trình phản ứng là: \(_0^1n + _3^6Li \to _1^3H + _2^4He\) Áp dụng định luật bảo toàn động lượng, ta vẽ được giản đồ vecto động lượng của phản ứng là:
Áp dụng định lý hàm số sin trong tam giác ta có: \(\begin{array}{l}\dfrac{{{p_n}}}{{\sin {{135}^0}}} = \dfrac{{{p_H}}}{{\sin {{15}^0}}} = \dfrac{{{p_\alpha }}}{{\sin {{30}^0}}}\\ = > \dfrac{{{p_H}}}{{{p_n}}} = \dfrac{{\sin {{15}^0}}}{{\sin {{135}^0}}} = > \dfrac{{{p_H}^2}}{{{p_n}^2}} = \dfrac{{{{\sin }^2}{{15}^0}}}{{{{\sin }^2}{{135}^0}}}\\ = > \dfrac{{{m_H}.{K_H}}}{{{m_n}.{K_n}}} = \dfrac{{{{\sin }^2}{{15}^0}}}{{{{\sin }^2}{{135}^0}}}\\ = > {K_H} = \dfrac{{1.2}}{3}.\dfrac{{{{\sin }^2}{{15}^0}}}{{{{\sin }^2}{{135}^0}}} = 0,089MeV\\\dfrac{{{p_{He}}}}{{{p_n}}} = \dfrac{{\sin {{30}^0}}}{{\sin {{135}^0}}} = > \dfrac{{{p_{He}}^2}}{{{p_n}^2}} = \dfrac{{{{\sin }^2}{{30}^0}}}{{{{\sin }^2}{{135}^0}}}\\ = > \dfrac{{{m_{He}}.{K_{He}}}}{{{m_n}.{K_n}}} = \dfrac{{{{\sin }^2}{{30}^0}}}{{{{\sin }^2}{{135}^0}}}\\ = > {K_{He}} = \dfrac{{1.2}}{4}.\dfrac{{{{\sin }^2}{{30}^0}}}{{{{\sin }^2}{{135}^0}}} = 0,25MeV\end{array}\) Năng lượng thu vào \(\Delta E = {K_{tr}} - {K_s} = 2 - 0,089 - 0,25 = 1,66MeV\)
Câu 12 :
Dùng một proton có động năng \(5,45{\rm{ }}MeV\) bắn vào hạt nhân \(_4^9Be\) đang đứng yên. Phản ứng tạo ra hạt nhân \(X\) và hạt \(\alpha \). Hạt \(\alpha \) bay ra theo phương vuông góc với phương tới của hạt proton và có động năng \(4,0{\rm{ }}MeV\). Khi tính động năng của các hạt, lấy khối lượng các hạt nhân tính theo đơn vị khối lượng nguyên tử bằng số khối của chúng. Năng lượng tỏa ra trong phản ứng này bằng:
Đáp án : B Phương pháp giải :
+ Sử dụng định luật bảo toàn số khối và bảo toàn điện tích để viết phương trình phản ứng. + Sử dụng định luật bảo toàn động lượng trong phản ứng hạt nhân. + Công thức liên hệ giữa động lượng và động năng: \({p^2} = {\rm{ }}2mK\) + Công thức tính năng lượng toả ra của phản ứng: \(\Delta E{\rm{ }} = {\rm{ }}\left( {{m_t}-{\rm{ }}{m_s}} \right){c^2} = {\rm{ }}{K_s} - {\rm{ }}{K_t}\) (Kt, Ks lần lượt là tổng động năng của các hạt trước và sau phản ứng) Lời giải chi tiết :
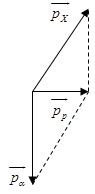
+ PT phản ứng: \(p + _4^9Be \to \alpha {\rm{ }} + _3^6X\) + Theo định luật bảo toàn động lượng ta có: \(\overrightarrow {{p_p}} {\rm{ }} = \overrightarrow {{p_\alpha }} {\rm{ }} + \overrightarrow {{p_X}} \) => ta biểu diễn bằng hình vẽ sau:
Từ hình vẽ ta có: \(p_X^2 = p_\alpha ^2 + p_p^2\) Mà : \({p^2} = 2mK \Rightarrow {m_X}{K_X} = {m_\alpha }{K_\alpha } + {m_p}{K_p} \Rightarrow {K_X} = \dfrac{{{m_\alpha }{K_\alpha } + {m_p}{K_p}}}{{{m_X}}} = \dfrac{{4.4 + 1.5,45}}{6} = 3,575(MeV)\) Năng lượng tỏa ra của phản ứng : \(\Delta E = {K_X} + {K_\alpha } - {K_p} = 3,575 + 4 - 5,45 = 2,125(MeV)\)
Câu 13 :
Chất phóng xạ pôlôni phát ra tia \(\alpha\) và biến đổi thành chì . Gọi chu kì bán rã của pôlôni là \(T\). Ban đầu \((t = 0)\) có một mẫu nguyên chất. Trong khoảng thời gian từ \(t = 0\) đến \(t = 2T\), có \(63 mg\) trong mẫu bị phân rã. Lấy khối lượng nguyên tử tính theo đơn vị \(u\) bằng số khối của hạt nhân của nguyên tử đó. Trong khoảng thời gian từ \(t = 2T \) đến \(t = 3T\), lượng chì được tạo thành trong mẫu có khối lượng là:
Đáp án : D Phương pháp giải :
Vận dụng biểu thức tính khối lượng chất phân rã: \(\Delta m = {m_0}\left( {1 - {2^{ - \dfrac{t}{T}}}} \right)\) Lời giải chi tiết :
\({m_o} - \dfrac{{{m_o}}}{{{2^2}}} = 63mg \to {m_o} = 84mg\) + Thời điểm \(t=2T\) ta có: \({m_o}^\prime = \dfrac{{{m_o}}}{4} = 21mg\) + Số hạt Po bị phân rã trong thời gian từ \(2T\) đến \(3T\) là: \(\begin{array}{l}\Delta N = \dfrac{{{m_0}'}}{{2.210}}.{N_A}\\ \to {m_{Pb}} = \dfrac{{\Delta N}}{{{N_A}}}{A_{Pb}} = \dfrac{{\dfrac{{{m_0}'}}{{2.210}}.{N_A}}}{{{N_A}}}.{A_{Pb}}\\ = \dfrac{{21}}{{2.210}}.206 = \dfrac{{103}}{{10}} = 10,3mg\end{array}\)
Câu 14 :
Nguyên tử được cấu tạo bởi:
Đáp án : A Lời giải chi tiết :
Nguyên tử được cấu tạo bởi các electron và hạt nhân. Hạt nhân nguyên tử tử cấu tạo bởi proton và nơtron => Nguyên tử cấu tạo bởi: electron, proton và notron
Câu 15 :
Cho khối lượng nguyên tử của đồng vị Cacbon \({}_6^{13}C\); êlectron; prôtôn và nơtron lần lượt là \(12112,490{\rm{ }}MeV/{\rm{ }}{c^2}\) ; \(0,511{\rm{ }}MeV/{c^2}\); \(938,256{\rm{ }}MeV/{c^2}\) và \(939,550{\rm{ }}MeV/{c^2}\). Năng lượng liên kết của hạt nhân \({}_6^{13}C\) bằng:
Đáp án : B Phương pháp giải :
Áp dụng công thức tính năng lượng liên kết \({{\rm{W}}_{lk}} = \Delta m{c^2} = \left( {Z{m_p} + \left( {A - Z} \right){m_n} - {m_O}} \right){c^2}\) Lời giải chi tiết :
\(\Delta E = \Delta m{c^2} = \left[ {Z{m_p} + \left( {A - Z} \right){m_n} - {m_X}} \right] = \left[ {Z{m_p} + \left( {A - Z} \right){m_n} - \left( {{m_{nt}} - Z{m_e}} \right)} \right]\) \(\Delta E = \left[ {6.938,256 + (13 - 6).939,550 - (12112,490 - 6.0,511)} \right]\frac{{MeV}}{{{c^2}}}{c^2} = 96,962MeV\) Chú ý
Học sinh chú ý đơn vị khối lượng của các hạt
Câu 16 :
Dùng một proton có động năng \(5,45 MeV\) bắn vào hạt nhân \({}_4^9Be\) đang đứng yên. Phản ứng tạo ra hạt nhân X và hạt \(α\). Hạt \(α\) bay ra theo phương vuông góc với phương tới của hạt proton và có động năng \(4,0 MeV\). Khi tính động năng của các hạt, lấy khối lượng các hạt nhân tính theo đơn vị khối lượng nguyên tử bằng số khối của chúng. Năng lượng tỏa ra trong phản ứng này bằng
Đáp án : B Phương pháp giải :
+ Sử dụng định luật bảo toàn số khối và bảo toàn điện tích để viết phương trình phản ứng. + Sử dụng định luật bảo toàn động lượng trong phản ứng hạt nhân. + Công thức liên hệ giữa động lượng và động năng: \({p^2} = {\rm{ }}2mK\) + Công thức tính năng lượng toả ra của phản ứng: \(\Delta E = \left( {{m_t} - {m_s}} \right){c^2} = {K_s} - {K_t}\) (Kt, Ks lần lượt là tổng động năng của các hạt trước và sau phản ứng) Lời giải chi tiết :
+ PT phản ứng: \(p + {}_4^9Be \to \alpha + {}_3^6X\) + Theo định luật bảo toàn động lượng ta có: \(\overrightarrow {{p_p}} = \overrightarrow {{p_\alpha }} + \overrightarrow {{p_X}} \) => ta biểu diễn bằng hình vẽ sau: 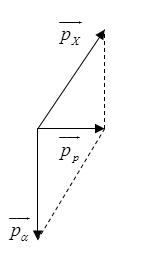 Từ hình vẽ ta có: \(p_X^2 = p_\alpha ^2 + p_p^2\) Mà : \({p^2} = 2mK \Rightarrow {m_X}{K_X} = {m_\alpha }{K_\alpha } + {m_p}{K_p} \Rightarrow {K_X} = \dfrac{{{m_\alpha }{K_\alpha } + {m_p}{K_p}}}{{{m_X}}} = \dfrac{{4.4 + 1.5,45}}{6} = 3,575(MeV)\) Năng lượng tỏa ra của phản ứng : \(\Delta E = {K_X} + {K_\alpha } - {K_p} = 3,575 + 4 - 5,45 = 2,125(MeV)\)
Câu 17 :
Phản ứng hạt nhân \(_1^2H + _1^3H \to _2^4He + _0^1n\) tỏa ra năng lượng 17,6 MeV. Giả sử ban đầu động năng các hạt không đáng kể. Coi khối lượng các hạt nhân (theo u) xấp xỉ số khối của nó. Động năng của Heli là:
Đáp án : D Phương pháp giải :
Áp dụng định luật bảo toàn động lượng và định luật bảo toàn năng lượng Lời giải chi tiết :
Ta có: \(\begin{array}{l}\overrightarrow 0 = {m_\alpha }\overrightarrow {{v_\alpha }} + {m_n}\overrightarrow {{v_n}} \to {m_\alpha }\overrightarrow {{v_\alpha }} = - {m_n}\overrightarrow {{v_n}} \\ \to {\left( {{m_\alpha }\overrightarrow {{v_\alpha }} } \right)^2} = {\left( { - {m_n}\overrightarrow {{v_n}} } \right)^2} \to {m_\alpha }{{\rm{W}}_\alpha } = {m_n}{{\rm{W}}_n}\\ \to {{\rm{W}}_\alpha } = \dfrac{1}{4}{{\rm{W}}_n}\end{array}\) Mặt khác: \(\Delta E = {{\rm{W}}_\alpha } + {{\rm{W}}_n} = \dfrac{1}{4}{{\rm{W}}_n} + {{\rm{W}}_n} \to {{\rm{W}}_n} = \dfrac{{17,6}}{{1,25}} = 14,08(MeV)\) => Động năng của Heli là: \({{\rm{W}}_\alpha } = \dfrac{1}{4}{{\rm{W}}_n} = \dfrac{{14,08}}{4} = 3,52MeV\)
Câu 18 :
Hạt nhân \({}_{84}^{210}Po\) phân rã α thành hạt nhân con X. Số nuclon trong hạt nhân X bằng
Đáp án : D Phương pháp giải :
+ Tia \(\alpha \) có bản chất là hạt nhân nguyên tử \({}_2^4He\) + Áp dụng định luật bảo toàn điện tích và số nuclon để viết phương trình phản ứng Lời giải chi tiết :
+ Ta có phương trình phóng xạ: \({}_{84}^{210}Po \to {}_2^4\alpha + {}_Z^AX\) + Áp dụng định luật bảo toàn số nuclon: 210 = 4 + A => A = 206
Câu 19 :
Một chất phóng xạ có chu kì bán rã là 20 phút. Ban đầu một mẫu chất đó có khối lượng là 2g. Sau 1h40 phút, lượng chất đã phân rã là:
Đáp án : A Phương pháp giải :
Áp dụng công thức tính khối lượng bị phân rã sau phản ứng \(\Delta m{\rm{ }} = {m_0}(1 - {2^{ - \dfrac{t}{T}}})\) Lời giải chi tiết :
Ta có: + Chu kì bán rã T = 20 phút + Thời gian t = 1h40 phút = 100 phút = 5T (T = 20 phút) + Khối lượng chất đã phân rã là : \(\Delta m = {m_0}.\left( {1 - {2^{ - \dfrac{t}{T}}}} \right) = 2.\left( {1 - {2^{ - \dfrac{{5T}}{T}}}} \right) = 2.\left( {1 - {2^{ - 5}}} \right) = 1,9375g\)
Câu 20 :
Khối lượng của hạt nhân \({}_4^9Be\) là 9,0027u, khối lượng của nơtron là mn = 1,0086u, khối lượng của prôtôn là mp = 1,0072u. Độ hụt khối của hạt nhân \({}_4^9Be\) là:
Đáp án : C Phương pháp giải :
Sử dụng công thức tính độ hụt khối: \(\Delta m = Z.{m_p} + N.{m_n} - {m_{hn}}\) Lời giải chi tiết :
Ta có, độ hụt khối \(\Delta m = Z.{m_p} + N.{m_n} - {m_{hn}}\) Lại có: \({}_4^9Be \to Z = 4;N = 9 - 4 = 5\) \( \to \Delta m = 4.1,0072 + 5.1,0086 - 9,0027 = 0,0691u\)
Câu 21 :
Biết năng lượng liên kết riêng của hạt nhân đơteri là 1,1MeV/nuclon và của hêli là 7MeV/nuclon. Khi hai hạt đơteri tổng hợp thành một nhân hêli (\({}_2^4He\)) năng lượng toả ra là
Đáp án : C Phương pháp giải :
Phương trình phản ứng hạt nhân: \(A + B \to C + D\) - Sử dụng công thức tính năng lượng phản ứng hạt nhân: \(\Delta E = {\varepsilon _C}.{A_C} + {\varepsilon _D}{A_D} - {\varepsilon _A}.{A_A} - {\varepsilon _B}.{A_B}\) Trong đó \(\varepsilon \) - năng lượng liên kết riêng
Lời giải chi tiết :
Ta có phản ứng hạt nhân: \({}_1^2D + {}_1^2D \to {}_2^4He\) \( \to \Delta E = {\varepsilon _{He}}.{A_{He}} - 2{\varepsilon _D}{A_D} = 7.4 - 2.1,1.2 = 23,6MeV\)
Câu 22 :
Điều nào sau đây là sai khi nói về phản ứng nhiệt hạch ?
Đáp án : D Phương pháp giải :
Sử dụng lí thuyết về phản ứng nhiệt hạch: là loại phản ứng tỏa năng lượng, xảy ra ở nhiệt độ rất cao (mặt trời, các ngôi sao…), dưới dạng không kiểm soát được Lời giải chi tiết :
A- đúng vì phản ứng nhiệt hạch là phản ứng tỏa năng lượng B- đúng vì điều kiện xảy ra phản ứng nhiệt hạch là ở nhiệt độ cao C- đúng vì phản ứng nhiệt hạch không kiểm soát được D- sai vì điều kiện xảy ra phản ứng nhiệt hạch là ở nhiệt độ cao
Câu 23 :
Cho rằng khi một hạt nhân urani \(_{92}^{235}U\)phân hạch thì tỏa ra năng lượng trung bình là 200 MeV. Lấy NA = 6,023.1023 mol-1 , khối lượng mol của urani \(_{92}^{235}U\) là 235 g/mol. Năng lượng tỏa ra khi phân hạch hết 1 kg urani \(_{92}^{235}U\) là
Đáp án : A Phương pháp giải :
+ Sử dụng biểu thức tính số hạt nhân: \(N = \dfrac{m}{M}{N_A}\) + Tính năng lượng tỏa ra khi phân hạch Lời giải chi tiết :
+ Số hạt nhân Urani trong 1kg: \(N = \dfrac{m}{M}{N_A} = \dfrac{{1000}}{{235}}.6,{023.10^{23}} = 25,{63.10^{24}}.\) + Năng lượng tỏa ra khi phân hạch hết \(1kg\) \({}_{92}^{235}U\)là: \(E = N.200 \approx 5,{13.10^{26}}(MeV)\)
Câu 24 :
Trong phòng thí nghiệm, người ta tiến hành xác định chu kì bán rã \(T\) của một chất phóng xạ bằng cách dùng máy đếm xung để đo tỉ lệ giữa số hạt bị phân rã \({\rm{\Delta N}}\) và số hạt ban đầu \({{\rm{N}}_{\rm{0}}}{\rm{.}}\) Dựa vào kết quả thực nghiệm đo được trên đồ thị hãy tính chu kì bán rã của chất phóng xạ này? 
Đáp án : B Phương pháp giải :
Áp dụng công thức tính số hạt còn lại trong mẫu sau thời gian t là: \(N = {N_0}{e^{ - \lambda t}} = {N_0}{2^{\dfrac{{ - t}}{T}}}\) Lời giải chi tiết :
Ta có: \(N = {N_0}{e^{ - \lambda t}} \Rightarrow \)Số hạt bị phân rã là: \(\Delta N = {N_0} - {N_0}{e^{ - \lambda t}} = {N_0}(1 - {e^{ - \lambda t}})\) \( \Rightarrow \dfrac{{\Delta N}}{{{N_0}}} = 1 - {e^{ - \lambda t}} \Rightarrow 1 - \dfrac{{\Delta N}}{{{N_0}}} = {e^{ - \lambda t}}\) \( \Rightarrow \dfrac{1}{{\left( {1 - \dfrac{{\Delta N}}{{{N_0}}}} \right)}} = {e^{\lambda t}} \Rightarrow \ln {\left( {1 - \dfrac{{\Delta N}}{{{N_0}}}} \right)^{ - 1}} = \lambda t\) Từ đồ thị ta thấy \(\lambda \approx 0,078\) \( \Rightarrow T = \dfrac{{\ln 2}}{\lambda } \approx 8,9\) (ngày)
Câu 25 :
Nitơ tự nhiên có khối lượng nguyên tử là mN =14,0067u gồm hai đồng vị chính là N14 và N15 có khối lượng nguyên tử lần lượt là m14 =14,00307u và m15 =15,00011u. Tỉ lệ đồng vị N14 và N15 trong nitơ tự nhiên tương ứng bằng
Đáp án : C Phương pháp giải :
Khối lượng nguyên tử khối trung bình: \({m_N} = \dfrac{{{m_{{N_{14}}}}.{n_{{N_{14}}}} + {m_{{N_{15}}}}.{n_{{N_{15}}}}}}{{{n_{{N_{14}}}} + {n_{{N_{15}}}}}}\) Lời giải chi tiết :
+ Trong 100 hạt N tự nhiên thì có x hạt N14 và y = (100-x) hạt N15. Ta có: \(x.{m_{{N_{14}}}} + (100 - x){m_{{N_{15}}}} = 100{m_N} \to \)\(x \approx 99,6359;y \approx 0,3641\) |




















Danh sách bình luận