Đề kiểm tra học kì 2 - Đề số 1Đề bài
Câu 1 :
Hạt nhân nguyên tử cấu tạo bởi:
Câu 2 :
Phát biểu nào sau đây là đúng?
Câu 3 :
Hiện tượng phóng xạ là
Câu 4 :
Ánh sáng trên bề mặt rộng 7,2 mm của vùng giao thoa người ta đếm được 9 vân sáng (hai rìa là hai vân sáng). Tại vị trí cách vân trung tâm 14,4 mm ℓà vân:
Câu 5 :
Trong thí nghiệm I-âng về giao thoa ánh sáng, hai khe được chiếu sáng đồng thời bởi hai bức xạ đơn sắc có bước sóng lần lượt là \({\lambda _1}\) và \({\lambda _2}\). Trên màn quan sát có vân sáng bậc 12 của \({\lambda _1}\) trùng với vân sáng bậc 10 của \({\lambda _2}\). Tỉ số \(\frac{{{\lambda _1}}}{{{\lambda _2}}}\) bằng:
Câu 6 :
Tìm phát biểu sai. Dao động điện từ trong mạch dao động LC bị tắt dần là do:
Câu 7 :
Mạch dao động điện từ gồm tụ điện C và cuộn cảm L, dao động tự do với tần số góc
Câu 8 :
Thông tin nào sau đây là sai khi nói về các định luật bảo toàn trong phản ứng hạt nhân?
Câu 9 :
Ánh sáng đơn sắc là:
Câu 10 :
Sóng điện từ
Câu 11 :
Trong hiện tượng quang - phát quang, sự hấp thụ hoàn toàn một photon sẽ đưa đến:
Câu 12 :
Trong thí nghiệm giao thoa ánh sáng đơn sắc với hai khe I-âng, cho D=1,5m. Nguồn sáng S phát ra ánh sáng đơn sắc có bước sóng λ. Khoảng cách từ S đến mặt phẳng hai khe là d=60cm. Khoảng vân đo được trên màn bằng i=3mm. Cho S dời theo phương song song với S1S2 về phía S2. Để cường độ sáng tại O chuyển từ cực đại sang cực tiểu thì S phải dịch chuyển một đoạn tối thiểu bằng bao nhiêu?
Câu 13 :
Giới hạn quang điện của mỗi kim loại là:
Câu 14 :
Xét nguyên tử hiđrô theo mẫu nguyên tử Bo, trong các quỹ đạo dừng của êlectron có hai quỹ đạo có bán kính rmvà rn. Biết rm− rn= 36r0, trong đó r0 là bán kính Bo. Giá trị rm gần nhất với giá trị nào sau đây?
Câu 15 :
Khi nói về tia hồng ngoại và tia tử ngoại, phát biểu nào sau đây là đúng?
Câu 16 :
Một nguồn sáng S phát ra ánh sáng đơn sắc có bước sóng λ= 0,5 μm, đến khe Yâng S1, S2 với S1S2 = 0,5mm. Mặt phẳng chứa S1S2 cách màn D = 1m. Chiều rộng vùng giao thoa quan sát được L = 13mm. Tìm số vân sáng và vân tối quan sát được?
Câu 17 :
Trong thí nghiệm I-âng về giao thoa ánh sáng đơn sắc, khoảng vân sẽ:
Câu 18 :
Năng lượng liên kết của \(_{10}^{20}Ne\) là $160,64 MeV$. Biết khối lượng của proton là $1,007825u$ và khối lượng của notron là $1,00866u$. Coi $1u = 931,5MeV/{c^2}$. Khối lượng nguyên tử ứng với hạt nhân \(_{10}^{20}Ne\) là:
Câu 19 :
Trong thông tin liên lạc bằng sóng điện từ, sau khi trộn tín hiệu âm tần có tần số fa với tín hiệu dao động cao tần có tần số f ( biến điệu biên độ) thì tín hiệu đưa đến ăng ten phát biến thiên tuần hoàn với tần số
Câu 20 :
Ưu điểm nổi bật của đèn laze so với các loại đèn thông thường
Câu 21 :
Phát biểu nào sau đây là đúng khi nói về quang phổ?
Câu 22 :
Cho phản ứng hạt nhân: \(_{\rm{1}}^{\rm{2}}{\rm{D}} + _{\rm{1}}^{\rm{3}}{\rm{T}} \to _{\rm{2}}^{\rm{4}}{\rm{He}} + _{\rm{0}}^{\rm{1}}{\rm{n}}\). Biết năng lượng liên kết riêng của các hạt nhân tương ứng là: εD = 1,11 MeV/nuclôn, εT = 2,83 MeV/nuclôn, εHe = 7,10 MeV/nuclôn. Năng lượng tỏa ra của phản ứng hạt nhân này là
Câu 23 :
Mạch chọn sóng của một máy thu vô tuyến điện gồm một tụ điện có điện dung thay đổi từ \(\frac{{10}}{\pi }pF\) đến \(\frac{{160}}{\pi }pF\) và cuộn dây có độ tự cảm \(\frac{{2,5}}{\pi }\mu H\). Mạch trên có thể bắt được sóng điện từ có bước sóng nằm trong khoảng nào ?
Câu 24 :
Trong thí nghiệm Young về giao thoa ánh sáng, nếu sử dụng ánh sáng trắng có bước sóng 400nm đến 750nm. Tại vị trí của vân sáng bậc 3 của ánh sáng tím bước sóng 400nm còn có vân sáng của ánh sáng đơn sắc có bước sóng
Câu 25 :
Trong một thí nghiệm Y-âng về giao thoa ánh sáng, bước sóng ánh sáng đơn sắc là 600nm, khoảng cách giữa hai khe hẹp là 1mm. Khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là 2m. Khoảng vân quan sát trên mà có giá trị bằng:
Câu 26 :
Cường độ dòng điện tức thời trong mạch dao động LC có dạng $i= 0,02cos2000t(A)$. Tụ điện trong mạch có điện dung $5μF$. Độ tự cảm của cuộn cảm là:
Câu 27 :
Cho phản ứng \(_1^2D + _1^2D \to _2^3He + n + 3,25MeV\). Phản ứng này là:
Câu 28 :
Giả sử các electron đến được anốt của tế bào quang điện đều bị hút về anốt, khi đó dòng quang điện có cường độ I = 0,32mA. Số electron thoát ra khỏi catốt trong mỗi giây là:
Câu 29 :
Dùng chùm proton bắn phá hạt nhân \(_3^7Li\) đang đứng yên tạo ra 2 hạt nhân X giống nhau có cùng động năng là \(W\) nhưng bay theo hai hướng hợp với nhau một góc \(\varphi \) và không sinh ra tia gamma. Biết tổng năng lượng nghỉ của các hạt trước phản ứng chuyển nhiều hơn tổng năng lượng nghỉ của các hạt tạo thành là \(2W/3\). Coi khối lượng hạt nhân đo bằng đơn bị khối lượng nguyên tử gần bằng số khối của nó thì:
Câu 30 :
Cho mạch điện như hình vẽ, nguồn có suất điện động E=12V điện trở trong r = 1Ω, tụ có điện dung C=100μF, cuộn dây có hệ số tự cảm L=0,2H và điện trở là R0= 5Ω; điện trở R=18Ω. Ban đầu K đóng, khi trạng thái trong mạch đã ổn định người ta ngắt khoá K. Tính nhiệt lượng tỏa ra trên điện trở R trong thời gian từ khi ngắt K đến khi dao động trong mạch tắt hoàn toàn? 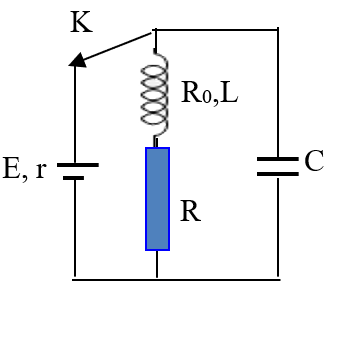
Câu 31 :
Người ta dùng một Laze hoạt động dưới chế độ liên tục để khoan một tấm thép. Công suất của chùm laze là P = 10 W, đường kính của chùm sáng là 1 mm. Bề dày tấm thép là e = 2 mm và nhiệt độ ban đầu là 300C. Biết khối lượng riêng của thép D = 7800 kg/m3 ; Nhiệt dung riêng của thép c = 448 J/kg.độ ; nhiệt nóng chảy của thép L = 270 kJ/kg và điểm nóng chảy của thép tc = 15350C. Thời gian khoan thép là
Câu 32 :
Cho khối lượng của hạt nhân \({}_2^4He\); prôtôn và nơtron lần lượt là 4,0015 u; 1,0073 u và 1,0087 u.Lấy 1 u = 1,66.10–27 kg; c = 3.108 m/s; NA = 6,02.1023 mol–1. Năng lượng tỏa ra khi tạo thành 1 mol \({}_2^4He\) từ các nuclôn là
Câu 33 :
Khi điện tích trên tụ tăng từ $0$ lên $0,5{\rm{ }}\left( {\mu C} \right)$ thì đồng thời cường độ dòng điện trong mạch dao động LC lí tưởng giảm từ $3\pi \left( {mA} \right)$ xuống \(\dfrac{{3\sqrt 3 \pi }}{2}mA\) . Khoảng thời gian xảy ra sự biến thiên này là:
Câu 34 :
Một anten parabol, đặt tại một điểm A trên mặt đất, phát ra một sóng truyền theo phương làm với mặt phẳng ngang góc 450 hướng lên một vệ tinh địa tĩnh V. Coi trái đất là hình cầu, bán kính R=6380km. Vệ tinh địa tĩnh ở độ cao 35800km so với mặt đất. Sóng này truyền từ A đến V mất thời gian:
Câu 35 :
Biết số Avôgađrô NA = 6,02.1023 hạt/mol và khối lượng của hạt nhân bằng số khối của nó. Số protôn có trong 0,27 gam \(_{13}^{^{27}}Al\) là
Câu 36 :
Trong thí nghiệm Y-âng về giao thoa của ánh sáng đơn sắc, hai khe hẹp cách nhau \(1 mm\), mặt phẳng chứa hai khe cách màn quan sát \(1,5 m\). Khoảng cách giữa \(5\) vân sáng liên tiếp là \(3,6 mm\). Bước sóng của ánh sáng dùng trong thí nghiệm này bằng:
Câu 37 :
Cho phản ứng phân hạch của Urani 235: \({}_{92}^{235}U + {}_0^1n \to {}_{42}^{95}Mo + {}_{57}^{139}La + 2{}_0^1n\). Biết khối lượng các hạt nhân: mU = 234,99u; mMo = 94,88u; mLa = 138,87u; mn = 1,0087u. Hỏi năng lượng tỏa ra khi 1 gam U phân hạch hết sẽ tương đương với năng lượng sinh ra khi đốt cháy bao nhiêu kg xăng? Biết rằng mỗi kg xăng cháy hết tỏa năng lượng 46.106 J.
Câu 38 :
Hiện nay trong quặng thiên nhiên có chứa cả \(_{92}^{238}U\) và \(_{92}^{235}U\) theo tỉ lệ nguyên tử là 140 :1. Giả sử ở thời điểm tạo thành Trái Đất, tỷ lệ trên là 1:1. Hãy tính tuổi của Trái Đất. Biết chu kỳ bán rã của \(_{92}^{238}U\) là 4,5.109 năm, \(_{92}^{235}U\) có chu kỳ bán rã 7,13.108 năm.
Câu 39 :
Một nguyên tử chuyển từ trạng thái dừng Em sang trạng thái dừng En (Em < En) khi hấp thụ một photon có năng lượng hf. Chọn câu đúng:
Câu 40 :
Một tụ điện có điện dung C được nạp điện tới điện tích q. Khi nối tụ với cuộn cảm thuần có độ tự cảm L1 thì trong mạch có dao động điện từ riêng với cường độ dòng điện cực đại bằng 70mA. Khi nối tụ với cuộn cảm thuần có độ tự cảm L2 thì trong mạch có dao động điện từ riêng với cường độ dòng điện cực dại bằng 35mA. Nếu nối tụ với cuộn cảm thuần có độ tự cảm ${L_3} = 13{L_1} + 9{L_2}$ thì trong mạch có cường độ dòng điện cực đại bằng
Lời giải và đáp án
Câu 1 :
Hạt nhân nguyên tử cấu tạo bởi:
Đáp án : C Lời giải chi tiết :
Hạt nhân nguyên tử cấu tạo bởi proton và nơtron, hai loại hạt này có tên chung là nuclôn
Câu 2 :
Phát biểu nào sau đây là đúng?
Đáp án : C Lời giải chi tiết :
Hiện tượng quang điện trong là hiện tượng electron liên kết được giải phóng thành êlectron dẫn khi chất bán dẫn được chiếu bằng bức xạ thích hợp.
Câu 3 :
Hiện tượng phóng xạ là
Đáp án : C Phương pháp giải :
Xem lí thuyết phần 1 Lời giải chi tiết :
Phóng xạ là hiện tượng hạt nhân không bền vững tự phân rã, phát ra các tia phóng xạ và biến đổi thành các hạt nhân khác.
Câu 4 :
Ánh sáng trên bề mặt rộng 7,2 mm của vùng giao thoa người ta đếm được 9 vân sáng (hai rìa là hai vân sáng). Tại vị trí cách vân trung tâm 14,4 mm ℓà vân:
Đáp án : D Phương pháp giải :
+ Áp dụng biểu thức tính khoảng cách giữa N vân sáng liên tiếp là (N-1)i + Áp dụng biểu thức xác định tính chất, vị trí vân sáng - tối Lời giải chi tiết :
Ta có, trên màn có 9 vân sáng => Khoảng cách giữa 9 vân sáng là 8i = 7,2mm => i = 0,9mm Tại vị trí cách trung tâm 14,4mm = 16i => Vân sáng thứ 16
Câu 5 :
Trong thí nghiệm I-âng về giao thoa ánh sáng, hai khe được chiếu sáng đồng thời bởi hai bức xạ đơn sắc có bước sóng lần lượt là \({\lambda _1}\) và \({\lambda _2}\). Trên màn quan sát có vân sáng bậc 12 của \({\lambda _1}\) trùng với vân sáng bậc 10 của \({\lambda _2}\). Tỉ số \(\frac{{{\lambda _1}}}{{{\lambda _2}}}\) bằng:
Đáp án : C Phương pháp giải :
Sử dụng công thức hai vân trùng nhau: x1 = x2 Vị trí vân sáng: xs = kλD/a = ki Lời giải chi tiết :
Tại vị trí vân trùng ta có:\(12{i_1} = 10{i_2} \Leftrightarrow 12{\lambda _1} = 10{\lambda _2} \Rightarrow \frac{{{\lambda _1}}}{{{\lambda _2}}} = \frac{5}{6}\)
Câu 6 :
Tìm phát biểu sai. Dao động điện từ trong mạch dao động LC bị tắt dần là do:
Đáp án : D Lời giải chi tiết :
A, B, C - đúng Mạch dao động điện từ tự do (mạch dao động LC lí tưởng) có năng lượng điện trường tập trung trong tụ điện và năng lượng từ trường tập trung trong cuộn cảm. Hai năng lượng này luôn chuyển hóa lẫn nhau => Sự chuyển hóa năng lượng điện trường sang từ trường và ngược lại không là nguyên nhân gây tắt dần dao động => D - sai
Câu 7 :
Mạch dao động điện từ gồm tụ điện C và cuộn cảm L, dao động tự do với tần số góc
Đáp án : D Phương pháp giải :
Xem lí thuyết mục 1- phần I - Bài Mạch dao động LC Lời giải chi tiết :
Tần số góc của dao động điện từ tự do được xác định bằng biểu thức: \(\omega = \frac{1}{{\sqrt {LC} }}\)
Câu 8 :
Thông tin nào sau đây là sai khi nói về các định luật bảo toàn trong phản ứng hạt nhân?
Đáp án : B Phương pháp giải :
Xem lí thuyết phần 2 Lời giải chi tiết :
A, C, D - đúng B - sai vì không có định luật bảo toàn số proton
Câu 9 :
Ánh sáng đơn sắc là:
Đáp án : D Lời giải chi tiết :
Ánh sáng đơn sắc là ánh sáng không bị tán sắc khi đi qua lăng kính
Câu 10 :
Sóng điện từ
Đáp án : B Phương pháp giải :
Xem lí thuyết mục 2- phần II Lời giải chi tiết :
Sóng điện từ là điện từ trường lan truyền trong không gian.
Câu 11 :
Trong hiện tượng quang - phát quang, sự hấp thụ hoàn toàn một photon sẽ đưa đến:
Đáp án : D Lời giải chi tiết :
Ta có: Hiện tượng quang - phát quang là hiện tượng chất phát quang có thể hấp thụ ánh sáng có bước sóng này để phát ra ánh sáng có bước sóng khác => Trong hiện tượng quang - phát quang, sự hấp thụ hoàn toàn một photon sẽ đưa đến sự phát ra một photon khác
Câu 12 :
Trong thí nghiệm giao thoa ánh sáng đơn sắc với hai khe I-âng, cho D=1,5m. Nguồn sáng S phát ra ánh sáng đơn sắc có bước sóng λ. Khoảng cách từ S đến mặt phẳng hai khe là d=60cm. Khoảng vân đo được trên màn bằng i=3mm. Cho S dời theo phương song song với S1S2 về phía S2. Để cường độ sáng tại O chuyển từ cực đại sang cực tiểu thì S phải dịch chuyển một đoạn tối thiểu bằng bao nhiêu?
Đáp án : C Phương pháp giải :
+ Vận dụng công thức khi dịch chuyển nguồn sáng (xem lí thuyết phần 1) + Sử dụng biểu thức vị trí vân sáng - tối Lời giải chi tiết :
Ta có, khi dịch chuyển nguồn sáng S theo phương song song về phía S2 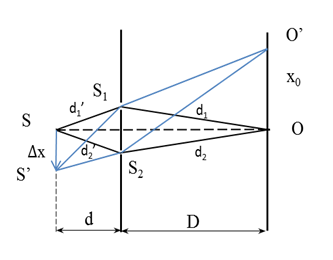 Khi đó, vân trung tâm dịch chuyển một đoạn \({x_0} = \frac{{\Delta xD}}{d}\) về phía S1 Ta có: \(OO' = {x_0}\), để tại O chuyển từ cực đại sang cực tiểu thì \({x_0} = (k + \frac{1}{2})i\) \( \leftrightarrow \frac{{\Delta xD}}{d} = \left( {k + \frac{1}{2}} \right)i \to \Delta x = \left( {k + \frac{1}{2}} \right)\frac{d}{D}i\) \({\left( {\Delta x} \right)_{\min }} = \frac{1}{2}\frac{d}{D}i\) (khi k = 0) Vậy để O chuyển từ cực đại sang cực tiểu thì S phải dịch chuyển một đoạn tối thiểu: \({\left( {\Delta x} \right)_{\min }} = \frac{1}{2}\frac{d}{D}i = \frac{1}{2}\frac{{0,6}}{{1,5}}{.3.10^{ - 3}} = 0,{6.10^{ - 3}}m = 0,6mm\)
Câu 13 :
Giới hạn quang điện của mỗi kim loại là:
Đáp án : A Lời giải chi tiết :
Ta có, điều kiện xảy ra hiện tượng quang điện là các bước sóng chiếu vào phải nhỏ hơn hoặc bằng giới hạn quang điện => Giới hạn quang điện \({\lambda _0}\) là bước sóng dài nhất của bức xạ chiếu vào kim loại đó mà gây ra được hiện tượng quang điện
Câu 14 :
Xét nguyên tử hiđrô theo mẫu nguyên tử Bo, trong các quỹ đạo dừng của êlectron có hai quỹ đạo có bán kính rmvà rn. Biết rm− rn= 36r0, trong đó r0 là bán kính Bo. Giá trị rm gần nhất với giá trị nào sau đây?
Đáp án : A Phương pháp giải :
Áp dụng công thức tính bán kính quỹ đạo ở trạng thái dừng n: rn = n2.r0 kết hợp suy luận toán học Lời giải chi tiết :
Theo bài ra ta có: \(\begin{array}{l}{r_m} = {m^2}{r_0}\left( {m \in {N^*}} \right);{r_n} = {n^2}{r_0}\left( {n \in {N^*}} \right)\\ \Rightarrow {r_m} - {r_n} = 36{r_0} \Rightarrow {m^2} - {n^2} = 36 \Rightarrow \left( {m - n} \right)\left( {m + n} \right) = 36\end{array}\) m – n và m + n là ước của 36. Mặt khác tổng của m – n và m + n là một số chẵn nên hai số m – n và m + n sẽ cùng chẵn hoặc cùng lẻ \( \Rightarrow \left\{ \begin{array}{l}m - n = 2\\m + n = 18\end{array} \right. \Rightarrow \left\{ \begin{array}{l}m = 10\\n = 8\end{array} \right. \Rightarrow {r_m} = 100{r_0}\)
Câu 15 :
Khi nói về tia hồng ngoại và tia tử ngoại, phát biểu nào sau đây là đúng?
Đáp án : B Phương pháp giải :
Sử dụng lí thuyết về tia hồng ngoại và tia tử ngoại (Xem lí thuyết phần 1) Lời giải chi tiết :
ta có:  => Bước sóng của tia hồng ngoại lớn hơn bước sóng của tia tử ngoại.
Câu 16 :
Một nguồn sáng S phát ra ánh sáng đơn sắc có bước sóng λ= 0,5 μm, đến khe Yâng S1, S2 với S1S2 = 0,5mm. Mặt phẳng chứa S1S2 cách màn D = 1m. Chiều rộng vùng giao thoa quan sát được L = 13mm. Tìm số vân sáng và vân tối quan sát được?
Đáp án : A Phương pháp giải :
+ Áp dụng công thức tính khoảng vân: \(i = \frac{{\lambda D}}{a}\) + Áp dụng công thức tính số vân sáng trên màn: \({N_S} = 2\left[ {\frac{L}{{2i}}} \right] + 1 = 13\) + Áp dụng biểu thức tính số vân tối trên màn Lời giải chi tiết :
Ta có: + Khoảng vân i: \(i = \frac{{\lambda D}}{a} = \frac{{0,{{5.10}^{ - 6}}.1}}{{0,{{5.10}^{ - 3}}}} = {10^{ - 3}}m = 1mm\) + Số vân sáng trên màn: \({N_S} = 2\left[ {\frac{L}{{2i}}} \right] + 1 = 13\) Ta có: phần thập phân của \(\frac{L}{{2i}} = 0,5\)=> Số vân tối trên màn: Nt = NS + 1 = 14
Câu 17 :
Trong thí nghiệm I-âng về giao thoa ánh sáng đơn sắc, khoảng vân sẽ:
Đáp án : B Phương pháp giải :
Công thức tính khoảng vân: i = λD/a Lời giải chi tiết :
Ta có: \(i = \frac{{\lambda D}}{a}\) => Khi a tăng thì i giảm.
Câu 18 :
Năng lượng liên kết của \(_{10}^{20}Ne\) là $160,64 MeV$. Biết khối lượng của proton là $1,007825u$ và khối lượng của notron là $1,00866u$. Coi $1u = 931,5MeV/{c^2}$. Khối lượng nguyên tử ứng với hạt nhân \(_{10}^{20}Ne\) là:
Đáp án : B Phương pháp giải :
Vận dụng biểu thức tính năng lượng liên kết \({{\rm{W}}_{lk}} = \left[ {Z{m_p} + \left( {A - Z} \right){m_n} - {m_X}} \right]{c^2}\) Lời giải chi tiết :
Ta có: \(\begin{array}{l}{{\rm{W}}_{lk}} = \left[ {Z{m_p} + \left( {A - Z} \right){m_n} - {m_{Ne}}} \right]{c^2} = 160,64MeV\\ = \left[ {10.1,007825u + (20 - 10).1,00866u - {m_{Ne}}} \right].{c^2}\\ \leftrightarrow (20,16485u - {m_{Ne}}){c^2} = \frac{{160,64}}{{931,5}}u{c^2}\\ \to {m_{Ne}} = 19,99239697u\end{array}\) Chú ý
Năng lượng tỏa ra khi tạo thành một hạt nhân X từ các proton và các nơtron bằng năng lượng liên kết. Năng lượng tỏa ra khi tạo thành n hạt nhân X từ các proton và notron : \(Q = n{{\rm{W}}_{lk}}\)
Câu 19 :
Trong thông tin liên lạc bằng sóng điện từ, sau khi trộn tín hiệu âm tần có tần số fa với tín hiệu dao động cao tần có tần số f ( biến điệu biên độ) thì tín hiệu đưa đến ăng ten phát biến thiên tuần hoàn với tần số
Đáp án : B Phương pháp giải :
Vận dụng lí thuyết về mạch biến điệu Lời giải chi tiết :
Trong thông tin liên lạc bằng sóng điện từ, sau khi trộn tín hiệu âm tần có tần số fa với tín hiệu dao động cao tần có tần số f ( biến điệu biên độ) thì tín hiệu đưa đến ăng ten phát biến thiên tuần hoàn với tần số f và biên độ biến thiên theo thời gian và tần số bằng fa.
Câu 20 :
Ưu điểm nổi bật của đèn laze so với các loại đèn thông thường
Đáp án : C Phương pháp giải :
Vận dụng lí thuyết về laze Lời giải chi tiết :
Dựa vào các đặc điểm của laze:
Câu 21 :
Phát biểu nào sau đây là đúng khi nói về quang phổ?
Đáp án : B Phương pháp giải :
Vận dụng lí thuyết về các loại quang phổ Lời giải chi tiết :
A - sai vì quang phổ liên tục không phụ thuộc vào thành phần cấu tạo của nguồn sáng B - đúng C - sai vì để thu được quang phổ vạch hấp thụ thì nhiệt độ của đám khí hay hơi hấp thụ phải thấp hơn nhiệt độ của nguồn sáng phát ra quang phổ liên tục D - sai vì quang phổ vạch hấp thụ là quang phổ của ánh sáng do khi chiếu ánh sáng trắng qua nguồn khí hay hơi có nhiệt độ thấp hơn của nguồn
Câu 22 :
Cho phản ứng hạt nhân: \(_{\rm{1}}^{\rm{2}}{\rm{D}} + _{\rm{1}}^{\rm{3}}{\rm{T}} \to _{\rm{2}}^{\rm{4}}{\rm{He}} + _{\rm{0}}^{\rm{1}}{\rm{n}}\). Biết năng lượng liên kết riêng của các hạt nhân tương ứng là: εD = 1,11 MeV/nuclôn, εT = 2,83 MeV/nuclôn, εHe = 7,10 MeV/nuclôn. Năng lượng tỏa ra của phản ứng hạt nhân này là
Đáp án : A Phương pháp giải :
Công thức tính năng lượng toả ra của phản ứng: ∆E = Wlks – Wlkt (Wlkt; Wlks lần lượt là tổng năng lượng liên kết của các hạt trước và sau phản ứng) Công thức liên hệ giữa năng lượng liên kết và năng lượng liên kết riêng ε là: Wlk = A.ε Lời giải chi tiết :
Năng lượng toả ra của phản ứng hạt nhân: \(\Delta {\rm{E}} = {{\rm{W}}_{lkHe}}{\rm{ - }}{{\rm{W}}_{lkD}}{\rm{ - }}{{\rm{W}}_{lkT}}{\rm{ = (4}}{{\rm{\varepsilon }}_{{\rm{He}}}} - {\rm{3}}{{\rm{\varepsilon }}_{\rm{T}}} - {\rm{2}}{{\rm{\varepsilon }}_{\rm{D}}}{\rm{)}} = {\rm{17,69MeV}}\)
Câu 23 :
Mạch chọn sóng của một máy thu vô tuyến điện gồm một tụ điện có điện dung thay đổi từ \(\frac{{10}}{\pi }pF\) đến \(\frac{{160}}{\pi }pF\) và cuộn dây có độ tự cảm \(\frac{{2,5}}{\pi }\mu H\). Mạch trên có thể bắt được sóng điện từ có bước sóng nằm trong khoảng nào ?
Đáp án : B Phương pháp giải :
Áp dụng biểu thức tính bước sóng: \(\lambda = 2\pi c\sqrt {LC} \) Lời giải chi tiết :
Ta có: \(\lambda = 2\pi c\sqrt {LC} \) + \({\lambda _{\min }} = 2\pi c\sqrt {L{C_{\min }}} = 2\pi {.3.10^8}\sqrt {\frac{{{{2,5.10}^{ - 6}}}}{\pi }.\frac{{{{10.10}^{ - 12}}}}{\pi }} = 3m\) + \({\lambda _{{\rm{max}}}} = 2\pi c\sqrt {L{C_{{\rm{max}}}}} = 2\pi {.3.10^8}\sqrt {\frac{{{{2,5.10}^{ - 6}}}}{\pi }.\frac{{{{160.10}^{ - 12}}}}{\pi }} = 12m\) \( \to 3m \le \lambda \le 12m\)
Câu 24 :
Trong thí nghiệm Young về giao thoa ánh sáng, nếu sử dụng ánh sáng trắng có bước sóng 400nm đến 750nm. Tại vị trí của vân sáng bậc 3 của ánh sáng tím bước sóng 400nm còn có vân sáng của ánh sáng đơn sắc có bước sóng
Đáp án : D Phương pháp giải :
Sử dụng lí thuyết về giao thoa với ánh sáng trắng Hai vân sáng trùng nhau: x1 = x2 <=> k1λ1 = k2λ2 Lời giải chi tiết :
Vị trí của vân sáng bậc 3 của sáng tím trùng với vân sáng của ánh sáng đơn sắc khác Sử dụng điều kiện của 2 vân sáng trùng nhau ta có: \(\frac{{{k_1}{\lambda _1}D}}{a} = \frac{{{k_2}.{\lambda _2}D}}{a} \Leftrightarrow {k_1}{\lambda _1} = {k_2}.{\lambda _2} \Leftrightarrow 3.400 = {k_2}.{\lambda _2} \Leftrightarrow {\lambda _2} = \frac{{1200}}{{{k_2}}}\) trong đó \({k_1},{k_2}\) là số nguyên Mà: \(400 \le {\lambda _2} \le 750 \Leftrightarrow 400 < \frac{{1200}}{{{k_2}}} \le 750 \Rightarrow {k_2} = 2 \Rightarrow {\lambda _2} = 600nm\)
Câu 25 :
Trong một thí nghiệm Y-âng về giao thoa ánh sáng, bước sóng ánh sáng đơn sắc là 600nm, khoảng cách giữa hai khe hẹp là 1mm. Khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là 2m. Khoảng vân quan sát trên mà có giá trị bằng:
Đáp án : D Phương pháp giải :
Công thức tính khoảng vân: i = λD/a Lời giải chi tiết :
Ta có: \(i = \frac{{\lambda D}}{a} = {600.10^{ - 9}}.\frac{2}{{{{10}^{ - 3}}}} = 1,{2.10^{ - 3}}m = 1,2mm\)
Câu 26 :
Cường độ dòng điện tức thời trong mạch dao động LC có dạng $i= 0,02cos2000t(A)$. Tụ điện trong mạch có điện dung $5μF$. Độ tự cảm của cuộn cảm là:
Đáp án : A Phương pháp giải :
+ Đọc phương trình cường độ dòng điện trong mạch LC + Áp dụng biểu thức xác định tần số góc của mạch dao động LC: $\omega = \frac{1}{{\sqrt {LC} }}$ Lời giải chi tiết :
Từ phương trình cường độ dòng điện $i = 0,02cos2000t(A)$ Ta có: $ω = 2000 (rad/s)$ Mặt khác, ta có: $\omega = \dfrac{1}{{\sqrt {LC} }} \to L = \dfrac{1}{{{\omega ^2}C}} = \dfrac{1}{{{{2000}^2}{{.5.10}^{ - 6}}}} = 0,05H$
Câu 27 :
Cho phản ứng \(_1^2D + _1^2D \to _2^3He + n + 3,25MeV\). Phản ứng này là:
Đáp án : B Lời giải chi tiết :
\(_1^2D + _1^2D \to _2^3He + n + 3,25MeV\)là phản ứng nhiệt hạch
Câu 28 :
Giả sử các electron đến được anốt của tế bào quang điện đều bị hút về anốt, khi đó dòng quang điện có cường độ I = 0,32mA. Số electron thoát ra khỏi catốt trong mỗi giây là:
Đáp án : B Phương pháp giải :
Áp dụng biểu thức: \({I_{bh}} = {n_e}.e\) Lời giải chi tiết :
Ta có: Cường độ dòng quang điện khi đó là dòng quang điện bão hòa: \({I_{bh}} = {n_e}.\left| e \right| \to {n_e} = \frac{{{I_{bh}}}}{{\left| e \right|}} = \frac{{0,{{32.10}^{ - 3}}}}{{1,{{6.10}^{ - 19}}}} = {2.10^{15}}\) => Số electron thoát ra khỏi catốt trong mỗi giây là ne = 2.1015
Câu 29 :
Dùng chùm proton bắn phá hạt nhân \(_3^7Li\) đang đứng yên tạo ra 2 hạt nhân X giống nhau có cùng động năng là \(W\) nhưng bay theo hai hướng hợp với nhau một góc \(\varphi \) và không sinh ra tia gamma. Biết tổng năng lượng nghỉ của các hạt trước phản ứng chuyển nhiều hơn tổng năng lượng nghỉ của các hạt tạo thành là \(2W/3\). Coi khối lượng hạt nhân đo bằng đơn bị khối lượng nguyên tử gần bằng số khối của nó thì:
Đáp án : D Phương pháp giải :
+ Viết phương trình phản ứng + Dạng bài khi biết \(\widehat {\overrightarrow {{v_C}} ,\overrightarrow {{v_D}} } = \alpha \) (Xem lí thuyết) Lời giải chi tiết :
Phương trình: \(p + _3^7Li \to _2^4X + _2^4X\) Ta có: \({{\rm{W}}_{{d_p}}} + \Delta E = 2{{\rm{W}}_{{d_X}}} \to {{\rm{W}}_{{d_p}}} = 2{{\rm{W}}_{{d_X}}} - \Delta E = 2{\rm{W}} - \dfrac{2}{3}{\rm{W = }}\dfrac{4}{3}{\rm{W}}\) Mặt khác: \(\widehat {\overrightarrow {{v_X}} ,\overrightarrow {{v_X}} } = \varphi \) \(\begin{array}{l}P_p^2 = P_X^2 + P_X^2 + 2{P_X}{P_X}{\rm{cos}}\varphi \\ \leftrightarrow {m_p}{{\rm{W}}_{{d_p}}} = 2{m_X}{{\rm{W}}_{{d_X}}} + 2{m_X}{{\rm{W}}_{{d_X}}}{\rm{cos}}\varphi \\ \leftrightarrow \dfrac{4}{3}{\rm{W}} = 2.4{\rm{W}}(1 + c{\rm{os}}\varphi {\rm{)}} \to c{\rm{os}}\varphi = - \dfrac{5}{6}\end{array}\)
Câu 30 :
Cho mạch điện như hình vẽ, nguồn có suất điện động E=12V điện trở trong r = 1Ω, tụ có điện dung C=100μF, cuộn dây có hệ số tự cảm L=0,2H và điện trở là R0= 5Ω; điện trở R=18Ω. Ban đầu K đóng, khi trạng thái trong mạch đã ổn định người ta ngắt khoá K. Tính nhiệt lượng tỏa ra trên điện trở R trong thời gian từ khi ngắt K đến khi dao động trong mạch tắt hoàn toàn? 
Đáp án : C Phương pháp giải :
- Sử dụng định luật ohm: I = E /(R + r) - Năng lượng của mạch dao động: \(W = \dfrac{1}{2}L{i^2} + \dfrac{1}{2}C{u^2}\) Lời giải chi tiết :
Khi K đóng \(I_0= \dfrac{E}{(R +r+R_0)} =\dfrac{12}{( 18+1+5)}=0,5A\) Điện áp 2 đầu tụ C lúc đầu: \(U_0=I_0(R +R_0) = 0,5 .23=11,5V\) Năng lượng lúc đầu của mạch: \(\begin{array}{l}W = \dfrac{{CU_0^2}}{2} + \dfrac{{LI_0^2}}{2} = \dfrac{{{{10}^{ - 4}}.11,5_{}^2}}{2} + \dfrac{{0,2.0,5_{}^2}}{2}\\ = {0,66125.10^{ - 2}} + 0,025 = 0,0316125J\end{array}\) Năng lượng tỏa ra trên R và R0 tỉ lệ thuận với điện trở. \(\to \dfrac{R}{R_0}=\dfrac{18}{5}\) \(\to\) Nhiệt lượng tỏa ra chia thành 23 phần thì tỏa trên R 18 phần. Khi mạch tắt hoàn toàn thì năng lượng W chuyển thành nhiệt lượng tỏa ra trên R và R0 nên ta có: \(Q=W\) \(\to\) Nhiệt lượng tỏa ra trên R: \(Q_R = \dfrac{{18}}{{23}}W = \dfrac{{18}}{{23}}.0,0316125 = 0,024740217J \approx 0,02474J=24,74 mJ\).
Câu 31 :
Người ta dùng một Laze hoạt động dưới chế độ liên tục để khoan một tấm thép. Công suất của chùm laze là P = 10 W, đường kính của chùm sáng là 1 mm. Bề dày tấm thép là e = 2 mm và nhiệt độ ban đầu là 300C. Biết khối lượng riêng của thép D = 7800 kg/m3 ; Nhiệt dung riêng của thép c = 448 J/kg.độ ; nhiệt nóng chảy của thép L = 270 kJ/kg và điểm nóng chảy của thép tc = 15350C. Thời gian khoan thép là
Đáp án : A Phương pháp giải :
Sử dụng lí thuyết về laze (Xem lí thuyết phần 1) Lời giải chi tiết :
Ta có: + Thể tích thép nấu chảy: \(V = \frac{{\pi {d^2}}}{4}e = \frac{{\pi .{{({{10}^{ - 3}})}^2}}}{4}{2.10^{ - 3}} = 1,{57.10^{ - 9}}{m^3}\) + Khối lượng thép nấu cần chảy: \(m{\rm{ }} = {\rm{ }}DV{\rm{ }} = {\rm{ }}7800.1,{57.10^{ - 9}} = 1,{225.10^{ - 5}}\left( {kg} \right)\) + Nhiệt lượng cần thiết bằng tổng nhiệt lượng đưa thép đến nóng chảy và nhiệt làm chuyển thể: \(Q = mc\Delta t + mL = 1,{225.10^{ - 5}}.448\left( {1535 - 30} \right) + 1,{225.10^{ - 5}}{.270.10^3} = 11,569J\) Thời gian khoan thép: \(t = \frac{Q}{P} = \frac{{11,569}}{{10}} \approx 1,16s\)
Câu 32 :
Cho khối lượng của hạt nhân \({}_2^4He\); prôtôn và nơtron lần lượt là 4,0015 u; 1,0073 u và 1,0087 u.Lấy 1 u = 1,66.10–27 kg; c = 3.108 m/s; NA = 6,02.1023 mol–1. Năng lượng tỏa ra khi tạo thành 1 mol \({}_2^4He\) từ các nuclôn là
Đáp án : B Phương pháp giải :
+ Sử dụng định luật bảo toàn điện tích và số khối để viết phương trình phản ứng + Áp dụng công thức tính năng lượng toả ra hay thu vào của phản ứng hạt nhân ∆E = (mt – ms)c2 + Công thức tính số hạt chứa trong n (mol) chất: N = n.NA (NA = 6,02.1023 (số Avogadro)) Lời giải chi tiết :
Phương trình phản ứng: \(2{}_1^1p + 2{}_0^1n \to {}_2^4He\) 1MeV = 1,6.10-13J Năng lượng toả ra khi tạo thành một hạt nhân He là: \(\Delta E{\rm{ = (2}}{{\rm{m}}_p} + 2{m_n} - {m_{He}}){c^2} = 28,41075MeV\) Số hạt nhân nguyên tử He chứa trong 1 mol nguyên tử He là: N = 6,02.1023 \( \to \) Năng lượng tỏa ra khi tạo thành 1 mol heli là: \({\rm{E }} = {\rm{ }}N.\Delta E{\rm{ }} = {6,02.10^{23}}.28,41075{.1,6.10^{ - 13}} = {2,74.10^{12}}J\)
Câu 33 :
Khi điện tích trên tụ tăng từ $0$ lên $0,5{\rm{ }}\left( {\mu C} \right)$ thì đồng thời cường độ dòng điện trong mạch dao động LC lí tưởng giảm từ $3\pi \left( {mA} \right)$ xuống \(\dfrac{{3\sqrt 3 \pi }}{2}mA\) . Khoảng thời gian xảy ra sự biến thiên này là:
Đáp án : D Phương pháp giải :
+ Sử dụng vòng tròn lượng giác + Áp dụng công thức mối liên hệ giữa q0 và I0: \(\omega = \dfrac{{{I_0}}}{{{q_0}}}\) + Áp dụng công thức: \(\Delta \varphi = \omega \Delta t\) Lời giải chi tiết :
Ta có: - Khi $q = 0,i = 3\pi (mA) = {I_0}$ => khi \(i = \dfrac{{3\sqrt 3 \pi }}{2}mA = \dfrac{{{I_0}\sqrt 3 }}{2}\) Vẽ vòng tròn lượng giác, ta được: 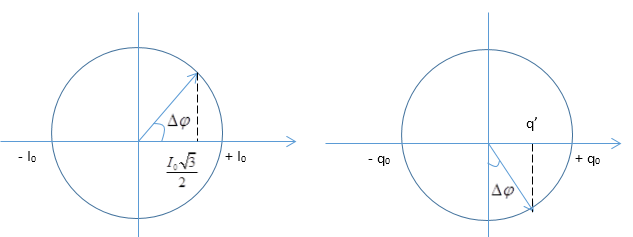 Từ vòng tròn lượng giác, ta có: ${\rm{cos}}\Delta \varphi {\rm{ = }}\dfrac{{\dfrac{{{I_0}\sqrt 3 }}{2}}}{{{I_0}}} = \dfrac{{\sqrt 3 }}{2} \to \Delta \varphi = \dfrac{\pi }{6}$ \(\begin{array}{l} \to q' = {q_0}\sin \Delta \varphi = {q_0}\sin \dfrac{\pi }{6} = \dfrac{{{q_0}}}{2} = 0,5\mu C \to {q_0} = 1\mu C\\ \to \omega = \dfrac{{{I_0}}}{{{q_0}}} = \dfrac{{3\pi {{.10}^{ - 3}}}}{{{{10}^{ - 6}}}} = 3\pi {.10^3}({\rm{r}}a{\rm{d}}/s)\end{array}\) Ta có: \(\Delta \varphi = \omega \Delta t \to \Delta t = \dfrac{{\Delta \varphi }}{\omega } = \dfrac{{\dfrac{\pi }{6}}}{{3\pi {{.10}^3}}} = \dfrac{1}{{18}}{.10^{ - 3}} = \dfrac{1}{{18}}ms\)
Câu 34 :
Một anten parabol, đặt tại một điểm A trên mặt đất, phát ra một sóng truyền theo phương làm với mặt phẳng ngang góc 450 hướng lên một vệ tinh địa tĩnh V. Coi trái đất là hình cầu, bán kính R=6380km. Vệ tinh địa tĩnh ở độ cao 35800km so với mặt đất. Sóng này truyền từ A đến V mất thời gian:
Đáp án : A Phương pháp giải :
+ Vẽ hình + Sử dụng hệ thức lượng trong tam giác + Vận dụng công thức : \(s = vt\) Lời giải chi tiết :
Ta có: 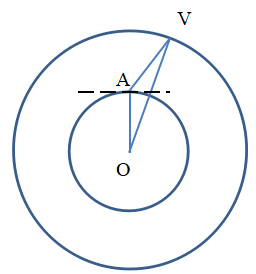 Áp dụng định lý hàm số cos, ta có: \(\begin{array}{l}O{V^2} = O{A^2} + A{V^2} - 2OA.AV.c{\rm{os13}}{{\rm{5}}^0}\\ \to AV = 37500km\end{array}\) Mặt khác, ta có: \(\begin{array}{l}AV = ct\\ \to t = \frac{{AV}}{c}=\frac{{37500.1000}}{{{{3.10}^8}}}=0,125{\rm{s}}\end{array}\)
Câu 35 :
Biết số Avôgađrô NA = 6,02.1023 hạt/mol và khối lượng của hạt nhân bằng số khối của nó. Số protôn có trong 0,27 gam \(_{13}^{^{27}}Al\) là
Đáp án : D Phương pháp giải :
Sử dụng lí thuyết về cấu tạo của hạt nhân nguyên tử và công thức tính liên hệ khối lượng và số hạt N = m.NA/A Lời giải chi tiết :
1 nguyên tử Al có 13 proton Số nguyên tử trong 0,27g Al là: N = m.NA/A = 0,27.6,02.1023/27 = 6,02.1021 Số proton trong 0,27g Al là: 13.N = 7,826.1022
Câu 36 :
Trong thí nghiệm Y-âng về giao thoa của ánh sáng đơn sắc, hai khe hẹp cách nhau \(1 mm\), mặt phẳng chứa hai khe cách màn quan sát \(1,5 m\). Khoảng cách giữa \(5\) vân sáng liên tiếp là \(3,6 mm\). Bước sóng của ánh sáng dùng trong thí nghiệm này bằng:
Đáp án : D Phương pháp giải :
+ Áp dụng công thức tính khoảng vân: \(i = \dfrac{{\lambda D}}{a}\) + Sử dụng lí thuyết khoảng cách giữa hai vân sáng liên tiếp bằng khoảng vân i. Lời giải chi tiết :
Khoảng cách giữa \(5\) vân sáng liên tiếp là \(3,6 mm = 4i\) => khoảng vân \(i = \dfrac{{3,6}}{4} = 0,9mm=0,9.10^{-3}m\) Ta có: \(a=1mm=10^{-3}m\) Bước sóng \(\lambda = \dfrac{{ia}}{D} = \dfrac{{0,9.10^{-3}.1.10^{-3}}}{{1,5}} =0,6.10^{-6}m= 0,6(\mu m)\)
Câu 37 :
Cho phản ứng phân hạch của Urani 235: \({}_{92}^{235}U + {}_0^1n \to {}_{42}^{95}Mo + {}_{57}^{139}La + 2{}_0^1n\). Biết khối lượng các hạt nhân: mU = 234,99u; mMo = 94,88u; mLa = 138,87u; mn = 1,0087u. Hỏi năng lượng tỏa ra khi 1 gam U phân hạch hết sẽ tương đương với năng lượng sinh ra khi đốt cháy bao nhiêu kg xăng? Biết rằng mỗi kg xăng cháy hết tỏa năng lượng 46.106 J.
Đáp án : D Phương pháp giải :
+ Công thức tính năng lượng toả ra của phản ứng: ∆E = (mt – ms)c2 (mt, ms lần lượt là tổng khối lượng của các hạt trước và sau phản ứng) + Công thức liên hệ giữa số hạt và khối lượng: N = (m/A)NA Lời giải chi tiết :
Năng lượng toả ra khi 1 hạt U phân hạch là: \(\Delta E = \left[ {\left( {{m_U} + {m_n}} \right) - \left( {{m_{Mo}} + {m_{La}} + 2{m_n}} \right)} \right]{c^2} = \left( {234,99 - 94,88 - 138,87 - 1,0087} \right)u{c^2} = 0,2313.931,5 = 215,5\,MeV\) 1 (g) U235 chứa: \(N = \frac{m}{A}{N_A} = \frac{1}{{235}}.6,{02.10^{23}} = 2,{56.10^{21}}\)hạt 1 gam U phân hạch hết toả năng lượng: \(E = N.\Delta E = 5,{52.10^{23}}MeV = 8,{832.10^{10}}J\) Lượng xăng cần sử dụng là: \(m = \frac{{8,{{832.10}^{10}}}}{{{{46.10}^6}}} = 1920kg\)
Câu 38 :
Hiện nay trong quặng thiên nhiên có chứa cả \(_{92}^{238}U\) và \(_{92}^{235}U\) theo tỉ lệ nguyên tử là 140 :1. Giả sử ở thời điểm tạo thành Trái Đất, tỷ lệ trên là 1:1. Hãy tính tuổi của Trái Đất. Biết chu kỳ bán rã của \(_{92}^{238}U\) là 4,5.109 năm, \(_{92}^{235}U\) có chu kỳ bán rã 7,13.108 năm.
Đáp án : A Phương pháp giải :
Sử dụng công thức: \(N = {N_0}{2^{ - \frac{t}{T}}}\) Lời giải chi tiết :
Gọi N0 là số nguyên tử của U238 và cũng là số nguyên tử của U235 ở thời điểm tạo thành trái đất. Số nguyên tử của chúng tại thời điểm t: \({N_1} = {N_0}{2^{ - \frac{t}{{{T_1}}}}};{N_2} = {N_0}{2^{ - \frac{t}{{{T_2}}}}}\) Theo đầu bài, ta có: \(\begin{array}{l}\frac{{{N_1}}}{{{N_2}}} = 140 = \frac{{{2^{ - \frac{t}{{{T_1}}}}}}}{{{2^{ - \frac{t}{{{T_2}}}}}}} = {2^{\frac{t}{{{T_2}}} - \frac{t}{{{T_1}}}}} = 140 \to \frac{t}{{{T_2}}} - \frac{t}{{{T_1}}} = \log _2^{140} = 7,13\\ \to t\left( {\frac{1}{{{T_2}}} - \frac{1}{{{T_1}}}} \right) = 7,13 \to t = 60,{4.10^8}\end{array}\)
Câu 39 :
Một nguyên tử chuyển từ trạng thái dừng Em sang trạng thái dừng En (Em < En) khi hấp thụ một photon có năng lượng hf. Chọn câu đúng:
Đáp án : A Lời giải chi tiết :
Ta có: Khi nguyên tử chuyển từ trạng thái dừng có năng lượng En sang trạng thái có năng lượng Em < En thì nó phát ra một photon có năng lượng $\varepsilon = {E_n} - {E_m}$.
Câu 40 :
Một tụ điện có điện dung C được nạp điện tới điện tích q. Khi nối tụ với cuộn cảm thuần có độ tự cảm L1 thì trong mạch có dao động điện từ riêng với cường độ dòng điện cực đại bằng 70mA. Khi nối tụ với cuộn cảm thuần có độ tự cảm L2 thì trong mạch có dao động điện từ riêng với cường độ dòng điện cực dại bằng 35mA. Nếu nối tụ với cuộn cảm thuần có độ tự cảm ${L_3} = 13{L_1} + 9{L_2}$ thì trong mạch có cường độ dòng điện cực đại bằng
Đáp án : A Phương pháp giải :
+ Áp dụng biểu thức tính cường độ dòng điện cực đại: I0 = ωq0 + Áp dụng biểu thức xác định tần số góc của mạch dao động LC: $\omega = \frac{1}{{\sqrt {LC} }}$ Lời giải chi tiết :
Cách 1 : Ta có: \(\begin{array}{l}{I_1} = {\omega _1}q = \frac{q}{{\sqrt {{L_1}C} }} = > {L_1} = \frac{{{q^2}}}{{{I_1}^2C}}\\{I_2} = {\omega _2}q = \frac{q}{{\sqrt {{L_2}C} }} = > {L_2} = \frac{{{q^2}}}{{{I_2}^2C}}\end{array}\) => Khi sử dụng cuộn cảm có độ tự cảm \({L_3} = 13{L_1} + 9{L_2}\) thì cường độ dòng điện cực đại là : \({I_3} = \frac{q}{{\sqrt {{L_3}C} }} = \frac{q}{{\sqrt {(13\frac{{{q^2}}}{{{I_1}^2C}} + 9\frac{{{q^2}}}{{{I_2}^2C}})C} }} = \frac{{{I_1}{I_2}}}{{\sqrt {13{I_2}^2 + 9{I_1}^2} }} = 10mA\) Cách 2: Ta có: \(\begin{array}{l}{I_1} = {\omega _1}q = \frac{q}{{\sqrt {{L_1}C} }};{I_2} = {\omega _2}q = \frac{q}{{\sqrt {{L_2}C} }}\\ \to \frac{{{I_1}}}{{{I_2}}} = \sqrt {\frac{{{L_2}}}{{{L_1}}}} = \frac{{70}}{{35}} \to \frac{{{L_2}}}{{{L_1}}} = 4\\ \to {L_2} = 4{L_1}\end{array}\) \(\begin{array}{l}{I_3} = \frac{q}{{\sqrt {{L_3}C} }} \to \frac{{{I_3}}}{{{I_1}}} = \sqrt {\frac{{{L_1}}}{{{L_3}}}} = \sqrt {\frac{{{L_1}}}{{13{L_1} + 9{L_2}}}} = \sqrt {\frac{{{L_1}}}{{13{L_1} + 9.4{L_1}}}} = \frac{1}{7}\\ \to {I_3} = \frac{{{I_1}}}{7} = \frac{{70}}{7} = 10mA\end{array}\) |




















Danh sách bình luận