Trắc nghiệm Bài 4: Định lí Toán 7 Cánh diềuĐề bài
Câu 1 :
Trong các câu sau, câu nào cho một định lí
Câu 2 :
Cho định lý: “Nếu hai đường thẳng song song cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau” (xem hình vẽ dưới đây). Giả thiết của định lý là 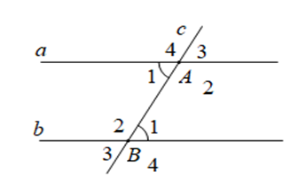
Câu 3 :
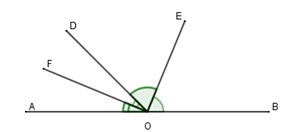
Cho định lý: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông” (hình vẽ). Giả thiết, kết luận của định lý là: 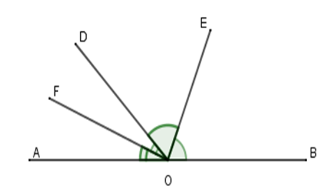
Câu 4 :
Phát biểu định lý sau bằng lời: 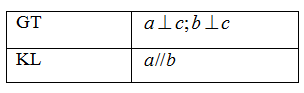
Câu 5 :
Định lý sau được phát biểu thành lời là: 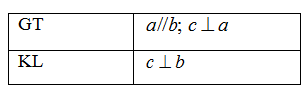
Câu 6 :
Chọn câu đúng.
Câu 7 :
Chứng minh định lý là
Câu 8 :
Trong các câu sau, câu nào không cho một định lí:
Câu 9 :
Cho định lý: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông” (hình vẽ). Giả thiết, kết luận của định lý là:
Câu 10 :
Phần giả thiết: \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\), \(\widehat {{A_1}} = \widehat {{B_1}}\) (tham khảo hình vẽ) là của định lý nào dưới đây?
Câu 11 :
Chọn câu đúng.
Câu 12 :
Chọn khẳng định đúng:
Câu 13 :
Chọn câu sai:
Lời giải và đáp án
Câu 1 :
Trong các câu sau, câu nào cho một định lí
Đáp án : A Phương pháp giải :
Sử dụng lý thuyết về định lý: Một tính chất được khẳng định là đúng bằng suy luận gọi là một định lí. Lời giải chi tiết :
Định lý: “Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.” Chú ý
Câu D sai vì ta cần hai đường thẳng phân biệt.
Câu 2 :
Cho định lý: “Nếu hai đường thẳng song song cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau” (xem hình vẽ dưới đây). Giả thiết của định lý là 
Đáp án : B Phương pháp giải :
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra Lời giải chi tiết :
Giả thiết của định lý trên là \(a//b,\) \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\)
Câu 3 :
Cho định lý: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông” (hình vẽ). Giả thiết, kết luận của định lý là: 
Đáp án : A Phương pháp giải :
Một tính chất được khẳng định là đúng bằng suy luận gọi là một định lí. Lời giải chi tiết :
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\). Kết luận: \(OE \bot OF\)
Câu 4 :
Phát biểu định lý sau bằng lời: 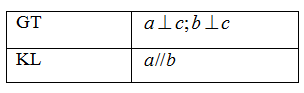
Đáp án : C Phương pháp giải :
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra Lời giải chi tiết :
Định lý: Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.
Câu 5 :
Định lý sau được phát biểu thành lời là: 
Đáp án : A Phương pháp giải :
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra. Lời giải chi tiết :
Định lý: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
Câu 6 :
Chọn câu đúng.
Đáp án : D Phương pháp giải :
Sử dụng lý thuyết về định lý. Lời giải chi tiết :
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra
Câu 7 :
Chứng minh định lý là
Đáp án : A Phương pháp giải :
Sử dụng định nghĩa “chứng minh định lý”. Lời giải chi tiết :
Chứng minh định lý là dùng lập luận để từ giả thiết và các khẳng định đúng đã biết suy ra kết luận.
Câu 8 :
Trong các câu sau, câu nào không cho một định lí:
Đáp án : D Phương pháp giải :
Sử dụng nhận xét về định lý: Một tính chất được khẳng định là đúng bằng suy luận gọi là một định lí. Lời giải chi tiết :
+ “Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.” + “Nếu một đường thẳng cắt 2 đường thẳng song song thì tạo ra các cặp góc so le trong, cặp góc đồng vị bằng nhau.” + “Hai góc đối đỉnh thì bằng nhau” Câu D không là định lí vì khẳng định D sai
Câu 9 :
Cho định lý: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông” (hình vẽ). Giả thiết, kết luận của định lý là:
Đáp án : A Phương pháp giải :
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra Lời giải chi tiết :
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\). Kết luận: \(OE \bot OF\)
Câu 10 :
Phần giả thiết: \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\), \(\widehat {{A_1}} = \widehat {{B_1}}\) (tham khảo hình vẽ) là của định lý nào dưới đây?
Đáp án : B Phương pháp giải :
Xét vị trí của góc A1 so với góc B1 rồi xét giả thiết của từng định lý Lời giải chi tiết :
Đường thẳng c cắt đường thẳng a và b, tạo thành cặp góc so le trong bằng nhau (\(\widehat {{A_1}} = \widehat {{B_1}}\)) thì a // b Vậy định lý là: “Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc so le trong bằng nhau thì hai đường thẳng đó song song”
Câu 11 :
Chọn câu đúng.
Đáp án : D Phương pháp giải :
Lý thuyết về định lí Lời giải chi tiết :
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra
Câu 12 :
Chọn khẳng định đúng:
Đáp án : D Phương pháp giải :
Xét tính đúng, sai của từng khẳng định Lời giải chi tiết :
+ Tia phân giác của 2 góc đối đỉnh là đối nhau nên A sai + 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau nên B sai + 2 góc đối đỉnh thì bằng nhau nhưng hai góc bằng nhau chưa chắc đã đối đỉnh nên C sai + 2 tia phân giác của 2 góc đối đỉnh là 2 tia đối nhau nên là 2 cạnh của 1 góc bẹt. Do đó D đúng.
Câu 13 :
Chọn câu sai:
Đáp án : A Phương pháp giải :
Lý thuyết về định lí Lời giải chi tiết :
Khẳng định A sai vì định lí thường được phát biểu ở dạng: “ Nếu … thì …” Các khẳng định B,C,D đúng .
|














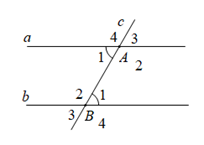





Danh sách bình luận