Trắc nghiệm Bài 3: Phép tính lũy thừa với số mũ tự nhiên của một số hữu tỉ Toán 7 Cánh diềuĐề bài
Câu 1 :
Tính: \({\left( {\frac{{ - 3}}{7}} \right)^3}\)
Câu 2 :
Tính 94 . 35
Câu 3 :
Tính: \(8:{\left( {\frac{2}{3} - \frac{3}{4}} \right)^2}\)
Câu 4 :
Chọn khẳng định đúng:
Câu 5 :
Tìm x, biết: 27x . 34 = 95
Câu 6 :
Tính A = 1 + 3 + 32 +…+ 32022
Câu 7 :
Biết khối lượng của Mặt Trời là khoảng 1 988 550 . 1021 tấn, khối lượng của Trái Đất khoảng 0,6 . 1022 tấn. Khối lượng của Mặt Trời gấp khoảng bao nhiêu lần khối lượng Trái Đất?
Câu 8 :
Tìm x biết: (2x+1)3 – 1 = -344
Câu 9 :
Tính giá trị biểu thức \(M = \frac{{ - {x^2} + 2x - 1}}{{{{(2x)}^3}}}\) tại x = 3
Câu 10 :
Chọn câu sai. Với hai số hữu tỉ \(a,\,b\) và các số tự nhiên \(m,\,n\) ta có
Câu 11 :
Tính \({\left( {\dfrac{2}{3}} \right)^3}\)
Câu 12 :
Chọn khẳng định đúng. Với số hữu tỉ \(x\) ta có
Câu 13 :
Kết quả của phép tính \({\left( {\dfrac{1}{7}} \right)^2}{.7^2}\) là:
Câu 14 :
Chọn câu sai.
Câu 15 :
Số ${x^{12}}$ (với $x \ne 0$) không bằng số nào trong các số sau đây ?
Câu 16 :
Số ${2^{24}}$ viết dưới dạng lũy thừa có số mũ $8$ là:
Câu 17 :
Số $x$ sao cho ${2^x}\; = {\left( {{2^2}} \right)^5}$ là :
Câu 18 :
Số $a$ thỏa mãn $a:{\left( {\dfrac{1}{3}} \right)^4} = {\left( {\dfrac{1}{3}} \right)^3}$ là :
Câu 19 :
Giá trị nhỏ nhất của biểu thức ${\left( {x + \dfrac{1}{3}} \right)^2} + \dfrac{1}{{100}}$ đạt được là:
Câu 20 :
Cho ${20^n}\;:\;{5^n} = 4$ thì :
Câu 21 :
Cho biểu thức $A = \dfrac{{{2^7}{{.9}^3}}}{{{6^5}{{.8}^2}}}$. Chọn khẳng định đúng.
Câu 22 :
Giá trị của biểu thức \(\dfrac{{{4^6}{{.9}^5} + {6^9}.120}}{{{8^4}{{.3}^{12}} - {6^{11}}}}\) là
Câu 23 :
Tìm \(x\), biết \({\left( {5x - 1} \right)^6} = 729\)
Câu 24 :
Có bao nhiêu giá trị của \(x\) thỏa mãn \({\left( {2x + 1} \right)^3} = - 0,001\)?
Câu 25 :
Tìm số tự nhiên \(n\) thỏa mãn \({5^n} + {5^{n + 2}} = 650\).
Câu 26 :
Cho biết : \({1^2} + {2^2} + {3^2} + ... + {10^2} = 385\) . Tính nhanh giá trị của biểu thức sau: \(S = \left( {{{12}^2} + {{14}^2} + {{16}^2} + {{18}^2} + {{20}^2}} \right) - \left( {{1^2} + {3^2} + {5^2} + {7^2} + {9^2}} \right)\)
Câu 27 :
Cho \(A = 1 - \dfrac{3}{4} + {\left( {\dfrac{3}{4}} \right)^2} - {\left( {\dfrac{3}{4}} \right)^3} + {\left( {\dfrac{3}{4}} \right)^4} - ... - {\left( {\dfrac{3}{4}} \right)^{2017}} + {\left( {\dfrac{3}{4}} \right)^{2018}}\). Chọn đáp án đúng.
Lời giải và đáp án
Câu 1 :
Tính: \({\left( {\frac{{ - 3}}{7}} \right)^3}\)
Đáp án : C Phương pháp giải :
Sử dụng định nghĩa lũy thừa của một số hữu tỉ:
Lời giải chi tiết :
\({\left( {\frac{{ - 3}}{7}} \right)^3} = \left( {\frac{{ - 3}}{7}} \right).\left( {\frac{{ - 3}}{7}} \right).\left( {\frac{{ - 3}}{7}} \right) = \frac{{( - 3).( - 3).( - 3)}}{{7.7.7}} = \frac{{ - 27}}{{343}}\)
Câu 2 :
Tính 94 . 35
Đáp án : D Phương pháp giải :
Bước 1: Đưa 2 lũy thừa về dạng 2 lũy thừa có cùng cơ số Bước 2: Sử dụng công thức nhân 2 lũy thừa cùng cơ số: am . an = am+n Chú ý: (ap)q = ap.q Lời giải chi tiết :
Ta có: 94 . 35 = (32)4 . 35 = 32.4 . 35 = 38 . 35 = 38+5 = 313
Câu 3 :
Tính: \(8:{\left( {\frac{2}{3} - \frac{3}{4}} \right)^2}\)
Đáp án : C Phương pháp giải :
Bước 1: Tính lũy thừa Bước 2: Chia 2 số hữu tỉ Lời giải chi tiết :
\(8:{\left( {\frac{2}{3} - \frac{3}{4}} \right)^2} = 8:{\left( {\frac{8}{{12}} - \frac{9}{{12}}} \right)^2} = 8:{\left( {\frac{{ - 1}}{{12}}} \right)^2} = 8:\frac{1}{{144}} = 8.144 = 1152\)
Câu 4 :
Chọn khẳng định đúng:
Đáp án : D Phương pháp giải :
Sử dụng các công thức: xm : xn = xm-n (\(x \ne 0;m \ge n\)) xm . xn = xm+n (xm)n = xm.n (-x)m = xm ( với m chẵn) (-x)m = - xm ( với m lẻ) Lời giải chi tiết :
+) (-4)3 . 45 = - 43 . 45 = - 43+5 = - 48 Vậy A sai +) am : an = am-n \((a \ne 0; m \ge n)\) Vậy B sai +) (-6)2021 = - 62021 ( vì 2021 là số lẻ) Vậy C sai +) [(-3)2]5 = (32)5 = 32.5 = 310 Vậy D đúng
Câu 5 :
Tìm x, biết: 27x . 34 = 95
Đáp án : A Phương pháp giải :
Đưa các lũy thừa về dạng các lũy thừa có cùng cơ số Với a \( \ne \)0; a \( \ne \) 1 thì am = an khi m = n Lời giải chi tiết :
27x . 34 = 95 (33)x . 34 = (32)5 33.x . 34 = 310 33x = 310 : 34 33x = 310-4 33x = 36 3x = 6 x = 6 : 3 x = 2 Vậy x = 2
Câu 6 :
Tính A = 1 + 3 + 32 +…+ 32022
Đáp án : D Phương pháp giải :
Phát hiện quy luật của tổng Bước 1: Tìm 3.A Bước 2: Thực hiện tính 3A – A Bước 3: Tính A Lời giải chi tiết :
Ta có: A = 1 + 3 + 32 +…+ 32022 suy ra 3.A = 3. ( 1 + 3 + 32 +…+ 32022) = 3 + 32 + 33 +…+ 32023 do đó 3. A – A = 3 + 32 + 33 +…+ 32023 – (1 + 3 + 32 +…+ 32022) 2A = 3 + 32 + 33 +…+ 32023 – 1 - 3 - 32 - …- 32022 = 32023 – 1 suy ra \( A = \frac{{{3^{2023}} - 1}}{2}\)
Câu 7 :
Biết khối lượng của Mặt Trời là khoảng 1 988 550 . 1021 tấn, khối lượng của Trái Đất khoảng 0,6 . 1022 tấn. Khối lượng của Mặt Trời gấp khoảng bao nhiêu lần khối lượng Trái Đất?
Đáp án : B Phương pháp giải :
Tính tỉ số khối lượng Mặt Trời : khối lượng Trái Đất Lời giải chi tiết :
Khối lượng của Mặt Trời gấp khoảng số lần khối lượng Trái Đất là: \(\frac{{1{\rm{ }}988{\rm{ }}550{\rm{ }}.{\rm{ }}{{10}^{21}}}}{{0,{{6.10}^{22}}}} = \frac{{1{\rm{ }}988{\rm{ }}550{\rm{ }}.{\rm{ }}{{10}^{21}}}}{{{{6.10}^{21}}}} = \frac{1{\rm{ }}988{\rm{ }}550}{6} = 331425\) ( lần)
Câu 8 :
Tìm x biết: (2x+1)3 – 1 = -344
Đáp án : D Phương pháp giải :
Đưa về dạng A3 = B3, rồi suy ra A = B Lời giải chi tiết :
(2x+1)3 – 1 = -344 (2x+1)3 = -344 + 1 (2x+1)3 = -343 (2x+1)3 = (-7)3 2x + 1 = -7 2x = -7 – 1 2x = -8 x = -4 Vậy x = -4
Câu 9 :
Tính giá trị biểu thức \(M = \frac{{ - {x^2} + 2x - 1}}{{{{(2x)}^3}}}\) tại x = 3
Đáp án : B Phương pháp giải :
Thay giá trị x = 3 vào biểu thức rồi tính Lời giải chi tiết :
Thay x = 3 vào M ta được: \(\begin{array}{l}M = \frac{{ - {x^2} + 2x - 1}}{{{{(2x)}^3}}}\\ = \frac{{ - {3^2} + 2.3 - 1}}{{{{(2.3)}^3}}}\\ = \frac{{ - 9 + 6 - 1}}{{{6^3}}}\\ = \frac{{ - 4}}{{216}}\\ = \frac{{ - 1}}{{54}}\end{array}\)
Câu 10 :
Chọn câu sai. Với hai số hữu tỉ \(a,\,b\) và các số tự nhiên \(m,\,n\) ta có
Đáp án : C Lời giải chi tiết :
Ta có ${a^m}.{a^n} = {a^{m + n}}$, ${\left( {a.b} \right)^m} = {a^m}.{b^m}$ và \({\left( {{a^m}} \right)^n} = {a^{m.n}}\) nên C sai.
Câu 11 :
Tính \({\left( {\dfrac{2}{3}} \right)^3}\)
Đáp án : B Phương pháp giải :
Sử dụng công thức \({\left( {\dfrac{a}{b}} \right)^n} = \dfrac{{{a^n}}}{{{b^n}}}\) Lời giải chi tiết :
Ta có \({\left( {\dfrac{2}{3}} \right)^3}\)\( = \dfrac{{{2^3}}}{{{3^3}}} = \dfrac{8}{{27}}\)
Câu 12 :
Chọn khẳng định đúng. Với số hữu tỉ \(x\) ta có
Đáp án : D Lời giải chi tiết :
Ta có \({x^1} = x;\)\({x^0} = 1\)\(\left( {x \ne 0} \right)\) nên A, B, C sai ${\left( {\dfrac{x}{y}} \right)^n} = \dfrac{{{x^n}}}{y^n}\left( {y \ne 0;\,n \in \mathbb{N}} \right)$ nên D đúng. Chú ý
Một số em chọn nhầm đáp án C do thiếu điều kiện $x \ne 0$.
Câu 13 :
Kết quả của phép tính \({\left( {\dfrac{1}{7}} \right)^2}{.7^2}\) là:
Đáp án : D Phương pháp giải :
Sử dụng công thức ${\left( {\dfrac{x}{y}} \right)^n} = \dfrac{{{x^n}}}{y^n}\left( {y \ne 0;\,n \in \mathbb{N}} \right)$ rồi thực hiện phép nhân. Lời giải chi tiết :
Ta có \({\left( {\dfrac{1}{7}} \right)^2}{.7^2} = \dfrac{1}{{{7^2}}}{.7^2} = \dfrac{{{7^2}}}{{{7^2}}} = 1\)
Câu 14 :
Chọn câu sai.
Đáp án : B Phương pháp giải :
Sử dụng công thức lũy thừa để tính toán: \({x^1} = x;\)\({x^0} = 1\)\(\left( {x \ne 0} \right)\) \({x^m}.{x^n} = {x^{m + n}}\); \({x^m}:{x^n} = {x^{m - n}}\)\(\left( {x \ne 0,m \ge n} \right)\) Lời giải chi tiết :
Ta có ${\left( {-2019} \right)^0} = 1$ nên A đúng. +) ${4^6}:{\rm{ }}{4^4} = {4^2} = 16$ nên C đúng +) ${\left( {-3} \right)^3}.{\left( {-{\rm{ }}3} \right)^{{\rm{ }}2}} = {\left( { - 3} \right)^{3 + 2}} = {\left( { - 3} \right)^5}$nên D đúng +) $\left( {0,5} \right).{\left( {0,5} \right)^2} = {\left( {0,5} \right)^3} = {\left( {\dfrac{1}{2}} \right)^3} = \dfrac{1}{8}$ nên B sai.
Câu 15 :
Số ${x^{12}}$ (với $x \ne 0$) không bằng số nào trong các số sau đây ?
Đáp án : C Phương pháp giải :
Ta áp dụng các công thức sau: ${x^m}.{x^n} = {x^{m + n}};{x^m}:{x^n} = {x^{m - n}}$$\left( {m \ge n,x \ne 0;m,n \in {N^ * }} \right)$, ${\left( {{x^m}} \right)^n} = {x^{m.n}}$ Lời giải chi tiết :
Ta có +) ${x^{18}}:{x^6} = {x^{18 - 6}} = {x^{12}}(x\; \ne 0)$ nên A đúng. +) ${x^4}.{\rm{ }}{x^8} = {x^{4 + 8}} = {x^{12}}$ nên B đúng. + ${\left( {{x^3}} \right)^4} = {x^{3.4}} = {x^{12}}$ nên D đúng. Ta thấy ở đáp án C: \({x^2}.{x^6} = {x^{2 + 6}} = {x^8} \ne {x^{12}}\) nên C sai.
Câu 16 :
Số ${2^{24}}$ viết dưới dạng lũy thừa có số mũ $8$ là:
Đáp án : A Phương pháp giải :
Áp dụng công thức ${\left( {{x^m}} \right)^n} = {x^{m.n}}$để tính toán Lời giải chi tiết :
Ta có: \({2^{24}} = {2^{3.8}} = {\left( {{2^3}} \right)^8} = {8^8}\)
Câu 17 :
Số $x$ sao cho ${2^x}\; = {\left( {{2^2}} \right)^5}$ là :
Đáp án : D Phương pháp giải :
Áp dụng công thức lũy thừa của lũy thừa \({({x^m})^n} = {x^{m.n}}\) đưa hai lũy thừa về cùng cơ số và so sánh số mũ. Lời giải chi tiết :
${2^x}\; = {\left( {{2^2}} \right)^5} \Leftrightarrow {2^x} = {2^{2.5}} \Leftrightarrow {2^x} = {2^{10}} \Leftrightarrow x = 10$
Câu 18 :
Số $a$ thỏa mãn $a:{\left( {\dfrac{1}{3}} \right)^4} = {\left( {\dfrac{1}{3}} \right)^3}$ là :
Đáp án : B Phương pháp giải :
Áp dụng công thức nhân hai lũy thừa cùng cơ số ${x^m}.{x^n} = {x^{m + n}}$ Lời giải chi tiết :
$a{\rm{ }}:{\left( {\dfrac{1}{3}} \right)^4} = {\left( {\dfrac{1}{3}} \right)^3}$ $a = {\left( {\dfrac{1}{3}} \right)^3}.{\left( {\dfrac{1}{3}} \right)^4}$ $a = {\left( {\dfrac{1}{3}} \right)^{3 + 4}}$ $a = {\left( {\dfrac{1}{3}} \right)^7}$
Câu 19 :
Giá trị nhỏ nhất của biểu thức ${\left( {x + \dfrac{1}{3}} \right)^2} + \dfrac{1}{{100}}$ đạt được là:
Đáp án : C Phương pháp giải :
Dùng phương pháp đánh giá biểu thức, sử dụng \({x^2} \ge 0,\forall x\). Lời giải chi tiết :
Ta có: ${\left( {x + \dfrac{1}{3}} \right)^2} \ge 0 $ với mọi $x$ $\Rightarrow {\left( {x + \dfrac{1}{3}} \right)^2} + \dfrac{1}{{100}} \ge 0+ \dfrac{1}{{100}}$ $\Rightarrow {\left( {x + \dfrac{1}{3}} \right)^2} + \dfrac{1}{{100}} \ge \dfrac{1}{{100}}$ Do đó GTNN biểu thức đạt được là \(\dfrac{1}{{100}}\) khi và chỉ khi \((x + \dfrac{1}{3})^2 = 0\) \(\Rightarrow x + \dfrac{1}{3} = 0\) hay \(x = - \dfrac{1}{3}\). Vậy giá trị nhỏ nhất cần tìm là $\dfrac{1}{100}.$
Câu 20 :
Cho ${20^n}\;:\;{5^n} = 4$ thì :
Đáp án : D Phương pháp giải :
Áp dụng công thức ${x^m}:{y^m} = {\left( {x:y} \right)^m}$$\left( {y \ne 0;m \in {N^ * }} \right)$ Lời giải chi tiết :
\({20^n}\;:\;{5^n} = 4\) \({(20:5)^n} = 4\) \({4^n} = 4\) \(n = 1\)
Câu 21 :
Cho biểu thức $A = \dfrac{{{2^7}{{.9}^3}}}{{{6^5}{{.8}^2}}}$. Chọn khẳng định đúng.
Đáp án : B Phương pháp giải :
Ta áp dụng công thức sau để tính toán * ${x^m}.{x^n} = \underbrace {x.x.x....x}_m.\underbrace {x...x}_n = {x^{m + n}}$ *${x^m}:{x^n} = \dfrac{{{x^m}}}{{{x^n}}} = {x^{m - n}}$ ($m \ge n$) * \({x^{m.n}} = {\left( {{x^m}} \right)^n}\) Lời giải chi tiết :
$A = \dfrac{{{2^7}{{.9}^3}}}{{{6^5}{{.8}^2}}} = \dfrac{{{2^7}.{{\left( {{3^2}} \right)}^3}}}{{{2^5}{{.3}^5}.{{\left( {{2^3}} \right)}^2}}} = \dfrac{{{2^7}{{.3}^6}}}{{{2^5}{{.2}^6}{{.3}^5}}} = \dfrac{{{2^7}{{.3}^6}}}{{{2^{11}}{{.3}^5}}} = \dfrac{{1.3}}{{{2^4}.1}} = \dfrac{3}{{16}}$
Câu 22 :
Giá trị của biểu thức \(\dfrac{{{4^6}{{.9}^5} + {6^9}.120}}{{{8^4}{{.3}^{12}} - {6^{11}}}}\) là
Đáp án : A Phương pháp giải :
Sử dụng công thức \({x^{m.n}} = {\left( {{x^m}} \right)^n}\) và \({\left( {x.y} \right)^m} = {x^m}.{y^m}\) để biển đổi và tính toán. Lời giải chi tiết :
Ta có \(\dfrac{{{4^6}{{.9}^5} + {6^9}.120}}{{{8^4}{{.3}^{12}} - {6^{11}}}} = \dfrac{{{{\left( {{2^2}} \right)}^6}.{{\left( {{3^2}} \right)}^5} + {6^9}.120}}{{{{\left( {{2^3}} \right)}^4}{{.3}^{12}} - {6^{11}}}}\)\( = \dfrac{{{2^{12}}{{.3}^{10}} + {6^9}.6.20}}{{{2^{12}}{{.3}^{12}} - {6^{11}}}} = \dfrac{{{2^2}{{.2}^{10}}{{.3}^{10}} + {6^{10}}.20}}{{{{\left( {2.3} \right)}^{12}} - {6^{11}}}}\)\( = \dfrac{{{2^2}{{.6}^{10}} + {6^{10}}.20}}{{{6^{12}} - {6^{11}}}}\)\( = \dfrac{{{6^{10}}\left( {{2^2} + 20} \right)}}{{{6^{10}}\left( {{6^2} - 6} \right)}} = \dfrac{{24}}{{30}} = \dfrac{4}{5}\)
Câu 23 :
Tìm \(x\), biết \({\left( {5x - 1} \right)^6} = 729\)
Đáp án : C Phương pháp giải :
Áp dụng các công thức sau để tìm $x$ *${x^{2n}} = {a^{2n}} \Rightarrow x = a$ hoặc $x = - a$ *${x^{2n + 1}} = {a^{2n + 1}} \Rightarrow x = a$ Lời giải chi tiết :
\({\left( {5x - 1} \right)^6} = 729\) \({\left( {5x - 1} \right)^6} = {(3)^6}\) Trường hợp 1: $\begin{array}{l}5x-1 = 3\\5x = 4\\x = \dfrac{4}{5}\end{array}$ Trường hợp 2: $\begin{array}{l}5x-1 = - 3\\5x = - 2\\x = - \dfrac{2}{5}\end{array}$ Vậy \(x = \dfrac{4}{5}\); \(x = - \dfrac{2}{5}\)
Câu 24 :
Có bao nhiêu giá trị của \(x\) thỏa mãn \({\left( {2x + 1} \right)^3} = - 0,001\)?
Đáp án : B Phương pháp giải :
Nếu \(n \in N\) lẻ mà \({a^n} = {b^n}\) thì \(a = b\) Lời giải chi tiết :
\({\left( {2x + 1} \right)^3} = - {0,1^3} = {\left( { - 0,1} \right)^3}\) \(2x + 1 = - 0,1\) \(2x = - 0,1 - 1\) \(2x = - 1,1\) \(x = - 1,1:2\) \(x = - 0,55\) Vậy $x = - 0,55$. Vậy có 1 giá trị của x.
Câu 25 :
Tìm số tự nhiên \(n\) thỏa mãn \({5^n} + {5^{n + 2}} = 650\).
Đáp án : B Phương pháp giải :
Áp dụng công thức sau để tìm $n$ $a \ne 0;a \ne \pm 1$ , nếu ${a^m} = {a^n}$ thì $m = n$ Lời giải chi tiết :
\({5^n} + {5^{n + 2}} = 650\) \({5^n} + {5^n}{.5^2} = 650\) \({5^n}\left( {1 + {5^2}} \right) = 650\) \({5^n}\left( {1 + 25} \right) = 650\) \({5^n}.26 = 650\) \({5^n} = 650:26\) \({5^n} = 25\) \({5^n} = {5^2}\) \(n = 2\) Vậy $n = 2$
Câu 26 :
Cho biết : \({1^2} + {2^2} + {3^2} + ... + {10^2} = 385\) . Tính nhanh giá trị của biểu thức sau: \(S = \left( {{{12}^2} + {{14}^2} + {{16}^2} + {{18}^2} + {{20}^2}} \right) - \left( {{1^2} + {3^2} + {5^2} + {7^2} + {9^2}} \right)\)
Đáp án : A Phương pháp giải :
Ta biến đổi biểu thức cần tính sao cho xuất hiện giả thiết đề bài cho. Từ đó thay vào ta sẽ tính được giá trị của biểu thức Lời giải chi tiết :
Ta có: \({1^2} + {2^2} + {3^2} + ... + {10^2} = 385\) Suy ra \({1^2} + {3^2} + {5^2} + {7^2} + {9^2} = 385 - \left( {{2^2} + {4^2} + {6^2} + {8^2} + {{10}^2}} \right) = 385 - {2^2}\left( {{1^2} + {2^2} + {3^2} + {4^2} + {5^2}} \right)\) Và \({12^2} + {14^2} + {16^2} + {18^2} + {20^2} = {2^2}.\left( {{6^2} + {7^2} + {8^2} + {9^2} + {{10}^2}} \right)\) Suy ra \(\) \(S = {2^2}.\left( {{6^2} + {7^2} + {8^2} + {9^2} + {{10}^2}} \right) - 385 + {2^2}\left( {{1^2} + {2^2} + {3^2} + {4^2} + {5^2}} \right)\) \(S = {2^2}\left( {{1^2} + {2^2} + {3^2} + {4^2} + {5^2} + {6^2} + {7^2} + {8^2} + {9^2} + {{10}^2}} \right) - 385 = 4.385 - 385 = 1155\) Vậy $S{\rm{ }} = {\rm{ }}1155$.
Câu 27 :
Cho \(A = 1 - \dfrac{3}{4} + {\left( {\dfrac{3}{4}} \right)^2} - {\left( {\dfrac{3}{4}} \right)^3} + {\left( {\dfrac{3}{4}} \right)^4} - ... - {\left( {\dfrac{3}{4}} \right)^{2017}} + {\left( {\dfrac{3}{4}} \right)^{2018}}\). Chọn đáp án đúng.
Đáp án : A Phương pháp giải :
+ Nhân \(A\) với \(\dfrac{3}{4}\) rồi thực hiện cộng \(A\) với \(\dfrac{3}{4}A\), sau đó thu gọn kết quả và suy ra \(A\). + Sử dụng: Khi \(0 < a < 1\) và \(m > n > 0\) thì \({a^m} < {a^n}\) để đánh giá \(A\) Lời giải chi tiết :
\(A = 1 - \dfrac{3}{4} + {\left( {\dfrac{3}{4}} \right)^2} - {\left( {\dfrac{3}{4}} \right)^3} + {\left( {\dfrac{3}{4}} \right)^4} - ... - {\left( {\dfrac{3}{4}} \right)^{2017}} + {\left( {\dfrac{3}{4}} \right)^{2018}}\) \( \Rightarrow \dfrac{3}{4}A = \dfrac{3}{4} - {\left( {\dfrac{3}{4}} \right)^2} + {\left( {\dfrac{3}{4}} \right)^3} - {\left( {\dfrac{3}{4}} \right)^4} + ...\) \( + {\left( {\dfrac{3}{4}} \right)^{2017}} - {\left( {\dfrac{3}{4}} \right)^{2018}} + {\left( {\dfrac{3}{4}} \right)^{2019}}\) \( \Rightarrow A + \dfrac{3}{4}A = 1 + {\left( {\dfrac{3}{4}} \right)^{2019}}\) \( \Rightarrow \left( {1 + \dfrac{3}{4}} \right)A = 1 + {\left( {\dfrac{3}{4}} \right)^{2019}}\) \( \Rightarrow \dfrac{7}{4}.A = 1 + {\left( {\dfrac{3}{4}} \right)^{2019}}\) \( \Rightarrow A = \left[ {1 + {{\left( {\dfrac{3}{4}} \right)}^{2019}}} \right]:\dfrac{7}{4} = \left[ {1 + {{\left( {\dfrac{3}{4}} \right)}^{2019}}} \right].\dfrac{4}{7}\) Suy ra \(A > 0\,\,\,\,\,\,\,\left( 1 \right)\) Vì \({\left( {\dfrac{3}{4}} \right)^{2019}} < \dfrac{3}{4} \Rightarrow A < \left( {1 + \dfrac{3}{4}} \right).\dfrac{4}{7} = 1\,\,\,\,\,\,\,\left( 2 \right)\) Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(0 < A < 1\). Vậy \(A\) không phải là số nguyên.
|














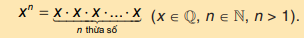





Danh sách bình luận