Trắc nghiệm Bài 1: Tập hợp Q các số hữu tỉ Toán 7 Cánh diềuĐề bài
Câu 1 :
Tập hợp số hữu tỉ được kí hiệu là
Câu 2 :
Chọn câu đúng
Câu 3 :
Số nào dưới đây là số hữu tỉ dương?
Câu 4 :
Số hữu tỉ là số được viết dưới dạng phân số \(\dfrac{a}{b}\) với:
Câu 5 :
Số \( - \dfrac{2}{3}\) được biểu diễn trên trục số bởi hình vẽ nào dưới đây?
Câu 6 :
Trong các phân số sau, phân số nào không bằng phân số $\dfrac{3}{4}$?
Câu 7 :
Cho các câu sau: (I) Số hữu tỉ dương lớn hơn số hữu tỉ âm (II) Số hữu tỉ dương lớn hơn số tự nhiên (III) Số $0$ là số hữu tỉ âm (IV) Số nguyên dương là số hữu tỉ. Số các câu đúng trong các câu trên là
Câu 8 :
Sắp xếp các số hữu tỉ sau theo thứ tự giảm dần: \(\dfrac{{ - 12}}{{17}};\dfrac{{ - 3}}{{17}};\dfrac{{ - 16}}{{17}};\dfrac{{ - 1}}{{17}};\dfrac{{ - 11}}{{17}};\dfrac{{ - 14}}{{17}};\dfrac{{ - 9}}{{17}}.\)
Câu 9 :
Số hữu tỉ lớn nhất trong các số \(\dfrac{7}{8};\dfrac{2}{3};\dfrac{3}{4};\dfrac{{18}}{{19}};\dfrac{{27}}{{28}}\) là:
Câu 10 :
So sánh hai số \(x = \dfrac{2}{{ - 5}}\) và \(y = \dfrac{{ - 3}}{{13}}\)
Câu 11 :
So sánh \(x = \dfrac{{2002}}{{2003}}\) và \(y = \dfrac{{14}}{{13}}\)
Câu 12 :
Biểu diễn các số: $\dfrac{1}{4}$; $0,25$; $\dfrac{{ - \,25}}{{ - 100}}$; $\dfrac{5}{{20}}$ bởi các điểm trên cùng một trục số ta được bao nhiêu điểm phân biệt?
Câu 13 :
Trong các phân số \(\dfrac{{14}}{{18}}\,\,;\,\,\dfrac{{24}}{{26}}\,\,;\,\,\dfrac{{26}}{{ - 28}}\,\,;\,\,\dfrac{{ - 28}}{{30}}\,\,;\,\,\dfrac{{72}}{{78}}\) có bao nhiêu phân số bằng phân số \(\dfrac{{12}}{{13}}\) ?
Câu 14 :
Cho số hữu tỉ \(x = \dfrac{{a - 3}}{2}.\) Với giá trị nào của $a$ thì $x$ là số nguyên dương;
Câu 15 :
Cho số hữu tỉ \(y = \dfrac{{2a - 1}}{{ - 3}}.\) Với giá trị nào của $a$ thì $y$ không là số dương và cũng không là số âm.
Câu 16 :
Số \(\dfrac{9}{4}\) có số đối là:
Câu 17 :
Khẳng định nào sau đây là đúng?
Câu 18 :
Trong các phân số sau, phân số nào biểu diễn số hữu tỉ -0,35
Câu 19 :
Biểu diễn các số: \( - 0,4;\frac{8}{{20}};\frac{{12}}{{ - 20}};\frac{{ - 3}}{8}; - 0,375\) bởi các điểm trên cùng một trục số ta được bao nhiêu điểm phân biệt?
Câu 20 :
Sắp xếp các số hữu tỉ \(\frac{{ - 7}}{{20}};\frac{5}{{ - 20}};\frac{{ - 5}}{{17}};\frac{1}{{ - 3}}\) theo thứ tự giảm dần:
Câu 21 :
Cho \(x = \frac{a}{{2{a^2} + 1}}\) Với giá trị nào của a thì x là số hữu tỉ dương?
Câu 22 :
Có mấy giá trị x nguyên thỏa mãn: \(\frac{{9}}{{ - 21}} > \frac{x}{7} > \frac{{ - 11}}{{14}}\)
Câu 23 :
Thành tích chạy thi 100 m của 4 bạn An, Bình, Chi, Duy lần lượt là: 21,54 giây; \(\frac{1}{3}\)phút; \(\frac{{108}}{5}\) giây; \(20\frac{3}{8}\) giây. Hỏi bạn nào chạy nhanh nhất?
Câu 24 :
Cho số hữu tỉ \(x = \frac{7}{{n + 2}}\) Tìm tổng của các số nguyên n sao cho x là một số nguyên
Lời giải và đáp án
Câu 1 :
Tập hợp số hữu tỉ được kí hiệu là
Đáp án : C Lời giải chi tiết :
Tập hợp các số hữu tỉ được kí hiệu là $Q.$ Tập hợp các số tự nhiên kí hiệu là $N.$ Tập hợp số tự nhiên khác $0$ kí hiệu là $N^*$
Câu 2 :
Chọn câu đúng
Đáp án : A Lời giải chi tiết :
Ta có \( - 6 \in \mathbb{Z};-6\notin\mathbb N \) nên D sai. \(\dfrac{2}{3} \in \mathbb{Q};\,\dfrac{2}{3} \notin \mathbb{Z}\) nên B sai. \( - \dfrac{9}{2} \in \mathbb{Q}\) nên C sai \(\dfrac{3}{2} \in \mathbb{Q}\) nên A đúng.
Câu 3 :
Số nào dưới đây là số hữu tỉ dương?
Đáp án : A Lời giải chi tiết :
\(\begin{array}{l}\dfrac{{ - 2}}{{ - 3}} = \dfrac{2}{3} > 0\,;\\\dfrac{{ - 2}}{5}\, < 0\,;\,\dfrac{{ - 5}}{{15}} < 0\,\,;\,\dfrac{2}{{ - 15}} < 0.\end{array}\) Vậy số hữu tỉ dương là \(\dfrac{{ - 2}}{{ - 3}}.\)
Câu 4 :
Số hữu tỉ là số được viết dưới dạng phân số \(\dfrac{a}{b}\) với:
Đáp án : B Lời giải chi tiết :
Số hữu tỉ là số được viết dưới dạng phân số \(\dfrac{a}{b}\) trong đó \(a,b \in Z\,;b \ne 0.\)
Câu 5 :
Số \( - \dfrac{2}{3}\) được biểu diễn trên trục số bởi hình vẽ nào dưới đây?
Đáp án : D Phương pháp giải :
Sử dụng cách biểu diễn số hữu tỉ trên trục số: Nếu \(\dfrac{-a}{b}\) là số hữu tỉ âm, ta chia khoảng có độ dài $1$ đơn vị làm $b$ phần bằng nhau, rồi lấy về phía chiều âm trục $Ox$ là $a$ phần , ta được vị trí của số \(\dfrac{-a}{b}\). Lời giải chi tiết :
Biểu diễn số \( - \dfrac{2}{3}\) trên trục số ta được: 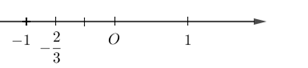 Chú ý
Một số em nhầm đáp án do không để ý rằng số \( - \dfrac{2}{3}\) phải nằm bên trái số \(0\).
Câu 6 :
Trong các phân số sau, phân số nào không bằng phân số $\dfrac{3}{4}$?
Đáp án : A Phương pháp giải :
Ta rút gọn các phân số rồi đưa các phân số về cùng mẫu số sau đó so sánh hai tử số với nhau. Lời giải chi tiết :
\(\dfrac{6}{9} = \dfrac{2}{3}\,;\,\dfrac{9}{{12}} = \dfrac{3}{4}\,;\,\dfrac{{ - 6}}{{ - 8}} = \dfrac{3}{4}\,;\,\dfrac{{ - 3}}{{ - 4}} = \dfrac{3}{4}.\) Vậy phân số không bằng phân số $\dfrac{3}{4}$ là \(\dfrac{6}{9}.\)
Câu 7 :
Cho các câu sau: (I) Số hữu tỉ dương lớn hơn số hữu tỉ âm (II) Số hữu tỉ dương lớn hơn số tự nhiên (III) Số $0$ là số hữu tỉ âm (IV) Số nguyên dương là số hữu tỉ. Số các câu đúng trong các câu trên là
Đáp án : B Lời giải chi tiết :
(I) đúng (II) sai vì số hữu tỉ dương chưa chắc lớn hơn số tự nhiên. Ví dụ: \(\dfrac{5}{4} < 2\) . (III) sai vì số 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm (IV) đúng vì mọi số nguyên dương đều là số hữu tỉ với mẫu số là \(1\). Vậy có hai câu đúng.
Câu 8 :
Sắp xếp các số hữu tỉ sau theo thứ tự giảm dần: \(\dfrac{{ - 12}}{{17}};\dfrac{{ - 3}}{{17}};\dfrac{{ - 16}}{{17}};\dfrac{{ - 1}}{{17}};\dfrac{{ - 11}}{{17}};\dfrac{{ - 14}}{{17}};\dfrac{{ - 9}}{{17}}.\)
Đáp án : C Phương pháp giải :
Để so sánh các số hữu tỉ có cùng mẫu ta so sánh các tử số với nhau. Phân số nào có tử số lớn hơn thì lớn hơn. Phân số nào có tử số nhỏ hơn thì nhỏ hơn. Lời giải chi tiết :
Vì \( - 1 > - 3 > - 9 > - 11 > - 12 > - 14 > - 16\) Nên ta có \(\dfrac{{ - 1}}{{17}} > \dfrac{{ - 3}}{{17}} > \dfrac{{ - 9}}{{17}} > \dfrac{{ - 11}}{{17}} > \dfrac{{ - 12}}{{17}} > \dfrac{{ - 14}}{{17}} > \dfrac{{ - 16}}{{17}}\) Vậy dãy số theo thứ tự giảm dần là \(\dfrac{{ - 1}}{{17}};\dfrac{{ - 3}}{{17}};\dfrac{{ - 9}}{{17}};\dfrac{{ - 11}}{{17}};\dfrac{{ - 12}}{{17}};\dfrac{{ - 14}}{{17}};\dfrac{{ - 16}}{{17}}\) Chú ý
Một số em nhầm đáp án D vì xếp theo thứ tự tăng dần. Ở đây đề bài yêu cầu thứ tự gảm dần.
Câu 9 :
Số hữu tỉ lớn nhất trong các số \(\dfrac{7}{8};\dfrac{2}{3};\dfrac{3}{4};\dfrac{{18}}{{19}};\dfrac{{27}}{{28}}\) là:
Đáp án : D Phương pháp giải :
So sánh các số hữu tỉ dựa vào phần bù với \(1\). Số nào có phần bù với \(1\) nhỏ nhất thì số đó lớn nhất. Lưu ý: Trong các phân số dương có cùng tử số dương, phân số nào có mẫu lớn hơn thì nhỏ hơn. Lời giải chi tiết :
Phần bù với \(1\) của các số \(\dfrac{7}{8};\dfrac{2}{3};\dfrac{3}{4};\dfrac{{18}}{{19}};\dfrac{{27}}{{28}}\) lần lượt là \(\dfrac{1}{8};\,\dfrac{1}{3};\dfrac{1}{4};\dfrac{1}{{19}};\dfrac{1}{{28}}\) Mà \(28 > 19 > 8 > 4 > 3\) nên \(\dfrac{1}{{28}} < \dfrac{1}{{19}} < \dfrac{1}{8} < \dfrac{1}{4} < \dfrac{1}{3}\) Suy ra \(\dfrac{{27}}{{28}} > \dfrac{{18}}{{19}} > \dfrac{7}{8} > \dfrac{3}{4} > \dfrac{2}{3}\) Số hữu tỉ lớn nhất là: \(\dfrac{{27}}{{28}}\)
Câu 10 :
So sánh hai số \(x = \dfrac{2}{{ - 5}}\) và \(y = \dfrac{{ - 3}}{{13}}\)
Đáp án : B Phương pháp giải :
Đưa hai phân số về cùng mẫu dương rồi so sánh hai tử số với nhau. Lời giải chi tiết :
Ta có \(x = \dfrac{2}{{ - 5}} = \dfrac{{2.\left( { - 13} \right)}}{{\left( { - 5} \right).\left( { - 13} \right)}} = \dfrac{{ - 26}}{{65}}\) và $y = \dfrac{{ - 3}}{{13}} = \dfrac{{ - 3.5}}{{13.5}} = \dfrac{{ - 15}}{{65}}$ Mà \( - 26 < - 15 \) suy ra \(\dfrac{{ - 26}}{{65}} < \dfrac{{ - 15}}{{65}}\) hay \(x < y\) .
Câu 11 :
So sánh \(x = \dfrac{{2002}}{{2003}}\) và \(y = \dfrac{{14}}{{13}}\)
Đáp án : C Phương pháp giải :
So sánh với số \(1\) Lời giải chi tiết :
Ta có \(x = \dfrac{{2002}}{{2003}} < \dfrac{{2003}}{{2003}} = 1\) hay \(x < 1\) Và \(y = \dfrac{{14}}{{13}} > \dfrac{{13}}{{13}} = 1\) hay \(y > 1\) Từ đó suy ra \(y > 1 > x\) hay \(y > x\) .
Câu 12 :
Biểu diễn các số: $\dfrac{1}{4}$; $0,25$; $\dfrac{{ - \,25}}{{ - 100}}$; $\dfrac{5}{{20}}$ bởi các điểm trên cùng một trục số ta được bao nhiêu điểm phân biệt?
Đáp án : A Phương pháp giải :
+ Rút gọn các phân số, đưa về cùng mẫu và so sánh các phân số + Sử dụng: Các số hữu tỉ bằng nhau được biểu diễn bởi cùng một điểm trên trục số. Lời giải chi tiết :
$0,25 = \dfrac{{25}}{{100}} = \dfrac{1}{4};\dfrac{{ - 25}}{{ - 100}} = \dfrac{1}{4};\dfrac{5}{{20}} = \dfrac{1}{4}.$ Nên \(\dfrac{1}{4} = 0,25 = \dfrac{{ - 25}}{{ - 100}} = \dfrac{5}{{20}}\) Do đó các số \(\dfrac{1}{4};0,25\,;\,\dfrac{{ - 25}}{{ - 100}}\,;\,\dfrac{5}{{20}}\) được biểu diễn cùng một điểm trên trục số. Chú ý
Một số em chưa so sánh các số mà kết luận luôn \(4\) điểm là sai.
Câu 13 :
Trong các phân số \(\dfrac{{14}}{{18}}\,\,;\,\,\dfrac{{24}}{{26}}\,\,;\,\,\dfrac{{26}}{{ - 28}}\,\,;\,\,\dfrac{{ - 28}}{{30}}\,\,;\,\,\dfrac{{72}}{{78}}\) có bao nhiêu phân số bằng phân số \(\dfrac{{12}}{{13}}\) ?
Đáp án : B Phương pháp giải :
Rút gọn các phân số sau đó so sánh các phân số đó với \(\dfrac{{12}}{{13}}\) . Lời giải chi tiết :
\(\dfrac{{14}}{{18}} = \dfrac{7}{9}\,;\,\dfrac{{24}}{{26}} = \dfrac{{12}}{{13}}\,\,;\,\dfrac{{72}}{{78}} = \dfrac{{12}}{{13}}.\) Ta có \(\dfrac{{26}}{{ - 28}} < 0 < \dfrac{{12}}{{13}};\,\dfrac{{ - 28}}{{30}} < 0 < \dfrac{{12}}{{13}}\) ; \(\dfrac{7}{9} = \dfrac{{91}}{{117}} < \dfrac{{108}}{{117}} = \dfrac{{12}}{{13}}\) Vậy có 2 phân số bằng phân số \(\dfrac{{12}}{{13}}\) là: \(\dfrac{{24}}{{26}}\,;\,\dfrac{{72}}{{78}}.\)
Câu 14 :
Cho số hữu tỉ \(x = \dfrac{{a - 3}}{2}.\) Với giá trị nào của $a$ thì $x$ là số nguyên dương;
Đáp án : D Phương pháp giải :
Số hữu tỉ \(\dfrac{a}{b}\) là số nguyên dương khi \(a,\,b\) cùng dấu và \(a \vdots b\). Lời giải chi tiết :
Để \(x = \dfrac{{a - 3}}{2}\) là số nguyên dương thì \(\left( {a - 3} \right) > 0\) và \(\left( {a - 3} \right) \vdots 2\) Giả sử \(a - 3 = 2k\,\left( {k \in {\mathbb{N}^*}} \right)\) suy ra \(a = 3 + 2k\,\left( {k \in {\mathbb{N}^*}} \right)\)
Câu 15 :
Cho số hữu tỉ \(y = \dfrac{{2a - 1}}{{ - 3}}.\) Với giá trị nào của $a$ thì $y$ không là số dương và cũng không là số âm.
Đáp án : B Phương pháp giải :
Số hữu tỉ \(0\) không là số dương cũng không là số âm. Nên ta cho $y=0$ từ đó tìm $a.$ Lời giải chi tiết :
Vì số hữu tỉ \(0\) không là số dương cũng không là số âm nên để \(y = \dfrac{{2a - 1}}{{ - 3}}\) không dương cũng không âm thì \(y = 0\) suy ra \(\dfrac{{2a - 1}}{{ - 3}} = 0\) nên \(2a - 1 = 0 \) do đó \(a = \dfrac{1}{2}\) .
Câu 16 :
Số \(\dfrac{9}{4}\) có số đối là:
Đáp án : C Phương pháp giải :
2 số đối nhau là 2 số có tổng bằng 0. Số đối của số hữu tỉ a là -a Lời giải chi tiết :
Số đối của \(\dfrac{9}{4}\) là \( - \dfrac{9}{4} = \dfrac{9}{{ - 4}}\)
Câu 17 :
Khẳng định nào sau đây là đúng?
Đáp án : C Phương pháp giải :
Tính chất, thứ tự trên tập hợp các só hữu tỉ Lời giải chi tiết :
+) Nếu a > b thì –a < -b nên A sai +) Nếu a < b, a < c thì chưa thể so sánh được b với c nên B sai +) Nếu a < b, c > b ( hay b < c) thì a < c ( tính chất bắc cầu) nên C đúng +) Số hữu tỉ gồm: số hữu tỉ âm, số hữu tỉ dương và số 0 nên D sai.
Câu 18 :
Trong các phân số sau, phân số nào biểu diễn số hữu tỉ -0,35
Đáp án : C Phương pháp giải :
Biểu diễn số thập phân dưới dạng phân số: + Viết số thập phân dưới dạng phân số có mẫu số là lũy thừa của 10 + Rút gọn phân số. Lời giải chi tiết :
Ta có: \( - 0,35 = \frac{{ - 35}}{{100}} = \frac{{( - 35):5}}{{100:5}} = \frac{{ - 7}}{{20}}\)
Câu 19 :
Biểu diễn các số: \( - 0,4;\frac{8}{{20}};\frac{{12}}{{ - 20}};\frac{{ - 3}}{8}; - 0,375\) bởi các điểm trên cùng một trục số ta được bao nhiêu điểm phân biệt?
Đáp án : B Phương pháp giải :
+ Đưa các số về dạng phân số tối giản rồi xác định các số bằng nhau. + Các số bằng nhau chỉ được biểu diễn bởi một điểm trên trục số. Lời giải chi tiết :
Ta có: \(\begin{array}{l} - 0,4 = \frac{{ - 4}}{{10}} = \frac{{ - 4:2}}{{10:2}} = \frac{{ - 2}}{5};\\\frac{8}{{20}} = \frac{{8:4}}{{20:4}} = \frac{2}{5};\\\frac{{12}}{{ - 20}} = \frac{{12:( - 4)}}{{( - 20):( - 4)}} = \frac{{ - 3}}{5};\\\frac{{ - 3}}{8};\\ - 0,375 = \frac{{ - 375}}{{1000}} = \frac{{( - 375):125}}{{1000:125}} = \frac{{ - 3}}{8}\end{array}\) Ta có các điểm biểu diễn khác nhau là \(\frac{{ - 2}}{5}; \frac{2}{5}; \frac{{ - 3}}{5}; \frac{{ - 3}}{8}\) Vậy các số trên biểu diễn 4 số hữu tỉ khác nhau nên được biểu diễn bởi 4 điểm khác nhau trên trục số
Câu 20 :
Sắp xếp các số hữu tỉ \(\frac{{ - 7}}{{20}};\frac{5}{{ - 20}};\frac{{ - 5}}{{17}};\frac{1}{{ - 3}}\) theo thứ tự giảm dần:
Đáp án : A Phương pháp giải :
+ Dùng tính chất: Nếu a < b thì –a > - b + Các phân số có cùng mẫu số dương: phân số nào có tử số lớn hơn thì phân số đó lớn hơn + Các phân số dương có cùng tử số: phân số nào có mẫu số lớn hơn thì nhỏ hơn Lời giải chi tiết :
+ So sánh \(\frac{5}{{ - 20}}\) và \( \frac{{ - 5}}{{17}}\): Vì 20 > 17 nên \(\frac{5}{{20}} < \frac{5}{{17}}\), do đó \(\frac{5}{{ - 20}} > \frac{{ - 5}}{{17}}\) + So sánh \(\frac{ - 5}{17}\) và \(\frac{1}{{ - 3}}\): Vì \(\frac{5}{{17}} < \frac{5}{{15}}\) nên \(\frac{{ - 5}}{{17}} > \frac{{ - 5}}{{15}} = \frac{1}{{ - 3}}\) + So sánh \(\frac{1}{ - 3}\) và \(\frac{{ - 7}}{{20}}\): Vì \(\frac{7}{{20}} > \frac{7}{{21}}\) nên \(\frac{{ - 7}}{{20}} < \frac{{ - 7}}{{21}} = \frac{1}{{ - 3}}\) Do đó, \(\frac{5}{{ - 20}} > \frac{{ - 5}}{{17}} > \frac{1}{{ - 3}} > \frac{{ - 7}}{{20}}\)
Câu 21 :
Cho \(x = \frac{a}{{2{a^2} + 1}}\) Với giá trị nào của a thì x là số hữu tỉ dương?
Đáp án : B Phương pháp giải :
Số hữu tỉ \(\frac{a}{b}\) là số hữu tỉ dương khi a, b cùng dấu Nhận xét về mẫu số của phân số Lời giải chi tiết :
\(x = \frac{a}{{2{a^2} + 1}}\) là số hữu tỉ dương thì \(x = \frac{a}{{2{a^2} + 1}} > 0\) Ta có: a2 \( \ge \)0, với mọi a nên 2a2 + 1 \( \ge \)1 > 0, với mọi a Như vậy, để \(x = \frac{a}{{2{a^2} + 1}}\) > 0 thì a > 0
Câu 22 :
Có mấy giá trị x nguyên thỏa mãn: \(\frac{{9}}{{ - 21}} > \frac{x}{7} > \frac{{ - 11}}{{14}}\)
Đáp án : B Phương pháp giải :
Đưa về các phân số có cùng mẫu số dương rồi so sánh tử số, suy ra điều kiện của x Lời giải chi tiết :
Ta có: \(\begin{array}{l}\frac{{9}}{{ - 21}} > \frac{x}{7} > \frac{{ - 11}}{{14}}\\ \frac{{ - 3}}{7} > \frac{x}{7} > \frac{{ - 11}}{{14}}\\ \frac{{ - 6}}{{14}} > \frac{{2x}}{{14}} > \frac{{ - 11}}{{14}}\\ - 6 > 2x > - 11\\ - 3 > x > - \frac{{11}}{2}\end{array}\) \( - 3 > x > - 5,5\) Mà x nguyên nên \(x \in \{ - 4; - 5\} \) Vậy có 2 giá trị x thỏa mãn
Câu 23 :
Thành tích chạy thi 100 m của 4 bạn An, Bình, Chi, Duy lần lượt là: 21,54 giây; \(\frac{1}{3}\)phút; \(\frac{{108}}{5}\) giây; \(20\frac{3}{8}\) giây. Hỏi bạn nào chạy nhanh nhất?
Đáp án : B Phương pháp giải :
So sánh thành tích của các bạn: So sánh các số hữu tỉ Bạn nào có thời gian chạy nhỏ nhất thì bạn đó chạy nhanh nhất. Lời giải chi tiết :
Ta có: \(\frac{1}{3}\)phút = \(\frac{1}{3}\) . 60 = 20 giây \(\frac{{108}}{5}\) giây = 21,6 giây \(20\frac{3}{8}\) giây = 20,375 giây Vì 20 < 20,375 < 21,54 < 21,6 nên Bình chạy nhanh nhất Chú ý
+ Đưa các số liệu về cùng đơn vị rồi mới so sánh + Nếu các số hữu tỉ viết được dưới dạng số thập phân thì ta viết chúng ở dạng số thập phân rồi so sánh.
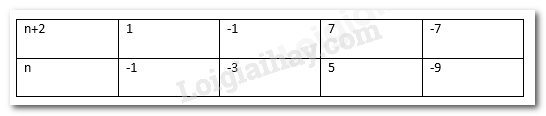
Câu 24 :
Cho số hữu tỉ \(x = \frac{7}{{n + 2}}\) Tìm tổng của các số nguyên n sao cho x là một số nguyên
Đáp án : D Phương pháp giải :
Để x là số nguyên thì \(7 \vdots (n + 2)\) hay \((n + 2) \in \) Ư (7) = {1; -1; 7; -7} Lời giải chi tiết :
Để x là số nguyên thì \(7 \vdots (n + 2)\) hay \((n + 2) \in \) Ư (7) = {1; -1; 7; -7} Ta có bảng sau:
Vậy có 4 giá trị n thỏa mãn điều kiện. Tổng của các giá trị n đó là: (-1) + (-3) + 5 + (-9) = -8
|




















Danh sách bình luận