Giải bài 6 trang 63 SGK Toán 7 tập 2 - Chân trời sáng tạo

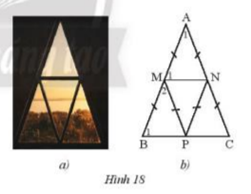
Đề bài

Một khung cửa sổ hình tam giác có thiết kế như Hình 18a được vẽ lại như Hình 18b.

a) Cho biết $\widehat {{A_1}}$$= {42^o}$. Tính số đo của $\widehat {{M_1}}$,$\widehat {{B_1}}$,$\widehat {{M_2}}$.

b) Chứng minh MN // BC, MP // AC.

c) Chứng minh bốn tam giác cân AMN, MBP, PMN, NPC bằng nhau.

Lời giải chi tiết

a)      Ta thấy tam giác AMN cân tại A do AM = AN

$\Rightarrow \widehat {{M_1}} = ({180^o} - \widehat {{A_1}}):2 = ({180^o} - {42^o}):2 = {69^o}$

Ta thấy tam giác PMN = tam giác AMN ( c-c-c )

$\Rightarrow \widehat {{M_1}} = \widehat {PMN} = {69^o}$ (góc tương ứng )

Mà $\Rightarrow \widehat {{M_1}} + \widehat {{M_2}} + \widehat {PMN} = {180^o}$( các góc kề bù )

$\Rightarrow \widehat {{M_2}} = {180^o} - {69^o} - {69^o} = {42^o}$

Mà tam giác MPB cân tại M do MB = MP nên

$\Rightarrow \widehat {{B_1}} = \widehat {MPB}$

Áp dụng định lí tổng 3 góc trong tam giác

$\Rightarrow \widehat {{B_1}} = ({180^o} - {42^o}):2 = {69^o}$

b)      Ta thấy $\widehat {{B_1}}$và $\widehat {{M_1}}$ở vị trí đồng vị và bằng nhau nên

$\Rightarrow$MN⫽BC

Vì tam giác PMN = tam giác AMN nên ta có

$\Rightarrow \widehat {{M_1}} = \widehat {ANM} = \widehat {PMN} = \widehat {MNP}$( do 2 tam giác cân và bằng nhau )

Mà $\widehat {MNA}$và$\widehat {PMN}$ ở vị trí so le trong

$\Rightarrow$MP⫽AC

c)      Ta có $\Delta AMN = \Delta PMN = \Delta MBP(c - g - c)$(1)

Vì MP⫽AC ( chứng minh trên )

$\Rightarrow \widehat {MPN} = \widehat {PNC}$ ( 2 góc so le trong ) =${42^o}$

$\Rightarrow \Delta MPN = \Delta NCP(c - g - c)$(2)

Từ (1) và (2) $\Rightarrow$ 4 tam giác cân AMN, MBP, PMN, NCP bằng nhau