Giải bài 3 trang 63 SGK Toán 7 tập 2 - Chân trời sáng tạoCho tam giác ABC cân tại A có Tổng hợp đề thi giữa kì 2 lớp 7 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - KHTN... Quảng cáo
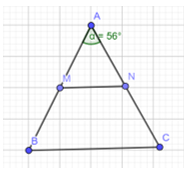
Đề bài Cho tam giác ABC cân tại A có \(\widehat A = {56^o}\)(Hình 15) a) Tính \(\widehat B\), \(\widehat C\) b) Gọi M, N lần lượt là trung điểm của AB, AC. Chứng minh rằng tam giác AMN cân. c) Chứng minh rằng MN // BC
Video hướng dẫn giải Phương pháp giải - Xem chi tiết a) Sử dụng định lí tổng 3 góc trong tam giác và tính chất 2 góc đáy tam giác cân b) Chứng minh AM = AN c) Sử dụng tính chất góc đồng vị Lời giải chi tiết a) Theo đề bài ta có tam giác ABC cân ở A và \(\widehat A = {56^o}\) Mà \( \widehat A + \widehat B + \widehat C = {180^o}\) nên \(\widehat B = \widehat C = ({180^o} - {56^o}):2 = {62^o}\) b) Vì tam giác ABC cân tại A nên AB = AC (định nghĩa tam giác cân) Mà M, N là trung điểm của AB, AC Nên AM = AN Xét tam giác AMN có AM = AN nên AMN là tam giác cân tại A suy ra \(\widehat M = \widehat N = ({180^o} - {56^o}):2 = {62^o}\) c) Vì \(\widehat {AMN}=\widehat {ABC}\) (cùng bằng 62°) Mà chúng ở vị trí đồng vị nên MN⫽BC
|




















Danh sách bình luận