Bài 23 trang 87 SBT toán 6 tập 2

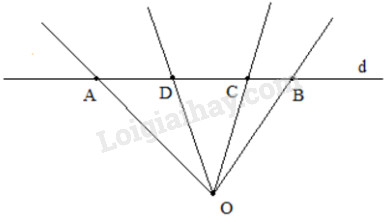
Đề bài

Trên đường thẳng \(d\) từ trái sang phải ta lấy các điểm \(A, D, C, B\) và lấy điểm \(O\) nằm ngoài đường thẳng \(d\). Biết \(\widehat {AO{\rm{D}}} = {30^o},\widehat {DOC} = {40^o},\widehat {AOB} = {90^o}.\) Tính \(\widehat {AOC},\widehat {COB},\widehat {DOB}.\)

Lời giải chi tiết

Vì \(D\) nằm giữa \(A\) và \(C\) nên tia \(OD\) nằm giữa hai tia \(OA\) và \(OC\), suy ra :

\(\widehat {AO{{D}}} + \widehat {DOC} = \widehat {AOC}\)

Thay \(\widehat {AO{{D}}} = {30^o};\widehat {DOC} = {40^o}\) ta có:

\(\widehat {AOC} = {30^o} + {40^o} = {70^o}\)

Vì \(C\) nằm giữa \(A\) và \(B\) nên tia \(OC\) nằm giữa hai tia \(OA\) và \(OB\), suy ra:

\(\widehat {AOC} + \widehat {COB} = \widehat {AOB}\)

Thay \(\widehat {AOC} = {70^o};\widehat {AOB} = {90^o}\) ta có:

\({70^o} + \widehat {COB} = {90^o}\)

\( \Rightarrow \widehat {COB} = {90^o} - {70^o} = {20^o}\)

Vì \(D\) nằm giữa \(A\) và \(B\) nên tia \(OD\) nằm giữa hai tia \(OA\) và \(OB\) nên:

\(\widehat {AO{{D}}} + \widehat {DOB} = \widehat {AOB}\)

Thay \(\widehat {AOD} = {30^o};\widehat {AOB} = {90^o}\) ta có:

\({30^o} + \widehat {DOB} = {90^o} \)

\(\Rightarrow \widehat {DOB} = {90^o} - {30^o} = {60^o}\)

Loigiaihay.com