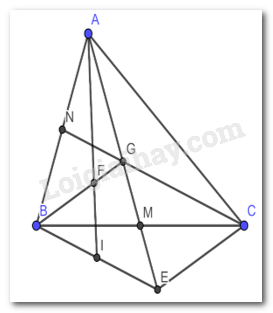
Giải bài 3 trang 75 SGK Toán 7 tập 2 - Chân trời sáng tạo

Đề bài

Cho tam giác ABC. Hai đường trung tuyến AM và CN cắt nhau tại G. Trên tia đối của tia AM lấy điểm E sao cho ME = MG.

a) Chứng minh rằng BG song song với EC.

b) Gọi I là trung điểm của BE, AI cắt BG tại F. Chứng minh rằng AF = 2FI

Lời giải chi tiết

a) Xét tam giác BGM và tam giác CEM có :

\(\widehat {GMB} = \widehat {EMC}\)(2 góc đối đỉnh)

GM = ME (do G đối xứng E qua M)

MB = MC (do M là trung điểm của BC)

\( \Rightarrow \Delta BGM = \Delta CEM(c - g - c)\)

\( \Rightarrow \widehat {GBM} = \widehat {MCE}\)(2 góc tương ứng bằng nhau)

Mà 2 góc trên ở vị trí so le trong nên BG⫽CE

b) Vì I là trung điểm BE nên AI sẽ là trung tuyến của tam giác ABE

Và BG cũng là trung tuyến của tam giác ABE do G là trung điểm AE

Vì BG cắt AI tại F nên F sẽ là trọng tâm của tam giác ABE

\(\, \Rightarrow AF = \dfrac{2}{3}AI\)(định lí về trọng tâm tam giác)

Mà AI = AF + FI \( \Rightarrow \) FI = AI – AF

\( \Rightarrow FI = AI - \dfrac{2}{3}AI = \dfrac{1}{3}AI\)

\( \Rightarrow 2FI = AF = \dfrac{2}{3}AI\)

\( \Rightarrow \) AF = 2 FI