Giải mục 2 trang 7,8,9 SGK Toán 7 tập 2 - Chân trời sáng tạo

HĐ 4

Các bạn Bình, Mai và Lan cùng thi giải nhanh các bài toán trong sách Bài tập Toán 7. Trong một giờ, số bài làm được của mỗi bạn lần lượt là 4;3;5. Cô giáo thưởng cho mỗi bạn số hình dán lần lượt là 8;6;10. Hãy so sánh tỉ số giữa số hình dán được thưởng và số bài toán làm được của mỗi bạn

Phương pháp giải:

• Xác định số bài làm và số hình dán được thưởng của mỗi bạn là bao nhiêu
• Tính tỉ số giữa số bài tập và số hình dán của mỗi bạn
• So sánh tỉ số giữa hình dán và bài tập làm được của mỗi bạn

Lời giải chi tiết:

Tỉ số giữa số bài làm được và số hình dán được thưởng của bạn Bình là : \(\dfrac{3}{6} = \dfrac{1}{2}\)

Tỉ số giữa số bài làm được và số hình dán được thưởng của bạn Mai là : \(\dfrac{3}{6} = \dfrac{1}{2}\)

Tỉ số giữa số bài làm được và số hình dán được thưởng của bạn Lan là : \(\dfrac{5}{{10}} = \dfrac{1}{2}\)

Sau khi rút gọn ta thấy tỉ số giữa số bài làm được và hình dán được thưởng của mỗi bạn đều bằng nhau và cùng bằng \(\dfrac{1}{2}\)

Thực hành 3

Cho biết ba số a,b,c tỉ lệ với các số 2;4;6. Hãy ghi dãy tỉ số bằng nhau tương ứng

Phương pháp giải:

• Lập các phân số là những tỉ số tương ứng
• Lập dãy tỉ số bằng nhau từ những tỉ số đã lập được

Lời giải chi tiết:

Theo đề bài các số a, b, c tỉ lệ với các số 2, 4, 6

\( \Rightarrow \) a : b : c = 2 : 4 : 6

\( \Rightarrow \) \(\dfrac{a}{2} = \dfrac{b}{4} = \dfrac{c}{6}\) ( Áp dụng lí thuyết về dãy tỉ số bằng nhau )

Vận dụng 3

Gọi m,n,p,q là số quyển vở được chia của bốn bạn Mai, Ngọc, Phú, Quang. Cho biết số điểm 10 đạt được của bốn bạn lần lượt là 12;13;14;15 và số quyển vở được chia tỉ lệ với số điểm 10. Hãy viết dãy tỉ số bằng nhau tương ứng.

Phương pháp giải:

• Lập các tỉ số giữa số quyển vở và số điểm 10 của mỗi bạn tương ứng
• Lập dãy tỉ số bằng nhau từ các tỉ số vừa lập được

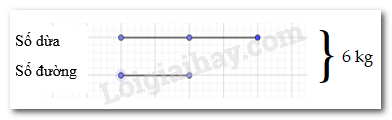
Lời giải chi tiết:

Tỉ số giữa số quyển vở và số điểm 10 của bạn Mai là : \(\dfrac{m}{{12}}\)

Tỉ số giữa số quyển vở và số điểm 10 của bạn Ngọc là : \(\dfrac{n}{{13}}\)

Tỉ số giữa số quyển vở và số điểm 10 của bạn Phú là : \(\dfrac{p}{{14}}\)

Tỉ số giữa số quyển vở và số điểm 10 của bạn Quang là : \(\dfrac{q}{{15}}\)

Từ các tỉ số trên ta lập được dãy tỉ số bằng nhau : \(\dfrac{m}{{12}} = \dfrac{n}{{13}} = \dfrac{p}{{14}} = \dfrac{q}{{15}}\)

HĐ 5

Cho tỉ lệ thức \(\dfrac{3}{7} = \dfrac{9}{{21}}\). Hãy tính các tỉ số \(\dfrac{{3 + 9}}{{7 + 21}}\) và \(\dfrac{{3 - 9}}{{7 - 21}}\) rồi so sánh chúng với các tỉ số trong tỉ lệ thức đã cho.

Phương pháp giải:

Lần lượt thực hiện và tối giản các phép tính

Từ kết quả thu được và so sánh chúng với các tỉ số trong tỉ lệ đã cho

Lời giải chi tiết:

Ta có tỉ thức : \(\dfrac{3}{7} = \dfrac{9}{{21}}\)

Xét \(\dfrac{{3 + 9}}{{7 + 21}}\) = \(\dfrac{{12}}{{28}}\) = \( = \dfrac{3}{7}\)( chia cả tử và mẫu cho 4 )

Xét \(\dfrac{{3 - 9}}{{7 - 21}}\) = \(\dfrac{{ - 6}}{{ - 14}}\)\( = \dfrac{3}{7}\)( chia cả tử và mẫu cho 2 )

Sau khi thực hiện tính các tỉ số ta thấy các kết quả sau khi tối giản của tỉ số bằng với các tỉ số trong tỉ lệ thức đã cho .

Thực hành 4

Tìm hai số x, y biết rằng:

a)      x + y = 30 và \(\dfrac{x}{2}\)= \(\dfrac{y}{3}\)

b)      x – y = −21 và \(\dfrac{x}{5}\)= \(\dfrac{y}{{ - 2}}\)

Phương pháp giải:

Áp dụng tính chất \(\dfrac{a}{b} = \dfrac{c}{d} = \dfrac{{a \pm c}}{{b \pm d}}\)

Lời giải chi tiết:

a)      \(x + y = 30;\dfrac{x}{2} = \dfrac{y}{3}\) áp dụng tính chất của tỉ lệ thức ra có :

\( \Rightarrow \dfrac{{x + y}}{{2 + 3}} = \dfrac{x}{2}\)

\( \Rightarrow \dfrac{{30}}{5} = \dfrac{x}{2}\)

\( \Rightarrow 30.2 = x.5\)

\( \Rightarrow 60:5 = x\\ \Rightarrow x = 12\)

\(\Rightarrow 14 + y = 30\) (thay x vừa tìm được = 12 vào x + y = 30 để tìm ra y)

\(\Rightarrow y = 18\)    

Vậy x = 12 y = 18

b)      Ta có : \(\dfrac{x}{5} = \dfrac{y}{{ - 2}}\)= \(\dfrac{{x - y}}{{5 + 2}}\)( áp dụng tính chất tỉ lệ thức ) (1)

Mà theo đề bài x – y = -21

Thay -21 vào (1) ta có : \(\dfrac{{ - 21}}{7} =  - 3\) \( = \dfrac{x}{5}\)

\( \Rightarrow \)x = (-3).5

\( \Rightarrow \)x = -15

Thay x bằng -15 ta có -15 – y = -21

\( \Rightarrow \)y = -15 + 21

\( \Rightarrow \)y = 6

Vậy x = -15 và y = 6

Vận dụng 4

a) Nguyên liệu của món mứt dừa sau khi hoàn thành chỉ gồm dừa và đường theo tỷ lệ 2 : 1. Tính xem trong 6 kg mứt dừa có bao nhiêu ki-lô-gam dừa và bao nhiêu ki-lô-gam đường.

 b) Bạn Dũng và bạn Thủy muốn làm mứt gừng theo công thức: Cứ 3 phần gừng thì cần 2 phần đường. Hai bạn mua 600g gừng.  Hai bạn cần mua bao nhiêu gam đường?

  c) Mẹ chỉ có 10 quyển vở, số vở chia cho hai chị em An và Bình. Tính số sách chia cho mỗi em, biết rằng số tuổi của An và Bình là 8; 12 và số sách tỉ lệ thuận với số tuổi

Phương pháp giải:

a)      Theo tỉ lệ 2:1 thì trong 6kg mứt dừa sẽ có 3 phần nguyên liệu bằng nhau trong đó 2 phần là dừa còn lại là đường .

b)      Từ số phần gừng và đường ta suy ra được tỉ lệ của gừng và đường . Sau đó lấy tỉ lệ nhân với số gừng đã mua để ra só đường cần mua .

c)      Tính tỉ lệ quyển vở của 2 chị em và vì An nhỏ tuổi hơn nên tỉ lệ của An thấp hơn. Sau đó rút gọn tỉ lệ để tìm được số vở của mỗi người dựa vào số vở đã cho có ở đầu bài.

Lời giải chi tiết:

a)      Tỉ lệ dừa và đường là : \(\dfrac{2}{1}\)

Ta có sơ đồ sau :

\( \Rightarrow \) Số kg đường là : 6 : ( 2+1) = 2 (kg) ( Áp dụng bài toán tổng tỉ đã học ở tiểu học )

\( \Rightarrow \) Số kg dừa là : 2 . 2 = 4 (kg)

b)      Tỉ lệ của gừng và đường là 3:2 ta có được tỉ số giữa gừng và đường là  \(\dfrac{3}{2}\) nên số đường bằng \(\dfrac{2}{3}\) số gừng.

Theo đề bài hai bạn đã mua 600 g gừng nên

\( \Rightarrow \) Số đường cần mua là : \(\dfrac{2}{3} \times 600\)= 400 g

Vậy 2 bạn cần mua 400g đường

c)      Ta có số tuổi của An và Bình lần lượt là 8;12 nên ta sẽ có tỉ số tuổi của 2 bạn là  \(\dfrac{8}{{12}} = \dfrac{2}{3}\)

Vậy số sách của An và Bình sẽ có tỉ số là 2:3

Theo đề bài chị Chi có 10 quyển vở mà theo tỉ số vừa tính được trong số 10 quyển vở đó An có 2 phần và Bình có 3 phần .

\( \Rightarrow \) Số vở của An là 10 : ( 2+3) . 2 = 4 quyển vở ( Áp dụng bài toán tổng tỉ đã được học ở lớp dưới )

\( \Rightarrow \) Số vở của Bình là : 10 – 4 = 6 quyển vở .

Thực hành 5

Tìm ba số x, y, z, biết x + y + z = 100 và x : y : z = 2 : 3 : 5

Phương pháp giải:

• Từ những tỉ số đề bài cho ta lập được các dãy tỉ số bằng nhau từ tính chất dãy tỉ số bằng nhau .
• Sau khi lập được dãy tỉ số bằng nhau thì thay số lần lượt vào các tỉ số để tìm được x, y, z .

Lời giải chi tiết:

Từ dãy x : y : z = 2 : 3 : 5 ta có : \(\dfrac{x}{2} = \dfrac{y}{3} = \dfrac{z}{5}\)

Mà theo đề bài x + y + z = 100

Áp dụng tính chất dãy tỉ số bằng nhau, ta được:

\(\dfrac{x}{2} = \dfrac{y}{3} = \dfrac{z}{5}=\dfrac{{x + y + z}}{{2 + 3 + 5}} = \dfrac{{100}}{{10}} = 10\)

\( \Rightarrow \) 10 \( = \dfrac{x}{2}\)\( \Rightarrow \) x = 10.2 = 20  

\( \Rightarrow \) 10 \( = \dfrac{y}{3}\) \( \Rightarrow \) y = 10.3 = 30

\( \Rightarrow \) 10 \( = \dfrac{z}{5}\) \( \Rightarrow \) z = 10.5 = 50    

Vận dụng 5

Hãy giải bài toán tiền lãi ở hoạt động khởi động (trang 6)

Đầu năm, các bác Xuân, Yến, Dũng góp vốn làm ăn với số tiền lần lượt là 300 triệu đồng, 400 triệu đồng và 500 triệu đồng . Tiền lãi thu được sau một năm là 240 triệu đồng . Hãy tìm số tiền lãi mỗi bác được chia, biết rằng tiền lãi được chia tỉ lệ với số tiền đã góp .

Phương pháp giải:

• Tìm tỉ lệ số vốn mỗi người góp ban đầu .
• Dựa vào tỉ lệ số vốn mỗi người góp ban đầu sẽ tương ứng với tỉ lệ lãi của mỗi người .

Lời giải chi tiết:

Tổng số vốn của 3 bác Xuân, Yến, Dũng là : 300 + 400 + 500 = 1200 triệu đồng .

Tỉ lệ vốn của bác Xuân là : \(\dfrac{{300}}{{1200}}\)\( = \dfrac{1}{4}\)

TỈ lệ góp vốn của bác Yến là : \(\dfrac{{400}}{{1200}}\)\( = \dfrac{1}{3}\)

Tỉ lệ góp vốn của bác Dũng là  : \(\dfrac{{500}}{{1200}}\) \( = \dfrac{5}{{12}}\)

Từ các tỉ lệ góp vốn trên ta tính được tỉ lệ lãi của mỗi người theo số vốn là :

Bác Xuân có số lãi là : \(\dfrac{1}{4} \times 240\)= 60 ( triệu đồng )

Bác Yến có số lãi là : \(\dfrac{1}{3} \times 240\)= 80 ( triệu đồng )

Bác Dũng có số lãi là : 240 – 80 -  60 = 100 ( triệu đồng )