Giải mục 2 trang 74 SGK Toán 7 tập 1 - Chân trời sáng tạo

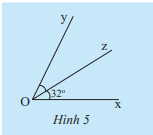
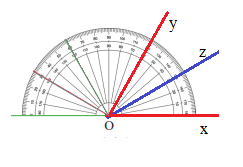
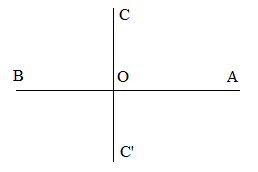
HĐ 2

Trong Hình 5, nếu tia Oz là tia phân giác của \(\widehat {xOy}\) thì số đo của \(\widehat {xOy}\) bằng bao nhiêu?

Phương pháp giải:

Nếu tia Oz là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOz} = \widehat {zOy}\) và \(\widehat {xOy} = \widehat {xOz} + \widehat {zOy}\)

Lời giải chi tiết:

Vì tia Oz là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOz} = \widehat {zOy}\) và \(\widehat {xOy} = \widehat {xOz} + \widehat {zOy}\)

Như vậy, \(\widehat {yOz} = \widehat {xOz} = 32^\circ \) nên \(\widehat {xOy} = \widehat {xOz} + \widehat {zOy}\) = \(32^\circ  + 32^\circ  = 64^\circ \)

Chú ý: 

Nếu tia Oz là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy}\)

Thực hành 2

Vẽ một góc có số đo bằng 60 \(^\circ \) rồi vẽ tia phân giác của góc đó.

Phương pháp giải:

Vẽ tia phân giác Oz của góc xOy

Bước 1: Vẽ góc \(\widehat {xOy} = 60^\circ \). Ta có: \(\widehat {xOz} = \widehat {zOy}\) và \(\widehat {xOy} = \widehat {xOz} + \widehat {zOy}\) nên \(\widehat {xOz} = \frac{{60^\circ }}{2} = 30^\circ \)

Bước 2: Dùng thước đo góc vẽ tia Oz đi qua một điểm trong của \(\widehat {xOy}\)sao cho \(\widehat {xOz} = 30^\circ \)

Ta được Oz là tia phân giác của góc xOy

Lời giải chi tiết:

Vận dụng 2

Hãy vẽ một góc bẹt \(\widehat {AOB}\) rồi vẽ tia phân giác của góc đó.

Phương pháp giải:

Vẽ tia phân giác của góc bẹt

Bước 1: Vẽ góc bẹt \(\widehat {AOB}\) .  Ta có: \(\widehat {AOC} = \widehat {COB}\) và \(\widehat {AOB} = \widehat {AOC} + \widehat {COB}\) nên \(\widehat {AOC} = 90^\circ \)

Bước 2: Cách 1: Dùng thước đo góc vẽ tia OC đi qua điểm C nằm trong \(\widehat {AOB}\)sao cho \(\widehat {AOC} = 90^\circ \)

Cách 2: Dùng eke kẻ OC vuông góc với OA

Ta được OC là tia phân giác của góc \(\widehat {AOB}\)

Lời giải chi tiết:

Chú ý: Góc bẹt có 2 tia phân giác là 2 tia đối nhau