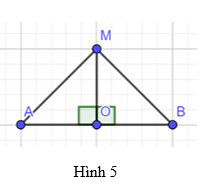
Giải mục 2 trang 68, 69 SGK Toán 7 tập 2 - Chân trời sáng tạoCho đoạn thẳng AB có O là trung điểm và d là đường trung trực. Lấy điểm M tùy ý thuộc d (Hình 5). Chứng minh rằng hai tam giác MOA và MOB bằng nhau, từ đó suy ra MA = MB Quảng cáo
Video hướng dẫn giải HĐ 2 Cho đoạn thẳng AB có O là trung điểm và d là đường trung trực. Lấy điểm M tùy ý thuộc d (Hình 5). Chứng minh rằng hai tam giác MOA và MOB bằng nhau, từ đó suy ra MA = MB
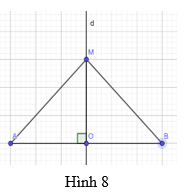
Phương pháp giải: - Chứng minh 2 tam giác bằng nhau (c-g-c) - Từ đó suy ra các cặp cạnh tương ứng bằng nhau Lời giải chi tiết: Theo giả thiết ta có O là trung điểm AB \( \Rightarrow \) AO = OB Xét tam giác AOM và tam giác BOM có : OM là cạnh chung AO = OB \(\widehat {MOA} = \widehat {MOB} = {90^o}\)( do d là trung trực AB ) (c-g-c) \( \Rightarrow MA = MB\) ( cạnh tương ứng ) Thực hành 2 Trong Hình 8, cho biết d là đường trung trực của đoạn thẳng AB, điểm M thuộc đường thẳng d, MA = x + 2 và MB = 7. Tính x
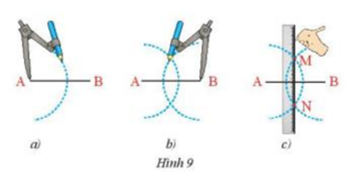
Phương pháp giải: - Sử dụng tính chất điểm thuộc trung trực của 1 đoạn thẳng cách đều 2 đầu mút Lời giải chi tiết: Vì M thuộc trung trực của AB \( \Rightarrow \) MA = MB \( \Rightarrow \) 7 = x + 2 \( \Rightarrow \) x = 5 Vận dụng 2 Dựng đường trung trực của đoạn thẳng AB bằng thước thẳng và compa theo hướng dẫn sau: - Lấy A làm tâm vẽ cung tròn bán kính lớn hơn \(\dfrac{1}{2}\)AB (Hình 9a) - Lấy B làm tâm vẽ cung tròn có bán kính bằng bán kính ở trên (Hình 9b) - Hai cung tròn này cắt nhau tại M và N (Hình 9c). Dùng thước vẽ đường thẳng MN. Hãy chứng minh đường thẳng MN chính là đường trung trực của đoạn thẳng AB.
Phương pháp giải: Chứng minh M, N cùng thuộc trung trực của AB Lời giải chi tiết: Vì 2 cung tròn cắt nhau tại M nên AM = MB = bán kính cung tròn Chứng minh tương tự \( \Rightarrow \) AN = BN = bán kính cung tròn \( \Rightarrow \) Vì M, N cách đều 2 đầu mút của đoạn AB nên M, N thuộc trung trực của AB Và chỉ có 1 đường thẳng đi qua 2 điểm nên MN là trung trực của AB
|




















Danh sách bình luận