Giải bài 4 trang 70, 71 vở thực hành Toán 7 tập 2Cho tam giác ABC. D là một điểm bất kì trên đoạn BC. Từ B, C kẻ các đường vuông góc BK, CN đến đường thẳng AD. a) So sánh BK, BD. b) So sánh (BK + CN) với BC. c) Chứng minh (BK + CN < frac{1}{2}left( {AB + BC + CA} right)). Quảng cáo
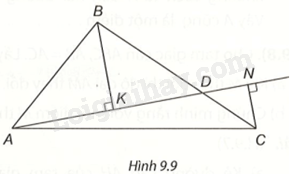
Đề bài Cho tam giác ABC. D là một điểm bất kì trên đoạn BC. Từ B, C kẻ các đường vuông góc BK, CN đến đường thẳng AD. a) So sánh BK, BD. b) So sánh \(BK + CN\) với BC. c) Chứng minh \(BK + CN < \frac{1}{2}\left( {AB + BC + CA} \right)\). Phương pháp giải - Xem chi tiết a) Tam giác vuông BKD có BD là cạnh huyền nên \(BK < BD\). b) + Từ a) suy ra \(BK + CN < BD + CN\). + Chứng minh tương tự: \(BD + CN < BD + CD\). Do đó, \(BK + CN < BD + CN < BD + CD = BC\). c) + Chứng minh \(BK < AB\), \(CN < AC\). + Mà \(BK + CN < BC\) nên \(\left( {BK + CN} \right) + BK + CN < BC + AB + AC\), nên \(BK + CN < \frac{1}{2}\left( {AB + BC + CA} \right)\) Lời giải chi tiết
a) Trong tam giác vuông BKD có BD là cạnh huyền nên \(BK < BD\) (1) b) Từ (1) suy ra \(BK + CN < BD + CN\) (2) Trong tam giác vuông CND có DC là cạnh huyền nên \(NC < CD\), suy ra: \(BD + CN < BD + CD\). (3) Từ (2) và (3) suy ra \(BK + CN < BD + CN < BD + CD = BC\). Do đó, \(BK + CN < BC\). (4) c) Trong tam giác vuông ABK có AB là cạnh huyền nên \(BK < AB\). (5) Trong tam giác vuông CAN có AC là cạnh huyền nên \(CN < AC\). (6) Từ (4), (5) và (6) suy ra \(\left( {BK + CN} \right) + BK + CN < BC + AB + AC\), hay \(2\left( {BK + CN} \right) < AB + BC + CA\), do đó \(BK + CN < \frac{1}{2}\left( {AB + BC + CA} \right)\).
|




















Danh sách bình luận