Bài 32 trang 91 SBT toán 6 tập 2

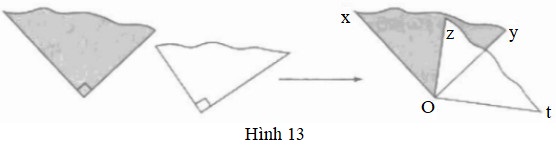
Đề bài

a) Cắt hai góc vuông rồi đặt lên nhau như hình 13.

b) Vì sao có \(\widehat {xOz} = \widehat {y{{O}}t}\) ?

c) Vì sao tia phân giác của \(\widehat {y{{O}}z}\) cũng là tia phân giác của \(\widehat {xOt}\) ?

Lời giải chi tiết

a) Học sinh tự thực hành

b) Vì \(\widehat {xOy} = \widehat {tOz} = {90^o},\) phần chồng lên nhau là \(\widehat {zOy}\) 

Ta có: 

\(\begin{array}{l}
\widehat {xOz} = \widehat {xOy} - \widehat {yOz} = {90^0} - \widehat {yOz}\\
\widehat {yOt} = \widehat {tOz} - \widehat {yOz} = {90^0} - \widehat {yOz}
\end{array}\)

Suy ra: \(\widehat {xOz} = \widehat {y{{Ot}}}\)

c) Gọi \(Ot’\) là tia phân giác của \(\widehat {zOy}\)

\(\displaystyle  \Rightarrow \widehat {zOt'} = \widehat {t'Oy} = {{\widehat {zOy}} \over 2}\)

Mà \(\widehat {xOz} = \widehat {y{{Ot}}}\) (theo câu b) 

Suy ra \(\widehat {xOz} + \widehat {zOt'} = \widehat {t'Oy} + \widehat {y{\rm{O}}t}\)

Hay \(\widehat {xOt'} = \widehat {t'Ot}\).

Vậy \(Ot’\) là tia phân giác \(\widehat {xOt}\).

Loigiaihay.com