Giải bài 2 trang 66 SGK Toán 7 tập 2 - Chân trời sáng tạo

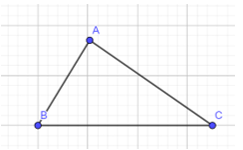
Đề bài

Cho tam giác ABC có $\widehat A =$${100^0}$,$\widehat B$$= {40^o}$.

a) Tìm cạnh lớn nhất của tam giác ABC.

b) Tam giác ABC là tam giác gì? Vì sao?

Lời giải chi tiết

a) Do $\widehat{A}=100^0>90^0$ nên là góc tù, do đó, $\widehat{A}$ là góc lớn nhất trong tam giác ABC.

$\Rightarrow$ BC là cạnh lớn nhất của tam giác ABC (do BC đối diện với góc A trong tam giác ABC)

b) 

Theo định lí tổng 3 góc trong tam giác ABC, ta có:

$\Rightarrow \widehat A + \widehat B + \widehat C = {180^o}$

$\Rightarrow \widehat C = {180^o} - {100^o} - {40^o} = {40^o}$

 $\Rightarrow\widehat C = \widehat B = {40^o}$

$\Rightarrow$ ABC là tam giác cân tại A.