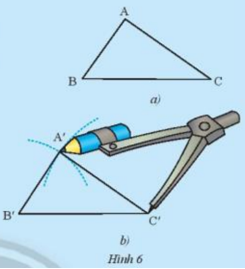
Giải mục 2 trang 49, 50, 51, 52, 53, 54 SGK Toán 7 tập 2 - Chân trời sáng tạo

HĐ 2

Cho tam giác ABC như trong Hình 6a. Lấy một tờ giấy, trên đó vẽ tam giác A’B’C’có ba cạnh bằng ba cạnh của tam giác ABC (A’B’= AB, A’C’= AC, B’C’= BC) theo các bước:

-Vẽ đoạn thẳng B’C’= BC

-Vẽ cung tròn tâm B’có bán kính bằng BA, vẽ cung trong tâm C’ có bán kính bằng CA.

-Hai cung tròn trên cắt nhau tại A’ (chỉ lấy một trong hai giao điểm của hai cung)

-Vẽ các đoạn thẳng B’A, C’A’, ta được tam giác A’B’C’ (Hình 6b)

Em hãy cắt rời tam giác A’B’C’ ra khỏi tờ giấy vừa vẽ và thử xem có thể đặt chồng khít tam giác A’B’C’ lên tam giác ABC hay không.

Theo em, hai tam giác ABC và A’B’C’ trong trường hợp này có bằng nhau hay không?

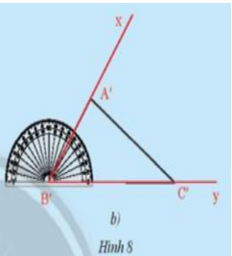
Phương pháp giải:

Vẽ hình và so sánh độ dài các cạnh các góc của 2 tam giác

Lời giải chi tiết:

Xét tam giác ABC và tam giác A’B’C’ có :

BC = B’C’ ( giả thiết )

B’A’ = BA

A’C’ = CA

Hai tam giác có thể đặt chồng khít lên nhau nên 2 tam giác bằng nhau

HĐ 3

Cho tam giác ABC như trong Hình 8a. Lấy một tờ giấy, trên đó vẽ tam giác A’B’C’có \(\widehat {B'} = \widehat B\), B’A’ = BA, B’C’ = BC theo các bước:

- Vẽ \(\widehat {xB'y} = \widehat {ABC}\)

- Trên tia B’x lấy đoạn B’A’= BA.

- Trên tia B’y lấy đoạn B’C’ = BC.

-Vẽ đoạn A’C’, ta được tam giác A’B’C’(Hình 8b)

Em hãy cắt rời tam giác A’B’C’ra khỏi tờ giấy vừa vẽ và thử xem có thể đặt chồng khít tam giác A’B’C’lên tam giác ABC hay không.

Theo em, hai tam giác ABC và A’B’C’ trong trường hợp này có bằng nhau hay không? 

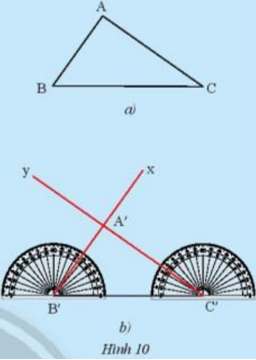
Phương pháp giải:

- Vẽ góc trước rồi vẽ 2 cạnh theo đề bài

- Cắt giấy theo hình vẽ được

- So sánh hai tam giác xem chúng bằng nhau hay không

Lời giải chi tiết:

Ta thấy 2 tam giác có thể chồng khít lên nhau nên 2 tam giác bằng nhau.

Chú ý: 2 tam giác bằng nhau khi có 2 cặp cạnh bằng nhau và góc xen giữa 2 cặp cạnh đó cũng bằng nhau .

HĐ 4

Cho tam giác ABC như trong Hình 10a. Lấy một tờ giấy, trên đó vẽ tam giác A’B’C’có B’C’ = BC, \(\widehat {B'} = \widehat B\), \(\widehat {C'} = \widehat C\)theo các bước:

-Vẽ đoạn thẳng B’C’ = BC.

-Ở về cùng một phía của tờ giấy đối với đường thẳng B’C’vẽ \(\widehat {C'B'x} = \widehat {CBA}\), và vẽ \(\widehat {B'C'y} = \widehat {BCA}\).

-Vẽ giao điểm A’của hai tia B’x và C’y, ta được tam giác A’B’C’ (Hình 10b).

Em hãy cắt rời tam giác A’B’C’ra khỏi tờ giấy vừa vẽ và thử xem có thể đặt chồng khít tam giác A’B’C’lên tam giác ABC hay không.

Theo em, hai tam giác ABC và A’B’C’ trong trường hợp này có bằng nhau hay không?

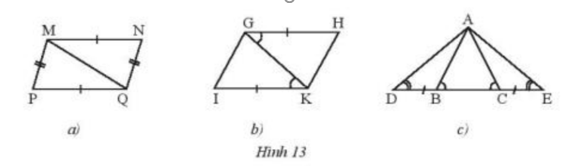
Phương pháp giải:

- Ta vẽ đoạn thẳng trước rồi từ 2 đầu đoạn thẳng lần lượt vẽ các góc theo số đo của tam giác ABC

- Sau khi cắt và chồng lên nhau sẽ thu được kết quả

Lời giải chi tiết:

Ta thấy 2 tam giác có thể chồng khít lên nhau nên 2 tam giác bằng nhau.

Từ đó ta suy ra 2 tam giác bằng nhau khi có 2 góc bằng nhau và cạnh xen giữa 2 góc đó cũng bằng nhau

Thực hành 2

Hãy chỉ ra các cặp tam giác bằng nhau trong Hình 13 và cho biết chúng bằng nhau theo trường hợp nào.

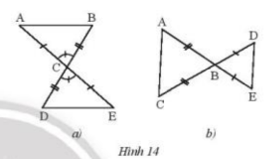
Phương pháp giải:

Dựa vào các trường hợp 2 tam giác bằng nhau c-c-c; c-g-c; g-c-g

Lời giải chi tiết:

a) Ta thấy tam giác MNQ = tam giác MPQ ( c-c-c )

b) Ta thấy tam giác GHK  = tam giác GIK ( c-g-c )

c) Ta thấy tam giác ADB = tam giác ACE ( g-c-g )

    Tam giác ADC = tam giác AEB ( g-c-g )

Thực hành 3

Hai tam giác trong mỗi hình bên (Hình 14a,b) có bằng nhau không? Vì sao?

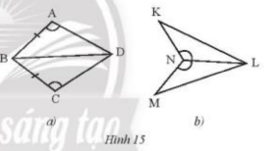
Phương pháp giải:

Sử dụng các trường hợp bằng nhau của tam giác: c-c-c;   c-g-c; g-c-g

Lời giải chi tiết:

a) Xét \(\Delta{ABC}\) và \(\Delta{EDC}\), ta có:

AC = CE

\(\widehat {ACB}\)= \(\widehat {DCE}\) ( 2 góc đối đỉnh )

CB = CD

\(\Rightarrow \Delta{ABC}=\Delta{EDC}\) (c.g.c)

b) Ta thấy 2 tam giác ABC và BDE không bằng nhau vì

\(AC \ne BE;BC \ne BD;DE \ne AC\)

Vận dụng 2

Nêu thêm điều kiện để hai tam giác trong mỗi hình bên (Hình 15a,b) bằng nhau theo trường hợp cạnh – góc – cạnh.

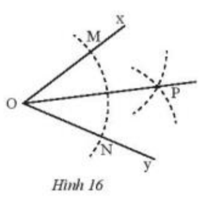
Phương pháp giải:

Dựa vào trường hợp cạnh – góc – cạnh

Lời giải chi tiết:

a) Theo trường hợp cạnh – góc – cạnh ta cần AD = CD để 2 tam giác bằng nhau

b) Theo trường hợp cạnh – góc – cạnh ta cần KN = MN để 2 tam giác bằng nhau

Vận dụng 3

Cho \(\widehat {xOy}\). Vẽ cung tròn tâm O, cung này cắt Ox, Oy theo thứ tự tại M, N. Vẽ hai cung tròn tâm M và tâm N có cùng bán kính sao cho chúng cắt nhau tại điểm P nằm trong \(\widehat {xOy}\). Nối O với P (Hình 16). Hãy chứng minh rằng , từ đó suy ra OP là tia phân giác của \(\widehat {xOy}\).

Phương pháp giải:

- Ta chứng minh 2 tam giác bằng nhau bằng phương pháp cạnh – cạnh – cạnh

Lời giải chi tiết:

Vì M, N thuộc đường tròn tâm O có cùng bán kính nên OM = ON = bán kính cung tròn tâm O

Từ M, N vẽ 2 cung tròn có cùng bán kính và 2 đường tròn cắt nhau tại P

Suy ra P thuộc cả 2 cung tròn tâm M, N có cùng bán kính nên MP = NP

Xét tam giác OMP và tam giác ONP ta có :

OM = ON

OP cạnh chung

MP =  NP

\(\Rightarrow \Delta{OMP}=\Delta{ONP}\) ( c-c-c )

\( \Rightarrow \widehat {MOP} = \widehat {PON}\) (2 góc tương ứng)

Do đó, OP là phân giác \(\widehat {xOy}\)