Bài 8.1, 8.2, 8.3 phần bài tập bổ sung trang 94, 95 SBT toán 6 tập 2Giải bài 8.1, 8.2, 8.3 phần bài tập bổ sung trang 94, 95 sách bài tập toán 6. Vẽ hình liên tiếp theo cách diễn đạt sau : a) Vẽ đoạn thẳng AB = 2cm. Vẽ đường tròn (c1) tâm A, bán kính AB ... Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
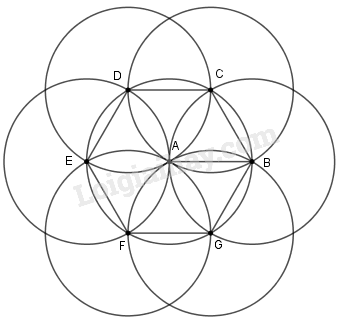
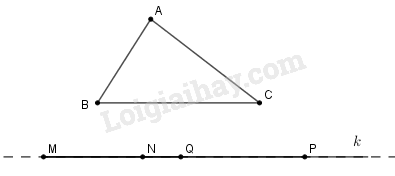
Bài 8.1 Vẽ hình liên tiếp theo cách diễn đạt sau : a) Vẽ đoạn thẳng \(AB = 2cm\). Vẽ đường tròn \((c1)\) tâm \(A\), bán kính \(AB\). b) Vẽ đường tròn \((c2)\) tâm \(B\), bán kính \(AB\). Gọi các giao điểm của đường tròn này với đường tròn \((c1)\) là \(C\) và \(G\). c) Vẽ đường tròn \((c3)\) tâm \(C\), bán kính \(AC\). Goi giao điểm mới củađường tròn này với đường tròn \((c1)\) là \(D\). d) Vẽ đường tròn \((c4)\) tâm \(D\), bán kính \(AD\). Gọi giao điểm mới của đường tròn này với đường tròn \((c1)\) là \(E\). e) Vẽ đường tròn \((c5)\) tâm \(E\), bán kính \(AE\). Gọi giao điểm mới của đường tròn này với đường tròn \((c1)\) là \(F\). f) Vẽ đường tròn \((c6)\) tâm \(F\), bán kính \(AF\). g) Vẽ đường tròn \((c7)\) tâm \(G\), bán kính \(AG\). Sau khi vẽ như trên hãy so sánh các đoạn thẳng: \(AB, BC, CD, DE, EF, FG, \)\(GB.\) Phương pháp giải: Vẽ hình theo yêu cầu bài toán, dùng thước thẳng hoặc compa để so sánh độ dài đoạn thẳng. Lời giải chi tiết: Sau khi vẽ ta được hình bs.17 Khi đó, các đoạn thẳng: \(AB, BC, CD, EF, FG, GB\) bằng nhau (vì cùng bằng bán kính 2cm) Bài 8.2 Vẽ đường tròn tâm \(O\), bán kính \(R = 3cm\).Vẽ một đường kính \(AB\). Vẽ tiếp một dây cung \(CD\) (hai điểm \(C, D\) không trùng với các điểm \(A,B\) và ba điểm \(C, O, D\) không thẳng hàng) a) Đọc tên các cung có các đầu mút là hai trong số các điểm \(A, B, C, D.\) b) So sánh độ dài của hai dây \(AB\) và \(CD.\) c) Nếu lấy \(n\) điểm (phân biệt) trên đường tròn đó ta có được bao nhiêu cung. Phương pháp giải: Cung của đường tròn là đoạn thẳng nối hai điểm phân biệt thuộc đường tròn. Lời giải chi tiết: Giả sử vẽ được như hình bs.18 a) Khi đó, có các cung là: \(AC\, nhỏ\), \(AD\) nhỏ, \(AB\) hay cung \(ACDB\), \(BA\) (cung nửa đường tròn không đi qua \(C\) và \(D\)) , \(ABD\) hay cung \(AD\) lớn, \(ABDC\) hay cung \(AC\) lớn, \(BD\) nhỏ, \(BC\) nhỏ, \(BAC\) hay cung \(BC\) lớn, \(BACD\) hay cung \(BD\) lớn, \(CD\) nhỏ, \(CABD\) hay \(CD\) lớn. b) Dùng compa so sánh được \(CD < AB\). c) Với hai điểm (phân biệt) trên một đường tròn ta có được hai cung có mút là hai điểm đó. Với \(n\) điểm (phân biệt) cho trước trên một đường tròn, thì cứ lấy \(2\) trong số \(n\) điểm đó ta được \(2\) cung, vì vậy có tất cả \(n(n – 1)\) cung trên đường tròn đó. Bài 8.3 Lấy ba điểm \(A, B, C\) bất kỳ, không thẳng hàng. Vẽ các đoạn thẳng \(AB, BC, CA\). a) Dùng compa để dựng đoạn \(MP = AB + BC\). b) Dùng compa để so sánh \(AC\) với \(AB + BC\). Phương pháp giải: Vẽ hình rồi dùng compa để so sánh Lời giải chi tiết: Vẽ đường thẳng \(k\) không cắt các đoạn thẳng \(AB, BC, CA\) (hình vẽ) Lấy một điểm \(M\) trên đường thẳng \(k\). a) Dùng compa dựng đoạn thẳng \(MN = AB\); dựng tiếp đoạn thẳng \(NP = BC\) (điểm \(N\) nằm giữa hai điểm \(M, P\)) Khi đó, ta có \(MP = AB + BC\). b) Tiếp tục, dùng compa dựng đoạn thẳng \(MQ = AC\). Khi đó thấy ngay điểm \(Q\) nằm giữa hai điểm \(M\) và \(P\) tức là \(MQ < MP\), từ đó suy ra \(AC < AB + BC\) Loigiaihay.com
|





















Danh sách bình luận