Bài 35 trang 93 SBT toán 6 tập 2

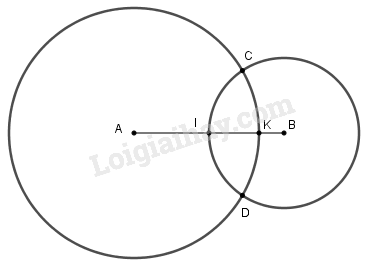
Đề bài

Cho hai điểm \(A,B\) cách nhau \(3cm\). Vẽ đường tròn \((A; 2,5cm)\) và đường tròn \((B; 1,5cm)\). Hai đường tròn này cắt nhau tại \(C\) và \(D\).

a) Tính \(CA, DB\).

b) Tại sao đường tròn \((B; 1,5cm)\) cắt đoạn thẳng \(AB\) tại trung điểm \(I\) của \(AB\)?

c) Đường tròn \((A; 2,5cm)\) cắt đoạn thẳng \(AB\) tại \(K\). Tính \(KB\).

Lời giải chi tiết

a) Vì \(C ∈ (A; 2,5cm)\) nên \(CA = 2,5cm.\) 

Vì \(D ∈ (B; 1,5cm)\) nên \(DB = 1,5 cm.\)

b)Vì đường tròn \((B; 1,5cm)\) cắt đoạn thẳng \(AB\) tại \(I\) nên \(I ∈ (B; 1,5cm)\) \(=>BI=1,5cm\)

Trên tia \(BI\) có \(BI<BA(1,5cm<3cm)\) nên \(I\) nằm giữa \(A\) và \(B\)

 Suy ra: \(AI + BI = AB\)

\( \Rightarrow \) \(AI = AB – BI = 3 – 1,5 = 1,5 (cm)\)

Do đó \(AI = IB (=1,5cm).\)

Vậy \(I\) là trung điểm của \(AB\).

c) Vì \(K\) nằm giữa \(A\) và \(B\) nên ta có \(AK + KB = AB\)

\( \Rightarrow \) \(KB = AB – AK \)\(= 3 – 2,5 = 0,5 (cm)\)

Loigiaihay.com