Giải bài 8 trang 75 vở thực hành Toán 7

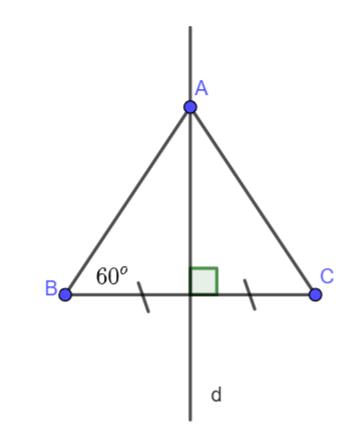
Đề bài

Bài 8. Cho điểm A nằm trên trung trực của đoạn thẳng BC sao cho \(\widehat {ABC} = {60^o}\). Chứng minh rằng CA = CB.

Lời giải chi tiết

GT	d là trung trực BC, \(A \in BC,\widehat {ABC} = {60^o}\)
KL	CA = CB.

Do A thuộc trung trực BC nên AB = AC hay  \(\Delta ABC\)cân tại A.

Từ đây suy ra \(\widehat {ACB} = \widehat {ABC} = {60^o}\). Do tổng ba góc trong tam giác ABC bằng \({180^o}\)nên:

\(\widehat {BAC} = {180^o} - \widehat {ACB} - \widehat {ABC} = {60^o}\)

Vậy tam giác ABC có ba góc bằng nhau nên ABC là tam giác đều và do đó CA = CB.