Giải Bài 7 trang 66 sách bài tập toán 7 - Chân trời sáng tạoCho tam giác ABC có ba đường phân giác AD, BE, CF đồng quy tại I. Vẽ IH vuông góc với BC tại H. Chứng minh rằng \(\widehat {BIH} = \widehat {CI{\rm{D}}}\). Tổng hợp đề thi học kì 1 lớp 7 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Khoa học tự nhiên... Quảng cáo
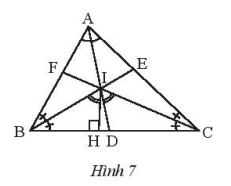
Đề bài Cho tam giác ABC có ba đường phân giác AD, BE, CF đồng quy tại I. Vẽ IH vuông góc với BC tại H. Chứng minh rằng \(\widehat {BIH} = \widehat {CI{\rm{D}}}\). Phương pháp giải - Xem chi tiết Sử dụng mối quan hệ giữa các góc trong tam giác để chứng minh Lời giải chi tiết
Ta có: \(\widehat {DIC} = {180^o} - \widehat {AIC} = \widehat {IAC} + \widehat {IC{\rm{A}}} = \frac{{\widehat {{A^{}}} + \widehat C}}{2}\) Ta có: \(\widehat {BIH} = {90^o} - \frac{{\widehat B}}{2} = \frac{{{{180}^o} - \widehat B}}{2} = \frac{{\widehat {{A^{}}} + \widehat C}}{2} = \widehat {DIC}\) Suy ra: \(\widehat {BIH} = \widehat {CI{\rm{D}}}\)  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
