Giải bài 4 (9.30) trang 83 vở thực hành Toán 7 tập 2Cho hai đường thẳng không vuông góc b, c cắt nhau tại điểm A và cho điểm H không thuộc b và c (H.9.36). Hãy tìm điểm B thuộc b, điểm C thuộc c sao cho tam giác ABC nhận H làm trực tâm. Quảng cáo
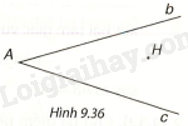
Đề bài Cho hai đường thẳng không vuông góc b, c cắt nhau tại điểm A và cho điểm H không thuộc b và c (H.9.36). Hãy tìm điểm B thuộc b, điểm C thuộc c sao cho tam giác ABC nhận H làm trực tâm.
Phương pháp giải - Xem chi tiết + Kẻ HJ\( \bot c\) cắt b tại B, kẻ \(HK \bot b\) cắt c tại C. + Chứng minh H là giao điểm của hai đường cao trong tam giác ABC. Lời giải chi tiết Kẻ HJ\( \bot c\) cắt b tại B; kẻ \(HK \bot b\) cắt c tại C. Khi đó tam giác ABC có hai đường cao BJ và CK cắt nhau tại H nên H là trực tâm của tam giác ABC.  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
