Giải bài 2 (9.28) trang 82 vở thực hành Toán 7 tập 2Xét điểm O cách đều ba đỉnh của tam giác ABC. Chứng minh rằng nếu O nằm trên một cạnh của tam giác ABC thì ABC là một tam giác vuông. Quảng cáo
Đề bài Xét điểm O cách đều ba đỉnh của tam giác ABC. Chứng minh rằng nếu O nằm trên một cạnh của tam giác ABC thì ABC là một tam giác vuông. Phương pháp giải - Xem chi tiết + Giả sử O là trung điểm của BC. + Chứng minh tam giác OAB cân tại O, tam giác OAC cân tại O, suy ra \(\widehat A = \widehat {{A_1}} + \widehat {{A_2}} = \widehat B + \widehat C\), mà \(\widehat A + \widehat B + \widehat C = {180^o}\), từ đó tính được \(\widehat A = {90^o}\). Lời giải chi tiết
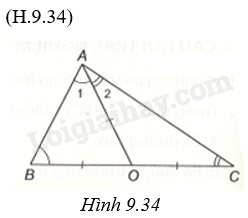
Giả sử điểm O nằm trên cạnh BC thì theo giả thiết, \(OB = OC\) nên O là trung điểm của BC. Từ giả thiết \(OA = OB = OC\) nên tam giác OAB cân tại O, tam giác OAC cân tại O. Vậy \(\widehat A = \widehat {{A_1}} + \widehat {{A_2}} = \widehat B + \widehat C\), mà \(\widehat A + \widehat B + \widehat C = {180^o}\), hay \(2\widehat A = {180^o}\), suy ra \(\widehat A = {90^o}\) hay tam giác ABC vuông tại A.  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
