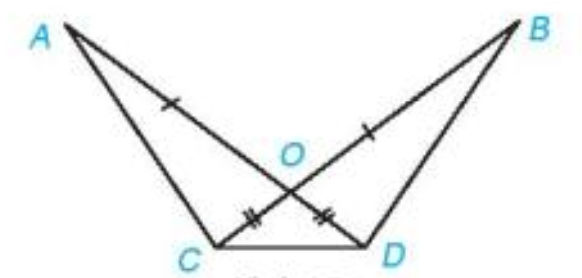
Giải bài 3 (4.31) trang 76 vở thực hành Toán 7

Đề bài

Bài 3 (4.31). Cho năm điểm A, B,C,D,O như hình vẽ. Biết rằng OA = OB, OC = OD.

 

a) Chứng minh rằng AC=BD.

b) Chứng minh rằng \(\Delta ACD = \Delta BDC\)

Lời giải chi tiết

a) Xét hai tam giác OAC và OBD ta có:

OA = OB (theo giả thiết)

\(\widehat {AOC} = \widehat {BOD}\)(hai góc đối đỉnh)

OC = OD (theo giả thiết)

Vậy \(\Delta OAC = \Delta OBD\)( c – g –c). Do đó AC = BD.

b) Xét hai tam giác ACD và BDC ta có:

AC = BD (chứng minh trên)

CD là cạnh chung

AD = AO + OD = BO + OC = BC

Vậy \(\Delta ACD = \Delta BDC\)( c-c-c)