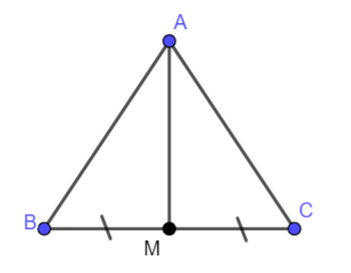
Giải bài 2 (4.24) trang 73 vở thực hành Toán 7

Đề bài

Bài 2 (4.24). Cho tam giác ABC cân tại A và M là trung điểm của BC. Chứng minh AM vuông góc với BC và AM là tia phân giác của góc BAC.

Lời giải chi tiết

GT	\(\Delta ABC\)cân tại A, \(M \in BC,MB = MC.\)
KL	\(AM \bot BC,\widehat {MAB} = \widehat {MAC}\)

Xét tam giác ABM và ACM ta có:

AB = AC (do \(\Delta ABC\)cân tại A)

\(\widehat {ABM} = \widehat {ACM}\) (do \(\Delta ABC\)cân tại A)

MB = MC (theo giả thiết)

Vậy \(\Delta ABM = \Delta ACM\)(c – g – c). Do đó \(\widehat {MAB} = \widehat {MAC}\) hay AM là tia phân giác của góc BAC.

Đồng thời  \(\widehat {AMB} = \widehat {AMC} = \frac{{\widehat {AMB} + \widehat {AMC}}}{2} = \frac{{{{180}^o}}}{2} = {90^o}\) hay \(AM \bot BC.\)