Giải bài 8 trang 81 vở thực hành Toán 7

Đề bài

Bài 8. Tam giác ABC vuông tại đỉnh A và có \(\widehat B = {30^o}\). Chứng minh rằng BC = 2AC

Lời giải chi tiết

GT	\(\Delta ABC\)vuông tại A, \(\widehat B = {30^o}\)
KL	BC = 2AC

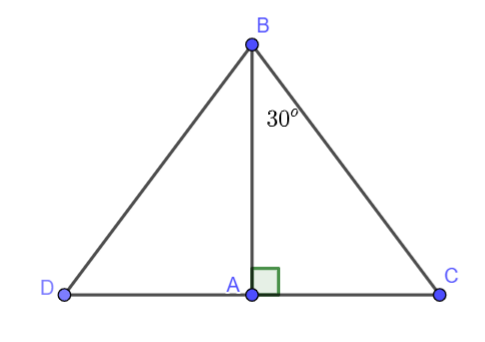
Trên tia đối của tia AC lấy điểm D sao cho AD = AC.

Tam giác ACB và tam giác ADB vuông tại A và có:

AB là cạnh chung

AC = AD (theo cách dựng)

Vậy \(\Delta ACB = \Delta ADB\)(hai cạnh góc vuông). Do đó BC = BD

Vậy tam giác BCD cân tại B. Suy ra \(\widehat {ABD} = \widehat {ABC} = {30^o}\)

Như vậy:

\(\begin{array}{l}\widehat {CBD} = \widehat {ABC} + \widehat {ABD} = {60^o}\\\widehat {CDB} = \widehat {DCB} = \frac{{{{180}^o} - {{60}^o}}}{2} = {60^o}\end{array}\)

Do vậy ABD là tam giác đều. Do đó BC = DC = 2AC