Giải bài 7 trang 54, 55 vở thực hành Toán 7 tập 2a) Tìm đa thức A, biết rằng (left( {4{x^2} + 9} right).A = 16{x^4} - 81). b) Tìm đa thức M sao cho (left( {27{x^3} + 8} right):M = 3x + 2). Quảng cáo
Đề bài a) Tìm đa thức A, biết rằng \(\left( {4{x^2} + 9} \right).A = 16{x^4} - 81\). b) Tìm đa thức M sao cho \(\left( {27{x^3} + 8} \right):M = 3x + 2\). Phương pháp giải - Xem chi tiết a) Vì \(\left( {4{x^2} + 9} \right).A = 16{x^4} - 81\) nên \(A = \left( {6{x^4} - 81} \right):\left( {4{x^2} + 9} \right)\), từ đó tìm được A. b) Vì \(\left( {27{x^3} + 8} \right):M = 3x + 2\) nên \(M = \left( {27{x^3} + 8} \right):\left( {3x + 2} \right)\), từ đó tìm được M. Lời giải chi tiết a) Để có \(\left( {4{x^2} + 9} \right).A = 16{x^4} - 81\), phép chia \(\left( {6{x^4} - 81} \right):\left( {4{x^2} + 9} \right)\) phải là phép chia hết và A là đa thức thương. Ta đặt tính chia như sau:
Vậy \(A = 4{x^2} - 9\) b) Đa thức M thỏa mãn đẳng thức \(\left( {27{x^3} + 8} \right):M = 3x + 2\) chính là thương của phép chia \(\left( {27{x^3} + 8} \right):\left( {3x + 2} \right)\), với điều kiện đó là phép chia hết. Ta đặt tính chia như sau:
Vậy \(M = 9{x^2} - 6x + 4\).
|














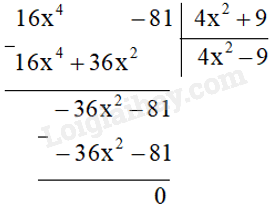
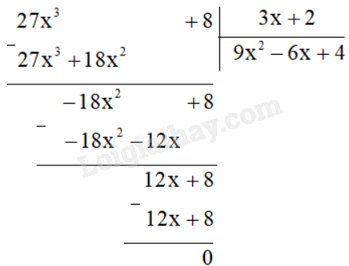






Danh sách bình luận