Giải Bài 5 trang 49 sách bài tập toán 7 - Chân trời sáng tạo

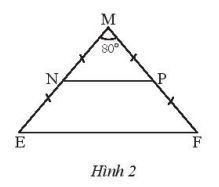
Đề bài

Cho tam giác MEF cân tại M, có \(\widehat M = {80^o}\)

a) Tính \(\widehat E{,^{}}\widehat F\)

b) Gọi N, P lần lượt là trung điểm của ME, MF. Chứng minh rằng tam giác MNP cân.

c) Chứng minh rằng NP // EF

Lời giải chi tiết

a) Vì tam giác MEF cân tại M nên \(\widehat E = \widehat F = \frac{{{{180}^o} - {{80}^o}}}{2} = {50^o}\)

b) Ta có tam giác MEF cân tại M do đó ME = MF.

Suy ra: \(MN = \frac{{ME}}{2} = \frac{{MF}}{2} = MP\)

Vậy tam giác MNP cân tại M.

c) Trong tam giác cân MNP ta có: \(\widehat N = \widehat P = \frac{{{{180}^o} - {{80}^o}}}{2} = {50^o}\)

nên \(\widehat {MNP} = \widehat {{\rm{NEF}}} = {50^o}\)

Suy ra NP // EF (vì hai góc đồng vị bằng nhau)