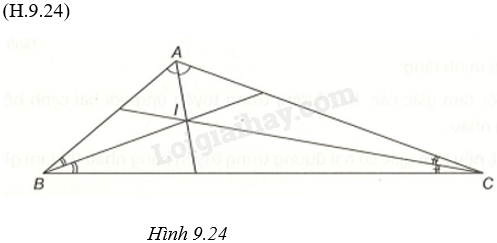
Giải bài 4 (9.23) trang 78 vở thực hành Toán 7 tập 2Kí hiệu I là điểm đồng quy của ba đường phân giác trong tam giác ABC. Tính góc BIC khi biết góc BAC bằng 120o. Quảng cáo
Đề bài Kí hiệu I là điểm đồng quy của ba đường phân giác trong tam giác ABC. Tính góc BIC khi biết góc BAC bằng 120o. Phương pháp giải - Xem chi tiết + Chỉ ra \(\widehat {IBC} = \frac{{\widehat B}}{2},\widehat {ICB} = \frac{{\widehat {ACB}}}{2}\) \(\widehat {BIC} = {180^o} - \left( {\frac{{\widehat B}}{2} + \frac{{\widehat {ACB}}}{2}} \right)\), \(\frac{{\widehat B}}{2} + \frac{{\widehat C}}{2} = \frac{{\widehat B + \widehat C}}{2} = {30^o}\), nên tính được góc \(\widehat{BIC}\). Lời giải chi tiết
Xét \(\Delta ABC\) có I là giao điểm của ba đường phân giác nên: mà \(\frac{{\widehat {ABC}}}{2} + \frac{{\widehat {ACB}}}{2} = \frac{{\widehat {ABC} + \widehat {ACB}}}{2} = \frac{{{{180}^o} - \widehat {BAC}}}{2} = \frac{{{{180}^o} - {{120}^o}}}{2} = {30^o}\) Do đó, \(\widehat {BIC} = {180^o} - {30^o} = {150^o}\).  Chia sẻ Bình luận
Tham Gia Group Dành Cho Lớp 7 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
Danh sách bình luận