Giải bài 2 (9.21) trang 77, 78 vở thực hành Toán 7 tập 2

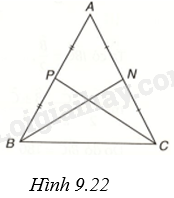
Đề bài

Chứng minh rằng:

a) Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên là hai đoạn thẳng bằng nhau.

b) Ngược lại, nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.

Lời giải chi tiết

(H.9.22)

a) Tam giác ABC cân tại A và có BN, CP là hai đường trung tuyến. Ta cần chứng minh \(BN = CP\).

Tam giác ABC cân tại A nên \(AB = AC\).

Do N, P lần lượt là trung điểm của AC, AB nên \(BP = \frac{1}{2}AB,CN = \frac{1}{2}AC\), do đó \(BP = CN\).

Xét hai tam giác BCP và CBN, ta có:

\(BP = CN\), \(\widehat {BPC} = \widehat {NCB}\), BC chung nên \(\Delta BCP = \Delta CBN\left( {c.g.c} \right)\).

Suy ra \(CP = BN\).

b) BN, CP là hai đường trung tuyến của tam giác ABC, \(BN = CP\). Ta sẽ chứng minh \(AB = AC\).

Gọi G là trọng tâm của tam giác ABC.

Xét hai tam giác PGB và NGC, ta có:

\(PG = NG,BG = GC,\widehat {PGB} = \widehat {NGC}\) (đối đỉnh)

Vậy \(\Delta PGB = \Delta NGC\left( {c.g.c} \right)\), suy ra \(BP = NC\).

Do đó, \(AB = 2BP = 2CN = AC\)

Vậy tam giác ABC cân tại A.