Bài 11.5, 11.6, 11.7 phần bài tập bổ sung trang 28 SBT toán 6 tập 2Giải bài 11.5, 11.6, 11.7 phần bài tập bổ sung trang 28 sách bài tập toán 6. Tính giá trị của biểu thức ... Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Bài 11.5* Tính tích \(\displaystyle A = {3 \over 4}.{8 \over 9}.{{15} \over {16}}...{{899} \over {900}}\) Phương pháp giải: Phân tích tử số và mẫu số thành tích của các thừa số, sau đó cùng chia cả tử và mẫu cho các thừa số chung. Lời giải chi tiết: \(\displaystyle {\rm{A}} = {{1.3} \over {2.2}}.{{2.4} \over {3.3}}.{{3.5} \over {4.4}}...{{29.31} \over {30.30}}\) \(\displaystyle A= {{1.2.3...29} \over {2.3.4...30}}.{{3.4.5...31} \over {2.3.4...30}}\) \(\displaystyle A = {1 \over {30}}.{{31} \over 2} = {{31} \over {60}}\) Bài 11.6* Chứng tỏ rằng \(\displaystyle {1 \over 5} + {1 \over 6} + {1 \over 7} + ... + {1 \over {17}} < 2\) Phương pháp giải: - So sánh các phân số \(\displaystyle {1 \over 5} ; {1 \over 6} \; {1 \over 7};{1 \over 8} \; {1 \over 9}\) với phân số \(\displaystyle {1 \over 5}.\) - So sánh các phân số \(\displaystyle {1 \over 10} ; {1 \over 11} \;... \; ;{1 \over 17}\) với phân số \(\displaystyle {1 \over 8}.\) Lời giải chi tiết: Ta có: \(\dfrac{1}{6} < \dfrac{1}{5},\dfrac{1}{7} < \dfrac{1}{5},\)\(\dfrac{1}{8} < \dfrac{1}{5},\dfrac{1}{9} < \dfrac{1}{5}\) \( \Rightarrow \displaystyle {1 \over 5} + {1 \over 6} + {1 \over 7} + {1 \over 8} + {1 \over 9}\)\( < \displaystyle {1 \over 5} + {1 \over 5} + {1 \over 5} + {1 \over 5} + {1 \over 5}\) \(\Rightarrow \displaystyle {1 \over 5} + {1 \over 6} + {1 \over 7} + {1 \over 8} + {1 \over 9} < {1 \over 5}.5 = 1\) \(\Rightarrow \displaystyle {1 \over 5} + {1 \over 6} + {1 \over 7} + {1 \over 8} + {1 \over 9} < 1\) \((1)\) Lại có: \(\dfrac{1}{{10}} < \dfrac{1}{8},\dfrac{1}{{11}} < \dfrac{1}{8},...,\dfrac{1}{{17}} < \dfrac{1}{8}\) \( \Rightarrow \displaystyle {1 \over {10}} + {1 \over {11}} + ... + {1 \over {16}} + {1 \over {17}} \)\( < \displaystyle {1 \over 8} + {1 \over 8} + ... + {1 \over 8} + {1 \over 8}\) \(\Rightarrow \displaystyle {1 \over {10}} + {1 \over {11}} + ... + {1 \over {16}} + {1 \over {17}} < {1 \over 8}.8 \) \(\Rightarrow \displaystyle {1 \over {10}} + {1 \over {11}} + ... + {1 \over {16}} + {1 \over {17}} < 1\) \((2)\) Cộng theo từng vế \((1)\) và \((2)\) ta được: \(\displaystyle {1 \over 5} + {1 \over 6} + ... + {1 \over {17}} < 2.\) Bài 11.7* Tính giá trị của biểu thức : \(\displaystyle M = {1 \over {1.2.3}} + {1 \over {2.3.4}} + {1 \over {3.4.5}} + ... \)\(\displaystyle + {1 \over {10.11.12}}\) Phương pháp giải: Ta có nhận xét ; \(\displaystyle {1 \over {1.2}} - {1 \over {2.3}} = {{3 - 1} \over {1.2.3}} = {2 \over {1.2.3}};\) \(\displaystyle {1 \over {2.3}} - {1 \over {3.4}} = {{4 - 2} \over {2.3.4}} = {2 \over {2.3.4}};...\) Suy ra: \(\displaystyle {1 \over {1.2.3}} = {1 \over 2}.\left( {{1 \over {1.2}} - {1 \over {2.3}}} \right)\) \(\displaystyle {1 \over {2.3.4}} = {1 \over 2}.\left( {{1 \over {2.3}} - {1 \over {3.4}}} \right);...\) Ta tiếp tục là tương tự với các phân số còn lại, từ đó tính được tổng \(M.\) Lời giải chi tiết:
Loigiaihay.com
|














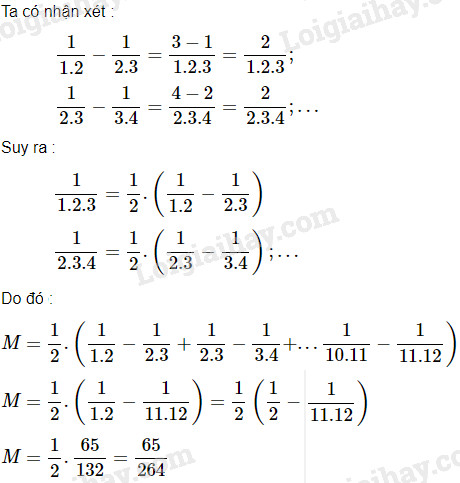






Danh sách bình luận