Bài 62 trang 17 SBT toán 6 tập 2Giải bài 62 trang 17 sách bài tập toán 6. Hoàn thành các bảng sau : ... Quảng cáo
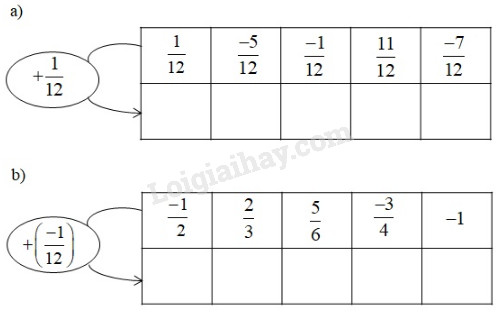
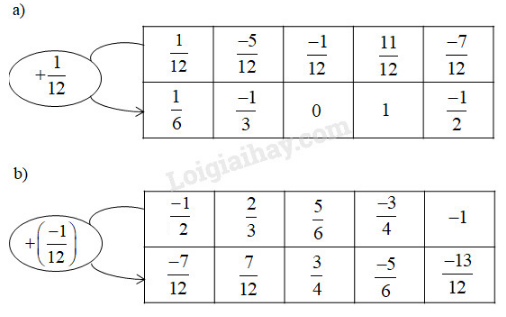
Đề bài Hoàn thành các bảng sau:
Phương pháp giải - Xem chi tiết Ta làm như sau: - Lần lượt cộng các phân số ở hàng trên với phân số ở trong hình tròn. - Muốn cộng hai phân số cùng mẫu số, ta cộng các tử và giữ nguyên mẫu. - Muốn cộng hai phân số không cùng mẫu, ta viết dưới dạng hai phân số có cùng một mẫu rồi cộng các tử và giữ nguyên mẫu chung. Lời giải chi tiết
Giải thích: \(\begin{array}{l} \(b)\dfrac{{ - 1}}{{12}} + \dfrac{{ - 1}}{2} = \dfrac{{ - 1}}{{12}} + \dfrac{{ - 6}}{{12}} \)\(= \dfrac{{ - 1 + \left( { - 6} \right)}}{{12}} = \dfrac{{ - 7}}{{12}}\) \(\dfrac{{ - 1}}{{12}} + \dfrac{2}{3} = \dfrac{{ - 1}}{{12}} + \dfrac{8}{{12}} \)\(= \dfrac{{\left( { - 1} \right) + 8}}{{12}} = \dfrac{7}{{12}}\) \(\dfrac{{ - 1}}{{12}} + \dfrac{5}{6} = \dfrac{{ - 1}}{{12}} + \dfrac{{10}}{{12}} \)\(= \dfrac{{ - 1 + 10}}{{12}} = \dfrac{9}{{12}} = \dfrac{3}{4}\) \(\dfrac{{ - 1}}{{12}} + \dfrac{-3}{4} = \dfrac{{ - 1}}{{12}} + \dfrac{{-9}}{{12}} \)\(= \dfrac{{( - 1) + (-9)}}{{12}} = \dfrac{-10}{{12}} = \dfrac{-5}{6}\) \(\dfrac{{ - 1}}{{12}} +(-1) = \dfrac{{ - 1}}{{12}} + \dfrac{-12}{{12}} \)\(= \dfrac{{\left( { - 1} \right) + (-12)}}{{12}} = \dfrac{-13}{{12}}\) Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K13 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
