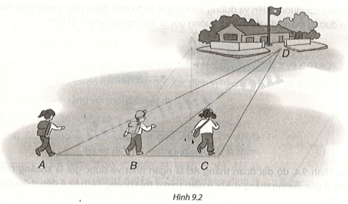
Giải bài 4 (9.4) trang 67, 68 vở thực hành Toán 7 tập 2

Đề bài

Ba bạn Mai, Việt và Hà đi đến trường tại địa điểm D lần lượt theo ba con đường AD, BD và CD (H.9.2). Biết rằng ba điểm A, B, C cùng nằm trên một đường thẳng, B nằm giữa A và C, \(\widehat {ACD}\) là góc tù. Hỏi bạn nào đi xa nhất, bạn nào đi gần nhất? Vì sao?

Lời giải chi tiết

Trong tam giác BDC có \(\widehat {ACD}\) là góc tù. Cạnh BD đối diện \(\widehat {ACD}\) nên BD là cạnh lớn nhất, suy ra \(BD > DC\). (1)

Tương tự, trong tam giác ABD có \(\widehat {ABD}\) là góc tù (vì \(\widehat {ABD}\) kề bù với góc nhọn \(\widehat {DBC}\)), cạnh AD đối diện với \(\widehat {ABD}\), suy ra \(AD > BD\). (2)

Từ (1) và (2), ta có \(AD > BD > DC\). Vậy bạn Mai đi xa nhất và bạn Hà đi gần nhất.