Giải bài 4 (9.39) trang 88 vở thực hành Toán 7 tập 2Cho tam giác ABC có đường phân giác AD, D nằm trên BC sao cho (BD = 2DC). Trên đường thẳng AC, lấy điểm E sao cho C là trung điểm của AE (H.9.47). Chứng minh rằng tam giác ABE cân tại A. Gợi ý. D là trọng tâm của tam giác ABE, tam giác này có đường phân giác AD đồng thời là đường trung tuyến. Quảng cáo
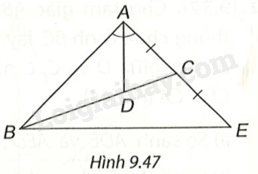
Đề bài Cho tam giác ABC có đường phân giác AD, D nằm trên BC sao cho \(BD = 2DC\). Trên đường thẳng AC, lấy điểm E sao cho C là trung điểm của AE (H.9.47). Chứng minh rằng tam giác ABE cân tại A. Gợi ý. D là trọng tâm của tam giác ABE, tam giác này có đường phân giác AD đồng thời là đường trung tuyến. Phương pháp giải - Xem chi tiết + Chứng minh D là trọng tâm tam giác ABE, suy ra AD là đường trung tuyến của tam giác ABE. + Vì AD là đường phân giác đồng thời là đường trung tuyến trong tam giác ABE nên tam giác ABE cân tại A. Lời giải chi tiết Trong tam giác ABE có BC là đường trung tuyến, mà \(BD = 2DC\) nên D là trọng tâm của tam giác ABE. Vậy AD phải là đường trung tuyến của tam giác ABE. Trong tam giác ABE có AD là đường phân giác đồng thời là đường trung tuyến nên tam giác ABE cân tại A.
|




















Danh sách bình luận