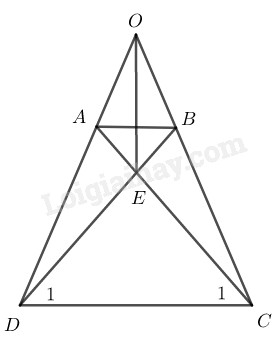
Bài 31 trang 83 SBT toán 8 tập 1

Đề bài

Hình thang cân \(ABCD\) có \(O\) là giao điểm của hai đường thẳng chứa cạnh bên \(AD,\) \(BC\) và \(E\) là giao điểm của hai đường chéo. Chứng minh rằng \(OE\) là đường trung trực của hai đáy.

Lời giải chi tiết

Vì ABCD là hình thang cân nên: 

\(\eqalign{
& \widehat {ADC} = \widehat {BCD} \cr 
& \Rightarrow \widehat {ODC} = \widehat {OCD} \cr} \) 

\(⇒ ∆ OCD\) cân tại \(O\)

\(⇒ OC = OD\)

\(⇒ OA + AD = OB + BC\)

Mà \(AD = BC\) (tính chất hình thang cân)

\(⇒ OA = OB\)

Xét \(∆ ADC\) và \(∆ BCD :\)

\(AD = BC\) (chứng minh trên)

\(AC = BD\) (tính chất hình thang cân)

\(CD\) cạnh chung

Do đó: \(∆ ADC = ∆ BCD\;\;\; (c.c.c)\)

\( \Rightarrow {\widehat D_1} = {\widehat C_1}\)

\(⇒ ∆ EDC\) cân tại \(E\)

\(⇒ EC = ED\) nên \(E\) thuộc đường trung trực của \(CD\)

\(OC = OD\) nên \(O\) thuộc đường trung trực của \(CD\)

\(E≢ O.\) Vậy \(OE\) là đường trung trực của \(CD.\)

\(BD = AC\) (tính chất hình thang cân)

\(⇒ EB + ED = EA + EC\) mà \(ED = EC\)  (chứng minh trên)

\(⇒ EB = EA\) \(\Rightarrow \Delta EAB\) cân tại \(E\)

nên \(E\) thuộc đường trung trực \(AB\)

\( OA = OB\) ( chứng minh trên) \(\Rightarrow \Delta OAB\) cân tại \(O\)

nên \(O\) thuộc đường trung trực \(AB\)

\(E≢ O.\) Vậy \(OE\) là đường trung trực của \(AB.\)

Loigiaihay.com