Bài 30 trang 83 SBT toán 8 tập 1

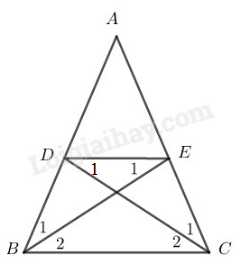
LG a

\(\) Tứ giác \(BDEC\) là hình gì \(?\) Vì sao \(?\)

Phương pháp giải:

Ta sử dụng kiến thức:

+) Hình thang là tứ giác có hai cạnh đối song song.

+) Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.

Lời giải chi tiết:

Ta có: \(AD = AE \;\;\; (gt)\) 

\(⇒ ∆ ADE\) cân tại \(A\)

\( \Rightarrow \widehat {ADE} = \displaystyle {{{{180}^0} - \widehat A} \over 2}\) 

\(∆ ABC\) cân tại \(A\)

\( \Rightarrow \widehat {ABC} = \displaystyle {{{{180}^0} - \widehat A} \over 2}\) 

Suy ra:  \(\widehat {ADE} = \widehat {ABC}\)

\(⇒ DE // BC\) (vì có cặp góc đồng vị bằng nhau)

Tứ giác \(BDEC\) là hình thang

\(\widehat {ABC} = \widehat {ACB}\) (tính chất tam giác cân)

Hay \(\widehat {DBC} = \widehat {ECB}\). Vậy BDEC là hình thang cân

LG b

\(\) Các điểm \(D,\) \(E\) ở vị trí nào thì \(BD = DE = EC\) \(?\)

Phương pháp giải:

Ta sử dụng kiến thức:

+) Hình thang là tứ giác có hai cạnh đối song song.

+) Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.

Lời giải chi tiết:

\(\) Giả sử: \(BD = DE\) \(⇒ ∆ BDE\) cân tại \(D\)

\( \Rightarrow {\widehat B_1} = {\widehat E_1}\)

Mà \({\widehat E_1} = {\widehat B_2}\) (so le trong)

\( \Rightarrow {\widehat B_1} = {\widehat B_2}\)

\(\Rightarrow BE\) là tia phân giác của \(\widehat {ABC}.\)

Giả sử: \(DE = EC\) \(⇒∆ DEC\) cân tại \(E\)

\( \Rightarrow {\widehat D_1} = {\widehat C_1}\)

\({\widehat D_1} = {\widehat C_2}\) (so le trong)

\( \Rightarrow {\widehat C_1} = {\widehat C_2}\)

\(\Rightarrow CD\) là tia phân giác của \(\widehat {ACB}.\)

Vậy khi \(BE\) là tia phân giác của \(\widehat {ABC}\), \(CD\) là tia phân giác của \(\widehat {ACB}\) thì \(BD = DE = EC.\)

Loigiaihay.com