Bài 29 trang 89 SBT toán 6 tập 2

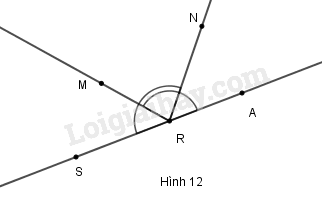
Đề bài

a) Vẽ vào vở hình 12 trong đó ba điểm \(S, R, A\) thẳng hàng và \(\widehat {{\rm{AR}}M} = \widehat {S{\rm{R}}N} = {130^\circ}\)

b) Tính \(\widehat {{\rm{AR}}N},\widehat {M{\rm{RS}}},\widehat {M{\rm{R}}N}\)

c) Dùng thước đo góc kiểm tra lại kết quả. 

Lời giải chi tiết

a) Ta có hình vẽ

b) Vì \(\widehat {{{AR}}N}\) và \(\widehat {S{{RN}}}\) kề bù nên :

\(\widehat {{{AR}}N} + \widehat {S{{R}}N} = {180^\circ}\)

Thay \(\widehat {S{{RN}}} = {130^\circ}\) ta có :

\(\widehat {{{AR}}N} + {130^\circ} = {180^\circ}\)

\( \Rightarrow \widehat {{\rm{AR}}N} = {180^\circ} - {130^\circ} = {50^\circ}\)

Vì \(\widehat {{{AR}}M}\) và \(\widehat {M{{RS}}}\) kề bù nên :

\(\widehat {{{AR}}M} + \widehat {M{{RS}}} = {180^\circ}\)

Thay \(\widehat {{{AR}}M} = {130^\circ}\) ta có :

\({130^\circ} + \widehat {M{{RS}}} = {180^\circ}\)

\( \Rightarrow \widehat {M{{RS}}} = {180^\circ} - {130^\circ} = {50^\circ}\)

Trên cùng một nửa mặt phẳng bờ chứa tia \(RA\) ta có : \(\widehat {{{AR}}N} = {50^\circ};\widehat {{{AR}}M} = {130^\circ}\) suy ra \(\widehat {{{AR}}N} < \widehat {{{AR}}M}\)

\(\Rightarrow\)  Tia \(RN\) nằm giữa hai tia \(RA\) và \(RM\)

\(\Rightarrow \widehat {{{AR}}N} + \widehat {M{{R}}N} = \widehat {{{AR}}M}\). Thay \(\widehat {{{AR}}N} = {50^\circ};\widehat {{{AR}}M} = {130^\circ}\) ta có :

\({50^\circ} + \widehat {M{{R}}N} = {130^\circ}\)

\( \Rightarrow \widehat {M{{R}}N} = {130^\circ} - {50^\circ} = {80^\circ}\)

c) Dùng thước đo góc kiểm tra lại. Ta đo được: \( \widehat {{\rm{AR}}N} =50^0,  \widehat {{\rm{MR}}S} =50^0, \widehat {{\rm{MR}}N} =80^0\) 

Loigiaihay.com