Giải bài 2 (6.23) trang 17 vở thực hành Toán 7 tập 2Theo bảng giá trị dưới đây, hai đại lượng x và y có phải là hai đại lượng tỉ lệ nghịch không? Quảng cáo
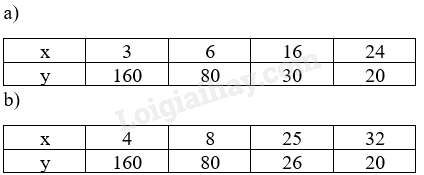
Đề bài Theo bảng giá trị dưới đây, hai đại lượng x và y có phải là hai đại lượng tỉ lệ nghịch không?
Phương pháp giải - Xem chi tiết a) Nếu đại lượng y liên hệ với đại lượng x theo công thức \(xy = a\) (a là hằng số khác 0) thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ a. b) Kiểm tra tích hai giá trị tương ứng của x và y. + Nếu thu được các tích bằng nhau thì đó là đại lượng tỉ lệ nghịch. + Nếu các tích thu được không bằng nhau thì đó không là hai đại lượng tỉ lệ nghịch. Lời giải chi tiết a) Dễ thấy \(xy = 480\) hay \(y = \frac{{480}}{x}\) nên x và y là hai đại lượng tỉ lệ nghịch. b) Với \(x = 25,y = 26\) thì ta có \(xy = 25.26 = 650\), khác với các tích xy khác (bằng 640), nên x và y không là hai đại lượng tỉ lệ nghịch.
|




















Danh sách bình luận