Trắc nghiệm Bài 5: Đường trung trực của một đoạn thẳng Toán 7 Chân trời sáng tạoĐề bài
Câu 1 :
Cho d là đường trung trực của đoạn thẳng AB. Gọi O là trung điểm của AB. Trên d lấy 2 điểm M, N sao cho OM = ON. Tứ giác AMBN là hình gì? Chọn câu trả lời đúng nhất.
Câu 2 :
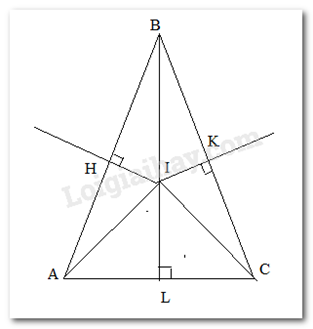
Cho tam giác ABC cân tại B. Kẻ đường trung trực của BA cắt AB tại H, trung trực của BC cắt BC tại K và trung trực của AC cắt AC tại L. 3 đường trung trực này cắt nhau tại I.
Lời giải và đáp án
Câu 1 :
Cho d là đường trung trực của đoạn thẳng AB. Gọi O là trung điểm của AB. Trên d lấy 2 điểm M, N sao cho OM = ON. Tứ giác AMBN là hình gì? Chọn câu trả lời đúng nhất.
Đáp án : C Phương pháp giải :
Sử dụng tính chất đường trung trực của đoạn thẳng. Áp dụng các trường hợp bằng nhau của tam giác suy ra các cạnh bằng nhau. Lời giải chi tiết :
Vì M nằm trên đường trung trực của AB nên MA = MB ( tính chất) Vì N nằm trên đường trung trực của AB nên NA = NB ( tính chất) Xét tam giác AOM và AON có: OM = ON \(\widehat {AOM} = \widehat {AON}( = 90^\circ )\) AO chung \( \Rightarrow \Delta AOM = \Delta AON\) ( c.g.c) \( \Rightarrow \) AM = AN ( 2 cạnh tương ứng) Mà MA = MB; NA = NB \( \Rightarrow \) MA = MB = NB = NA \( \Rightarrow \) Tứ giác AMBN là hình thoi ( Tứ giác có 4 cạnh bằng nhau)
Câu 2 :
Cho tam giác ABC cân tại B. Kẻ đường trung trực của BA cắt AB tại H, trung trực của BC cắt BC tại K và trung trực của AC cắt AC tại L. 3 đường trung trực này cắt nhau tại I.
Đáp án : A Phương pháp giải :
Dựa vào tính chất tam giác cân Lời giải chi tiết :
Vì tam giác ABC cân tại B nên BA = BC Mà H, K lần lượt là trung điểm của BA và BC nên BH = BK Xét tam giác vuộng BHI và BKI có: BI chung BH = BK \( \Rightarrow BHI = \Delta BKI\) ( cạnh huyền – cạnh góc vuông) \( \Rightarrow \) IH = IK (hai cạnh tương ứng).
|
