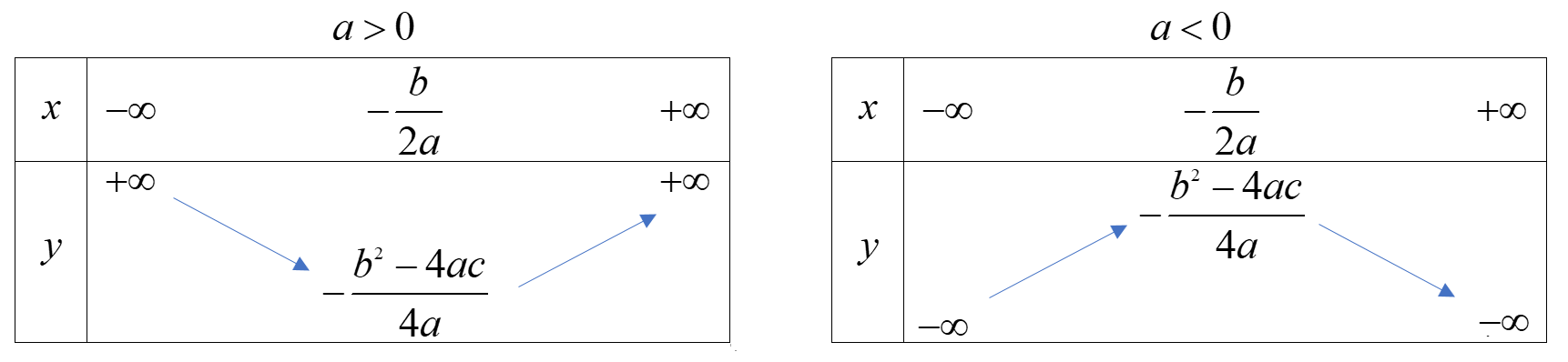
Sự biến thiên của hàm số bậc hai.(a > 0) Hàm số nghịch biến trên (( - infty ; - frac{b}{{2a}})), đồng biến trên (( - frac{b}{{2a}}; + infty )) Quảng cáo
1. Lý thuyết Cho hàm số \(y = a{x^2} + bx + c\;(a \ne 0)\)
+ Bảng biến thiên
+ Chú ý Từ bảng biến thiên, ta thấy Khi \(a > 0\), hàm số đạt giá trị nhỏ nhất bằng \( - \frac{{{b^2} - 4ac}}{{4a}}\) tại \(x = - \frac{b}{{2a}}\) và hàm số có tập giá trị là \([ - \frac{{{b^2} - 4ac}}{{4a}}; + \infty )\) Khi \(a < 0\), hàm số đạt giá trị lớn nhất bằng \( - \frac{{{b^2} - 4ac}}{{4a}}\) tại \(x = - \frac{b}{{2a}}\) và hàm số có tập giá trị là \(( - \infty ; - \frac{{{b^2} - 4ac}}{{4a}}]\)
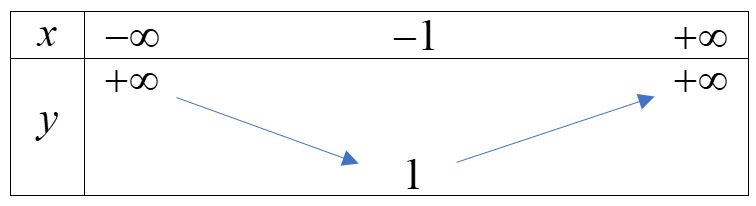
2. Ví dụ minh họa Ví dụ 1. Xét sự biến thiên của hàm số \(y = {x^2} + 2x + 2\) Hàm số \(y = {x^2} + 2x + 2\) có \(a = 1,b = 2,c = 2\) \( \Rightarrow - \frac{b}{{2a}} = - \frac{2}{{2.1}} = - 1;y( - 1) = {( - 1)^2} + 2.( - 1) + 2 = 1\) Bảng biến thiên Hàm số đồng biến trên \(( - 1; + \infty )\), nghịch biến trên \(( - \infty ; - 1)\)
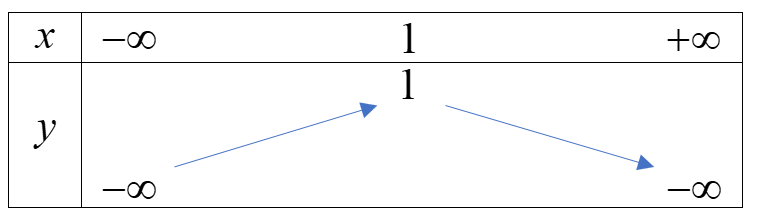
Ví dụ 2. Lập bảng biến thiên và tìm khoảng đồng biến, nghịch biến của hàm số \(y = - {x^2} + 2x\) Hàm số \(y = - {x^2} + 2x\) có \(a = - 1,b = 2,c = 0\) \( \Rightarrow - \frac{b}{{2a}} = - \frac{2}{{2.( - 1)}} = 1;y(1) = - {1^2} + 2.1 = 1\) Bảng biến thiên
Hàm số đồng biến trên \(( - \infty ;1)\), nghịch biến trên \((1; + \infty )\)
|




















Danh sách bình luận